cs231n 강의 노트 6장 Neural Networks Part 2: Setting up the Data and the Loss

cs231n 강의 노트 6장 Neural Networks Part 2: Setting up the Data and the Loss

1.Setting up the data and the model

In the previous section we introduced a model of a Neuron, which computes a dot product following a non-linearity, and Neural Networks that arrange neurons into layers.
Together, these choices define the new form of the score function, which we have extended from the simple linear mapping that we have seen in the Linear Classification section.
In particular, a Neural Network performs a sequence of linear mappings with interwoven non-linearities.
In this section we will discuss additional design choices regarding data preprocessing, weight initialization, and loss functions.

• 이전 섹션에서 우리는 비선형성에 따라 내적을 계산하는 뉴런 모델과 신경망를 배열로 나타내는 신경망을 소개했습니다.
• 이전에서 배웠던 Linear Classification section를 통해 score 함수를 확장하여 정의할 것이다.
• 특히, 신경망은 짜여진 비선형성과 함께 일련의 선형 매핑을 수행합니다. (다층 신경망 제작하겠다.)
• 이 섹션에서는 데이터 전처리, 가중치 초기화 및 손실 함수와 관련된 추가 설계 선택 사항에 대해 설명합니다.

1.1 Data Preprocessing

There are three common forms of data preprocessing a data matrix X, where we will assume that X is of size [N x D] (N is the number of data, D is their dimensionality).

• 데이터 행렬 X를 전처리하는 세 가지 일반적인 데이터 형식이 있습니다. 여기서 X의 크기는 N x D라고 가정합니다.

Mean subtraction is the most common form of preprocessing.
It involves subtracting the mean across every individual feature in the data, and has the geometric interpretation of centering the cloud of data around the origin along every dimension.
In numpy, this operation would be implemented as: X -= np.mean(X, axis = 0).
With images specifically, for convenience it can be common to subtract a single value from all pixels (e.g. X -= np.mean(X)), or to do so separately across the three color channels.

• 평균 빼기는 전처리의 가장 일반적인 형태입니다.
• 여기에는 데이터의 모든 개별 기능에서 평균을 빼는 작업이 포함되며 모든 차원을 따라 원점을 중심으로 데이터를 중앙에 배치하는 기하학적 해석이 있습니다.
• numpy에서 이 연산은 X -= np.mean(X, axis = 0)으로 구현됩니다.

• 특히 이미지의 경우 편의상 모든 픽셀에서 단일 값을 빼거나(예: X -= np.mean(X)) 세 가지 색상 채널에서 별도로 수행하는 것이 일반적일 수 있습니다.

  정리 : 평균을 빼는것이 전처리에서 가장 일반적인 형태, 평균을 빼면 원점을 중심으로 데이터들이 중앙으로 배치됨, 단 이미지는 세 가지 생삭 처널에서 별도로 수행하는것이 일반적

Normalization refers to normalizing the data dimensions so that they are of approximately the same scale.
There are two common ways of achieving this normalization.
One is to divide each dimension by its standard deviation, once it has been zero-centered: (X /= np.std(X, axis = 0)).
Another form of this preprocessing normalizes each dimension so that the min and max along the dimension is -1 and 1 respectively.
It only makes sense to apply this preprocessing if you have a reason to believe that different input features have different scales (or units), but they should be of approximately equal importance to the learning algorithm.
In case of images, the relative scales of pixels are already approximately equal (and in range from 0 to 255), so it is not strictly necessary to perform this additional preprocessing step.

• 정규화는 데이터 차원을 정규화하여 거의 동일한 척도가 되도록 하는 것을 말합니다.
• 이 정규화를 달성하는 두 가지 일반적인 방법이 있습니다.
• 하나는 zero-centered 되면 각 차원을 표준 편차로 나누는 것입니다: (X /= np.std(X, axis = 0)).
• 다른 형태는 각 차원을 정규화하여 차원에 따른 최소값과 최대값이 각각 -1과 1이 되도록 합니다.
• 서로 다른 입력 기능이 서로 다른 척도(또는 단위)를 갖는다고 믿을 만한 이유가 있는 경우에만 이 전처리를 적용하는 것이 의미가 있지만 학습 알고리즘에 대해 거의 동일한 중요성을 가져야 합니다.

• 이미지의 경우, 픽셀의 상대 스케일은 이미 거의 동일(및 0에서 255 범위)하므로 이 추가 전처리 단계를 반드시 수행할 필요는 없습니다.

  정리 : 정규화는 동일한 척도를 스케일을 맞춘다. zero-centered 맞추고 normalized실행 하거나, 각 차원을 정규화하여 -1 ~ 1 사이값을 가지게 한다. 하지만 이미지는 0 ~ 255 스케일이 비슷하기에 zero-centered 하면 된다.

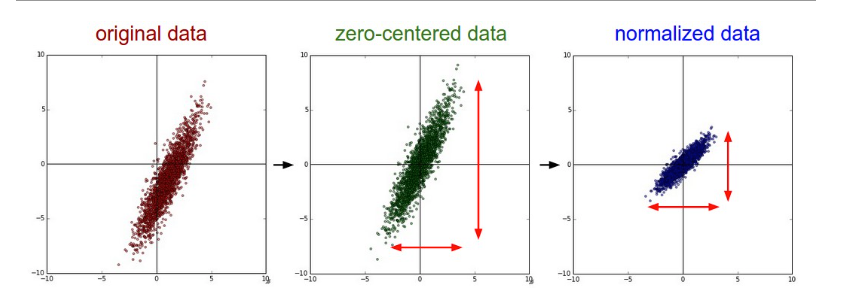
Common data preprocessing pipeline.
Left: Original toy, 2-dimensional input data.
Middle: The data is zero-centered by subtracting the mean in each dimension.The data cloud is now centered around the origin.
Right: Each dimension is additionally scaled by its standard deviation.
The red lines indicate the extent of the data - they are of unequal length in the middle, but of equal length on the right.

• 일반적인 데이터 전처리 파이프라인.
• 왼쪽: 원본, 2차원 입력 데이터.
• 중간: 데이터는 각 차원에서 평균을 빼서 0을 중심으로 합니다. 데이터는 이제 원본을 중심으로 합니다.
• 오른쪽: 각 차원은 표준 편차에 따라 추가로 조정됩니다.
• 빨간색 선은 데이터의 범위를 나타냅니다. 가운데는 길이가 같지 않지만 오른쪽은 길이가 같습니다.

PCA and Whitening is another form of preprocessing. In this process, the data is first centered as described above. Then, we can compute the covariance matrix that tells us about the correlation structure in the data:

• PCA 및 Whitening은 전처리의 또 다른 형태입니다. 이 과정에서 데이터는 위에서 설명한 것처럼 먼저 중앙에 배치됩니다. 그런 다음 데이터의 상관 구조에 대해 알려주는 공분산 행렬을 계산할 수 있습니다.

import numpy as np
# Assume input data matrix X of size [N x D]
X -= np.mean(X, axis=0)  # zero-center the data (important)
cov = np.dot(X.T, X) / X.shape[0]  # get the data covariance matrix

The (i,j) element of the data covariance matrix contains the covariance between i-th and j-th dimension of the data.
In particular, the diagonal of this matrix contains the variances.
Furthermore, the covariance matrix is symmetric and positive semi-definite. We can compute the SVD factorization of the data covariance matrix:

• 데이터 공분산 행렬의 (i,j) 요소는 데이터의 i번째 차원과 j번째 차원 사이의 공분산을 포함합니다.
• 특히 이 행렬의 대각선에는 분산이 포함됩니다.
• 또한 공분산 행렬은 대칭적이고 양의 positive semi-definite 입니다.데이터 공분산 행렬의 SVD 분해를 계산할 수 있습니다.

U,S,V = np.linalg.svd(cov)

where the columns of U are the eigenvectors and S is a 1-D array of the singular values.
To decorrelate the data, we project the original (but zero-centered) data into the eigenbasis:

• 여기서 U의 열은 고유 벡터이고 S는 특이값의 1차원 배열입니다.
• 데이터의 상관 관계를 해제하기 위해 원래(중심이 0인) 데이터를 고유 기저에 투영합니다.

Xrot = np.dot(X, U) # decorrelate the data

Notice that the columns of U are a set of orthonormal vectors (norm of 1, and orthogonal to each other), so they can be regarded as basis vectors.
The projection therefore corresponds to a rotation of the data in X so that the new axes are the eigenvectors.
If we were to compute the covariance matrix of Xrot, we would see that it is now diagonal.
A nice property of np.linalg.svd is that in its returned value U, the eigenvector columns are sorted by their eigenvalues.
We can use this to reduce the dimensionality of the data by only using the top few eigenvectors, and discarding the dimensions along which the data has no variance.
This is also sometimes referred to as Principal Component Analysis (PCA) dimensionality reduction:

• U의 열은 정규 직교 벡터(노름 1, 서로 직교) 집합이므로 기저 벡터로 간주할 수 있습니다.
• 따라서 투영은 새 축이 고유 벡터가 되도록 X의 데이터 회전에 해당합니다.
• Xrot의 공분산 행렬을 계산하면 이제 대각선임을 알 수 있습니다. np.linalg.svd의 좋은 속성은 반환된 값 U에서 고유 벡터 열이 고유 값으로 정렬된다는 것입니다.
• 이를 사용하여 상위 몇 개의 고유 벡터만 사용하고 데이터에 분산이 없는 차원을 버림으로써 데이터의 차원을 줄일 수 있습니다.
• 이를 PCA(Principal Component Analysis) 차원 축소라고도 합니다.

Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced becomes [N x 100]

After this operation, we would have reduced the original dataset of size [N x D] to one of size [N x 100], keeping the 100 dimensions of the data that contain the most variance.
It is very often the case that you can get very good performance by training linear classifiers or neural networks on the PCA-reduced datasets, obtaining savings in both space and time.

• 이 작업 후에 크기가 [N x D]인 원본 데이터 세트를 [N x 100] 크기 중 하나로 줄이고 가장 큰 분산을 포함하는 데이터의 100개 차원을 유지합니다.
• PCA 축소 데이터 세트에서 선형 분류기 또는 신경망을 훈련하여 공간과 시간을 모두 절약함으로써 매우 우수한 성능을 얻을 수 있는 경우가 매우 많습니다.

The last transformation you may see in practice is whitening. The whitening operation takes the data in the eigenbasis and divides every dimension by the eigenvalue to normalize the scale.
The geometric interpretation of this transformation is that if the input data is a multivariable gaussian, then the whitened data will be a gaussian with zero mean and identity covariance matrix.
This step would take the form:

• 실제로 볼 수 있는 마지막 변화는 whitening입니다.
• 화이트닝 작업은 고유 기저의 데이터를 가져와 모든 차원을 고유 값으로 나누어 스케일을 정규화합니다.
• 이 변환의 기하학적 해석은 입력 데이터가 다변수 가우시안인 경우 희게된 데이터는 평균이 0이고 항등 공분산 행렬이 있는 가우시안이 된다는 것입니다.
• 이 단계는 다음 형식을 취합니다.

# whiten the data:
# divide by the eigenvalues (which are square roots of the singular values)
Xwhite = Xrot / np.sqrt(S + 1e-5)

Warning: Exaggerating noise. Note that we’re adding 1e-5 (or a small constant) to prevent division by zero.
One weakness of this transformation is that it can greatly exaggerate the noise in the data, since it stretches all dimensions (including the irrelevant dimensions of tiny variance that are mostly noise) to be of equal size in the input.
This can in practice be mitigated by stronger smoothing (i.e. increasing 1e-5 to be a larger number).

• 경고: 과도한 noise. 0으로 나누는 것을 방지하기 위해 1e-5(또는 작은 상수)를 추가하고 있습니다.
• 이 변환의 한 가지 약점은 모든 차원(주로 잡음인 작은 분산의 관련 없는 차원 포함)을 입력에서 동일한 크기로 확장하기 때문에 데이터의 잡음을 크게 과장할 수 있다는 것입니다.
• 이는 실제로 더 강력한 평활화(즉, 1e-5를 더 큰 숫자로 증가)로 완화할 수 있습니다.

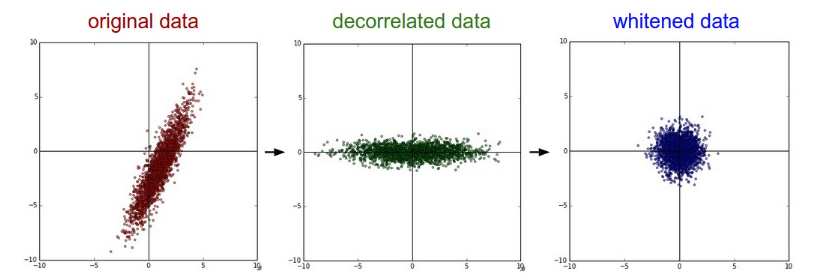
PCA / Whitening.
Left: Original toy, 2-dimensional input data. Middle: After performing PCA.
The data is centered at zero and then rotated into the eigenbasis of the data covariance matrix. This decorrelates the data (the covariance matrix becomes diagonal).
Right: Each dimension is additionally scaled by the eigenvalues, transforming the data covariance matrix into the identity matrix.
Geometrically, this corresponds to stretching and squeezing the data into an isotropic gaussian blob.

• 왼쪽: 원본 장난감, 2차원 입력 데이터. 중간: PCA 수행 후. 데이터는 0에 중심을 둔 다음 데이터 공분산 행렬의 고유 기준으로 회전합니다.
• 이렇게 하면 데이터의 상관 관계가 해제됩니다(공분산 행렬이 대각선이 됨).
• 오른쪽: 각 차원은 고유값에 의해 추가로 조정되어 데이터 공분산 행렬을 항등 행렬로 변환합니다.
• 기하학적으로 이는 데이터를 등방성 가우시안 블롭으로 늘리고 압축하는 것에 해당합니다.

We can also try to visualize these transformations with CIFAR-10 images.
The training set of CIFAR-10 is of size 50,000 x 3072, where every image is stretched out into a 3072-dimensional row vector.
We can then compute the [3072 x 3072] covariance matrix and compute its SVD decomposition (which can be relatively expensive).
What do the computed eigenvectors look like visually? An image might help:

• CIFAR-10 이미지로 이러한 변환을 시각화할 수도 있습니다.
• C- IFAR-10의 훈련 세트는 크기가 50,000 x 3072이며 모든 이미지가 3072차원 행 벡터로 확장됩니다.
• 그런 다음 [3072 x 3072] 공분산 행렬을 계산하고 SVD 분해(상대적으로 비쌀 수 있음)를 계산할 수 있습니다.
• 계산된 고유 벡터는 시각적으로 어떻게 보입니까? 이미지가 도움이 될 수 있습니다.

Left: An example set of 49 images. 2nd from Left: The top 144 out of 3072 eigenvectors. The top eigenvectors account for most of the variance in the data, and we can see that they correspond to lower frequencies in the images. 2nd from Right: The 49 images reduced with PCA, using the 144 eigenvectors shown here. That is, instead of expressing every image as a 3072-dimensional vector where each element is the brightness of a particular pixel at some location and channel, every image above is only represented with a 144-dimensional vector, where each element measures how much of each eigenvector adds up to make up the image. In order to visualize what image information has been retained in the 144 numbers, we must rotate back into the “pixel” basis of 3072 numbers. Since U is a rotation, this can be achieved by multiplying by U.transpose()[:144,:], and then visualizing the resulting 3072 numbers as the image. You can see that the images are slightly blurrier, reflecting the fact that the top eigenvectors capture lower frequencies. However, most of the information is still preserved. Right: Visualization of the “white” representation, where the variance along every one of the 144 dimensions is squashed to equal length. Here, the whitened 144 numbers are rotated back to image pixel basis by multiplying by U.transpose()[:144,:]. The lower frequencies (which accounted for most variance) are now negligible, while the higher frequencies (which account for relatively little variance originally) become exaggerated.

• 왼쪽: 49개 이미지의 예시 세트.
• 왼쪽에서 두 번째: 3072개의 고유 벡터 중 상위 144개.
• 상위 고유 벡터는 데이터의 분산 대부분을 설명하며 이미지의 낮은 주파수에 해당함을 알 수 있습니다.
• 오른쪽에서 두 번째: 여기에 표시된 144개의 고유 벡터를 사용하여 PCA로 축소된 49개의 이미지.
• 즉, 각 요소가 특정 위치 및 채널에서 특정 픽셀의 밝기인 3072차원 벡터로 모든 이미지를 표현하는 대신, 위의 모든 이미지는 144차원 벡터로만 표현되며 각 요소는 각 고유 벡터가 합쳐져 이미지를 구성합니다.
• 144개 숫자에 어떤 이미지 정보가 남아 있는지 시각화하려면 3072개 숫자의 “픽셀” 기준으로 다시 회전해야 합니다.
• U는 회전이므로 U.transpose()[:144,:]를 곱한 다음 결과 3072개의 숫자를 이미지로 시각화하면 됩니다.
• 상위 고유 벡터가 더 낮은 주파수를 캡처한다는 사실을 반영하여 이미지가 약간 더 흐릿함을 알 수 있습니다.
• 그러나 대부분의 정보는 여전히 보존됩니다.
• 오른쪽: 144차원의 모든 분산이 동일한 길이로 스쿼시되는 “흰색” 표현의 시각화.
• 여기서 하얗게 된 144개의 숫자는 U.transpose()[:144,:]를 곱하여 이미지 픽셀 기준으로 다시 회전됩니다.
• 더 낮은 주파수(대부분의 분산을 설명함)는 이제 무시할 수 있는 반면, 더 높은 주파수(원래 상대적으로 작은 분산을 설명함)는 과장됩니다.

In practice. We mention PCA/Whitening in these notes for completeness, but these transformations are not used with Convolutional Networks. However, it is very important to zero-center the data, and it is common to see normalization of every pixel as well.

• 실제로. 완전성을 위해 이 노트에서 PCA/Whitening 언급하지만 이러한 변환은 Convolutional Networks에서 사용되지 않습니다.
• 그러나 데이터를 제로 센터에 두는 것이 매우 중요하며 모든 픽셀의 정규화도 흔히 볼 수 있습니다.

Common pitfall. An important point to make about the preprocessing is that any preprocessing statistics (e.g. the data mean) must only be computed on the training data, and then applied to the validation / test data. E.g. computing the mean and subtracting it from every image across the entire dataset and then splitting the data into train/val/test splits would be a mistake. Instead, the mean must be computed only over the training data and then subtracted equally from all splits (train/val/test).

• 일반적인 함정. 전처리에 대해 알아야 할 중요한 점은 모든 전처리 통계(예: 데이터 평균)는 훈련 데이터에서만 계산된 다음 유효성 검사/테스트 데이터에 적용되어야 한다는 것입니다.
• 예를 들어 평균을 계산하고 전체 데이터 세트의 모든 이미지에서 이를 뺀 다음 데이터를 훈련/평가/테스트 분할로 분할하는 것은 실수입니다.
• 대신, 훈련 데이터에 대해서만 평균을 계산한 다음 모든 분할(훈련/평가/테스트)에서 동일하게 빼야 합니다.

1.2 Weight Initialization

We have seen how to construct a Neural Network architecture, and how to preprocess the data.
Before we can begin to train the network we have to initialize its parameters.

• 우리는 신경망 아키텍처를 구성하는 방법과 데이터를 전처리하는 방법을 살펴보았습니다.
• 네트워크 훈련을 시작하기 전에 매개변수를 초기화해야 합니다.

1.2.1 Pitfall: all zero initialization.

Lets start with what we should not do.
Note that we do not know what the final value of every weight should be in the trained network, but with proper data normalization it is reasonable to assume that approximately half of the weights will be positive and half of them will be negative. A reasonable-sounding idea then might be to set all the initial weights to zero, which we expect to be the “best guess” in expectation. This turns out to be a mistake, because if every neuron in the network computes the same output, then they will also all compute the same gradients during backpropagation and undergo the exact same parameter updates. In other words, there is no source of asymmetry between neurons if their weights are initialized to be the same.

• 함정: 모두 0으로 초기화. 하지 말아야 할 것부터 시작합시다.
• 훈련된 네트워크에서 모든 가중치의 최종 값이 무엇인지 알지 못하지만 적절한 데이터 정규화를 사용하면 가중치의 약 절반이 양수이고 절반이 음수라고 가정하는 것이 합리적입니다.
• 그럴듯하게 들리는 아이디어는 모든 초기 가중치를 0으로 설정하는 것일 수 있으며, 이는 우리가 기대하는 “최선의 추측”이 될 것으로 예상됩니다.
• 이것은 네트워크의 모든 뉴런이 동일한 출력을 계산하는 경우 역전파 중에 모두 동일한 기울기를 계산하고 정확히 동일한 매개변수 업데이트를 거치기 때문에 실수로 밝혀졌습니다.
• 즉, 가중치가 동일하게 초기화되면 뉴런 간에 비대칭의 원인이 없습니다.

1.2.2 Small random numbers.

Therefore, we still want the weights to be very close to zero, but as we have argued above, not identically zero.
As a solution, it is common to initialize the weights of the neurons to small numbers and refer to doing so as symmetry breaking.
The idea is that the neurons are all random and unique in the beginning, so they will compute distinct updates and integrate themselves as diverse parts of the full network.
The implementation for one weight matrix might look like W = 0.01* np.random.randn(D,H), where randn samples from a zero mean, unit standard deviation gaussian.
With this formulation, every neuron’s weight vector is initialized as a random vector sampled from a multi-dimensional gaussian, so the neurons point in random direction in the input space.
It is also possible to use small numbers drawn from a uniform distribution, but this seems to have relatively little impact on the final performance in practice.

• 작은 난수.
• 따라서 우리는 여전히 가중치가 0에 매우 가깝기를 원하지만 위에서 논의한 것처럼 동일하게 0은 아닙니다.
• 해결책으로 뉴런의 가중치를 작은 수로 초기화하는 것이 일반적이며 이를 대칭 깨짐이라고 합니다.
• 아이디어는 뉴런이 처음에는 모두 임의적이고 고유하므로 별개의 업데이트를 계산하고 전체 네트워크의 다양한 부분으로 통합된다는 것입니다.
• 하나의 가중치 행렬에 대한 구현은 W = 0.01* np.random.randn(D,H)와 같을 수 있습니다. 여기서 randn은 제로 평균, 단위 표준 편차 가우시안에서 샘플링합니다.
• 이 공식을 사용하면 모든 뉴런의 가중치 벡터가 다차원 가우시안에서 샘플링된 임의 벡터로 초기화되므로 뉴런은 입력 공간에서 임의의 방향을 가리킵니다.
• 균일 분포에서 가져온 작은 숫자를 사용하는 것도 가능하지만 실제로는 최종 성능에 상대적으로 거의 영향을 미치지 않는 것 같습니다.

Warning: It’s not necessarily the case that smaller numbers will work strictly better.
For example, a Neural Network layer that has very small weights will during backpropagation compute very small gradients on its data (since this gradient is proportional to the value of the weights).
This could greatly diminish the “gradient signal” flowing backward through a network, and could become a concern for deep networks.

• 경고: 반드시 작은 숫자가 더 잘 작동하는 것은 아닙니다.
• 예를 들어 가중치가 매우 작은 신경망 계층은 역전파 중에 데이터에 대한 매우 작은 그래디언트를 계산합니다(이 그래디언트는 가중치 값에 비례하기 때문).
• 이것은 네트워크를 통해 역류하는 “기울기 신호”를 크게 감소시킬 수 있으며 심층 네트워크에 대한 우려가 될 수 있습니다.

1.2.3 Calibrating the variances with 1/sqrt(n).

One problem with the above suggestion is that the distribution of the outputs from a randomly initialized neuron has a variance that grows with the number of inputs.
It turns out that we can normalize the variance of each neuron’s output to 1 by scaling its weight vector by the square root of its fan-in (i.e. its number of inputs).
That is, the recommended heuristic is to initialize each neuron’s weight vector as: w = np.random.randn(n) / sqrt(n), where n is the number of its inputs.
This ensures that all neurons in the network initially have approximately the same output distribution and empirically improves the rate of convergence.

• 1/sqrt(n)로 분산을 보정합니다.
• 위 제안의 한 가지 문제점은 임의로 초기화된 뉴런의 출력 분포가 입력 수에 따라 증가하는 분산을 갖는다는 것입니다.
• 가중치 벡터를 팬인(즉, 입력 수)의 제곱근으로 스케일링하여 각 뉴런 출력의 분산을 1로 정규화할 수 있음이 밝혀졌습니다.
• 즉, 권장되는 휴리스틱은 각 뉴런의 가중치 벡터를 w = np.random.randn(n) / sqrt(n)으로 초기화하는 것입니다. 여기서 n은 입력의 수입니다.
• 이렇게 하면 네트워크의 모든 뉴런이 초기에 거의 동일한 출력 분포를 가지며 경험적으로 수렴 속도가 향상됩니다.

The sketch of the derivation is as follows:
Consider the inner product $ (s = \sum_i^n w_i x_i) $ between the weights w and input x, which gives the raw activation of a neuron before the non-linearity.
We can examine the variance of s:

• 파생의 스케치는 다음과 같습니다.
• 가중치 w와 입력 x 사이의 내적 $ (s = \sum_i^n w_i x_i) $를 고려하십시오. 이는 비선형성 이전에 뉴런의 원시 활성화를 제공합니다.
• s의 분산을 조사할 수 있습니다.

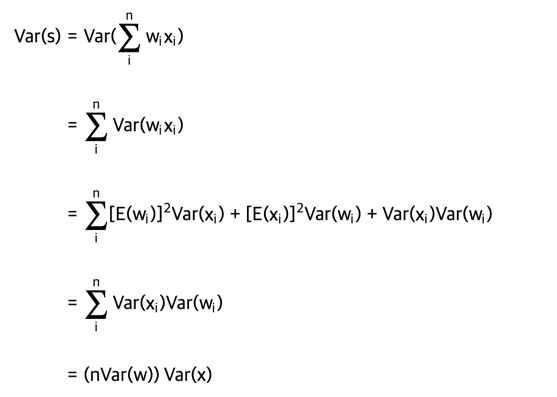
where in the first 2 steps we have used properties of variance. In third step we assumed zero mean inputs and weights, so E[xi]=E[wi]=0. Note that this is not generally the case: For example ReLU units will have a positive mean. In the last step we assumed that all wi,xi are identically distributed. From this derivation we can see that if we want s to have the same variance as all of its inputs x, then during initialization we should make sure that the variance of every weight wis 1/n.

• 여기서 처음 2단계에서는 분산 속성을 사용했습니다.
• 세 번째 단계에서 우리는 제로 평균 입력 및 가중치를 가정하므로 E[xi]=E[wi]=0입니다.
• 일반적으로 그렇지 않다는 점에 유의하십시오. 예를 들어 ReLU 단위는 양수 평균을 갖습니다.
• 마지막 단계에서 우리는 모든 wi,xi가 동일하게 분포되어 있다고 가정했습니다.
• 이 파생에서 우리는 s가 모든 입력 x와 동일한 분산을 갖기를 원한다면 초기화 중에 모든 가중치의 분산이 1/n이 되도록 해야 한다는 것을 알 수 있습니다.

And since $ (\text{Var}(aX) = a^2\text{Var}(X)) $ for a random variable X and a scalar a, this implies that we should draw from unit gaussian and then scale it by $ (a = \sqrt{1/n}) $, to make its variance $ (1/n) $. This gives the initialization w = np.random.randn(n) / sqrt(n).

• 그리고 랜덤 변수 X와 스칼라 a에 대해 $ (\text{Var}(aX) = a^2\text{Var}(X)) $ 이므로 단위 가우시안에서 그린 다음 $ (a = \sqrt{1/n}) $ 으로 크기를 조정해야 함을 의미합니다. 분산 $ (1/n) $.
• 이것은 초기화 w = np.random.randn(n) / sqrt(n)을 제공합니다.

A similar analysis is carried out in Understanding the difficulty of training deep feedforward neural networks by Glorot et al. In this paper, the authors end up recommending an initialization of the form $ ( \text{Var}(w) = 2/(n_{in} + n_{out}) ) $ where $ (n_{in}, n_{out}) $ are the number of units in the previous layer and the next layer. This is based on a compromise and an equivalent analysis of the backpropagated gradients. A more recent paper on this topic, Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification by He et al., derives an initialization specifically for ReLU neurons, reaching the conclusion that the variance of neurons in the network should be 2.0/n. T his gives the initialization w = np.random.randn(n) * sqrt(2.0/n), and is the current recommendation for use in practice in the specific case of neural networks with ReLU neurons.

• 유사한 분석이 Glorot et al의 심층 피드포워드 신경망 훈련의 어려움 이해에서 수행됩니다. 이 논문에서 저자는 결국 $ ( \text{Var}(w) = 2/(n_{in} + n_{out}) ) 형식의 초기화를 권장합니다.
• 여기서 $ (n_{in}, n_{out}) $ 은 이전 레이어와 다음 레이어의 단위 수입니다.
• 이는 역전파된 그래디언트의 절충 및 동등한 분석을 기반으로 합니다. 이 주제에 대한 더 최근의 논문인 Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification by He et al.은 특히 ReLU 뉴런에 대한 초기화를 유도하여 네트워크의 뉴런 분산이 2.0/이어야 한다는 결론에 도달했습니다. N. 이는 초기화 w = np.random.randn(n) * sqrt(2.0/n)을 제공하며 ReLU 뉴런이 있는 신경망의 특정 사례에서 실제로 사용하기 위한 현재 권장 사항입니다.

1.2.4 Sparse initialization.

Another way to address the uncalibrated variances problem is to set all weight matrices to zero, but to break symmetry every neuron is randomly connected (with weights sampled from a small gaussian as above) to a fixed number of neurons below it. A typical number of neurons to connect to may be as small as 10.

• 스파스 초기화. 보정되지 않은 분산 문제를 해결하는 또 다른 방법은 모든 가중치 행렬을 0으로 설정하는 것이지만 대칭을 깨기 위해 모든 뉴런이 그 아래의 고정된 수의 뉴런에 무작위로 연결됩니다(위와 같이 작은 가우시안에서 샘플링된 가중치 사용).
• 연결할 뉴런의 일반적인 수는 10개 정도로 작을 수 있습니다.

1.2.5 Initializing the biases.

It is possible and common to initialize the biases to be zero, since the asymmetry breaking is provided by the small random numbers in the weights. For ReLU non-linearities, some people like to use small constant value such as 0.01 for all biases because this ensures that all ReLU units fire in the beginning and therefore obtain and propagate some gradient. However, it is not clear if this provides a consistent improvement (in fact some results seem to indicate that this performs worse) and it is more common to simply use 0 bias initialization.

• 편향을 초기화합니다. 가중치의 작은 난수에 의해 비대칭 깨짐이 제공되기 때문에 편향을 0으로 초기화하는 것이 가능하고 일반적입니다.
• ReLU 비선형성의 경우 일부 사람들은 모든 편향에 대해 0.01과 같은 작은 상수 값을 사용하는 것을 좋아합니다. 이렇게 하면 모든 ReLU 장치가 처음에 실행되어 일부 기울기를 얻고 전파할 수 있기 때문입니다.
• 그러나 이것이 일관된 개선을 제공하는지 여부는 명확하지 않으며(실제로 일부 결과는 이것이 더 나쁜 성능을 나타내는 것으로 나타남) 단순히 0 바이어스 초기화를 사용하는 것이 더 일반적입니다.

In practice, the current recommendation is to use ReLU units and use the w = np.random.randn(n) * sqrt(2.0/n), as discussed in He et al..

• 실제로 현재 권장 사항은 He et al.에서 논의한 대로 ReLU 단위를 사용하고 w = np.random.randn(n) * sqrt(2.0/n)을 사용하는 것입니다.

1.3 Batch Normalization

A recently developed technique by Ioffe and Szegedy called Batch Normalization alleviates a lot of headaches with properly initializing neural networks by explicitly forcing the activations throughout a network to take on a unit gaussian distribution at the beginning of the training.
The core observation is that this is possible because normalization is a simple differentiable operation.
In the implementation, applying this technique usually amounts to insert the BatchNorm layer immediately after fully connected layers (or convolutional layers, as we’ll soon see), and before non-linearities.
We do not expand on this technique here because it is well described in the linked paper, but note that it has become a very common practice to use Batch Normalization in neural networks.
In practice networks that use Batch Normalization are significantly more robust to bad initialization.
Additionally, batch normalization can be interpreted as doing preprocessing at every layer of the network, but integrated into the network itself in a differentiable manner. Neat!

• Ioffe와 Szegedy가 최근에 개발한 Batch Normalization이라는 기술은 훈련 시작 시 네트워크 전체의 활성화가 단위 가우시안 분포를 취하도록 명시적으로 강제함으로써 신경망을 적절하게 초기화하여 많은 골칫거리를 완화합니다.
• 핵심 관찰은 정규화가 단순한 미분 가능 작업이기 때문에 이것이 가능하다는 것입니다.
• 구현에서 이 기술을 적용하면 일반적으로 완전히 연결된 레이어(또는 곧 보게 될 컨볼루션 레이어) 바로 뒤와 비선형성 앞에 BatchNorm 레이어를 삽입하는 것과 같습니다.
• 링크된 문서에 잘 설명되어 있기 때문에 여기서는 이 기술을 확장하지 않지만 신경망에서 배치 정규화를 사용하는 것은 매우 일반적인 관행이 되었습니다.
• 실제로 배치 정규화를 사용하는 네트워크는 잘못된 초기화에 훨씬 더 강력합니다.
• 또한 배치 정규화는 네트워크의 모든 계층에서 전처리를 수행하는 것으로 해석될 수 있지만 차별화 가능한 방식으로 네트워크 자체에 통합됩니다. 정돈된!

1.4 Regularization (L2/L1/Maxnorm/Dropout)

There are several ways of controlling the capacity of Neural Networks to prevent overfitting:

• 과적합을 방지하기 위해 신경망의 용량을 제어하는 방법에는 여러 가지가 있습니다.

L2 regularization is perhaps the most common form of regularization. It can be implemented by penalizing the squared magnitude of all parameters directly in the objective. That is, for every weight w in the network, we add the term $ (\frac{1}{2} \lambda w^2) $ to the objective, where λ is the regularization strength. It is common to see the factor of 12 in front because then the gradient of this term with respect to the parameter w is simply λw instead of 2λw. The L2 regularization has the intuitive interpretation of heavily penalizing peaky weight vectors and preferring diffuse weight vectors. As we discussed in the Linear Classification section, due to multiplicative interactions between weights and inputs this has the appealing property of encouraging the network to use all of its inputs a little rather than some of its inputs a lot. Lastly, notice that during gradient descent parameter update, using the L2 regularization ultimately means that every weight is decayed linearly: W += -lambda * W towards zero.

• L2 정규화는 아마도 정규화의 가장 일반적인 형태일 것입니다.
• 목표에서 직접 모든 매개변수의 제곱 크기에 페널티를 부여하여 구현할 수 있습니다.
• 즉, 네트워크의 모든 가중치 w에 대해 목표에 $ (\frac{1}{2} \lambda w^2) $라는 용어를 추가합니다. 여기서 λ는 정규화 강도입니다.
• 매개변수 w에 대한 이 항의 기울기가 단순히 2λw가 아니라 λw이기 때문에 앞에 12의 인수를 보는 것이 일반적입니다.
• L2 정규화는 정점 가중치 벡터에 크게 패널티를 부여하고 확산 가중치 벡터를 선호한다는 직관적인 해석을 제공합니다.
• 선형 분류 섹션에서 논의한 것처럼 가중치와 입력 간의 곱셈 상호 작용으로 인해 네트워크가 일부 입력을 많이 사용하기보다는 모든 입력을 조금씩 사용하도록 권장하는 매력적인 속성이 있습니다.
• 마지막으로, 경사하강법 매개변수 업데이트 중에 L2 정규화를 사용하면 궁극적으로 모든 가중치가 선형으로 감소한다는 것을 의미합니다. W += -lambda * W는 0을 향합니다.

L1 regularization is another relatively common form of regularization, where for each weight w we add the term λ∣w∣ to the objective. It is possible to combine the L1 regularization with the L2 regularization: λ1∣w∣+λ2w2 (this is called Elastic net regularization). The L1 regularization has the intriguing property that it leads the weight vectors to become sparse during optimization (i.e. very close to exactly zero). In other words, neurons with L1 regularization end up using only a sparse subset of their most important inputs and become nearly invariant to the “noisy” inputs. In comparison, final weight vectors from L2 regularization are usually diffuse, small numbers. In practice, if you are not concerned with explicit feature selection, L2 regularization can be expected to give superior performance over L1.

• L1 정규화는 상대적으로 일반적인 정규화의 또 다른 형태로 각 가중치 w에 대해 용어 λ∣w∣를 목적에 추가합니다.
• L1 정규화를 L2 정규화와 결합하는 것이 가능합니다: λ1∣w∣+λ2w2(탄력적 순 정규화라고 함).
• L1 정규화에는 최적화 중에 가중치 벡터가 희박해지게(즉, 정확히 0에 매우 가깝게) 만드는 흥미로운 속성이 있습니다.
• 즉, L1 정규화를 사용하는 뉴런은 가장 중요한 입력의 희소한 하위 집합만 사용하게 되고 “잡음이 많은” 입력에 대해 거의 변하지 않게 됩니다.
• 이에 비해 L2 정규화의 최종 가중치 벡터는 일반적으로 확산되고 작은 숫자입니다.
• 실제로 명시적인 기능 선택에 관심이 없는 경우 L2 정규화가 L1보다 우수한 성능을 제공할 것으로 예상할 수 있습니다.

Max norm constraints. Another form of regularization is to enforce an absolute upper bound on the magnitude of the weight vector for every neuron and use projected gradient descent to enforce the constraint. In practice, this corresponds to performing the parameter update as normal, and then enforcing the constraint by clamping the weight vector w-> of every neuron to satisfy ‖w-> ‖2<c. Typical values of c are on orders of 3 or 4. Some people report improvements when using this form of regularization. One of its appealing properties is that network cannot “explode” even when the learning rates are set too high because the updates are always bounded.

• 최대 규범 제약.
• 정규화의 또 다른 형태는 모든 뉴런에 대해 가중치 벡터의 크기에 절대 상한을 적용하고 투영된 경사 하강법을 사용하여 제약 조건을 적용하는 것입니다.
• 실제로 이것은 매개변수 업데이트를 정상적으로 수행한 다음 ‖w-> ‖2를 고정하여 제약 조건을 적용하는 것에 해당합니다.
• c의 일반적인 값은 3차 또는 4차입니다. 어떤 사람들은 이 형식의 정규화를 사용할 때 개선되었다고 보고합니다.
• 매력적인 속성 중 하나는 업데이트가 항상 제한되어 있기 때문에 학습률이 너무 높게 설정되어 있어도 네트워크가 “폭발”할 수 없다는 것입니다.

Dropout is an extremely effective, simple and recently introduced regularization technique by Srivastava et al. in Dropout: A Simple Way to Prevent Neural Networks from Overfitting (pdf) that complements the other methods (L1, L2, maxnorm). While training, dropout is implemented by only keeping a neuron active with some probability p (a hyperparameter), or setting it to zero otherwise.

• 드롭아웃은 Srivastava 등이 최근 도입한 매우 효과적이고 간단한 정규화 기법입니다.
• in Dropout: A Simple Way to Prevent Neural Networks from Overfitting (pdf) 다른 방법(L1, L2, maxnorm)을 보완합니다.
• 훈련하는 동안, 일부 확률 p(초매개변수)로 뉴런을 활성 상태로 유지하거나 그렇지 않으면 0으로 설정하여 드롭아웃을 구현합니다.

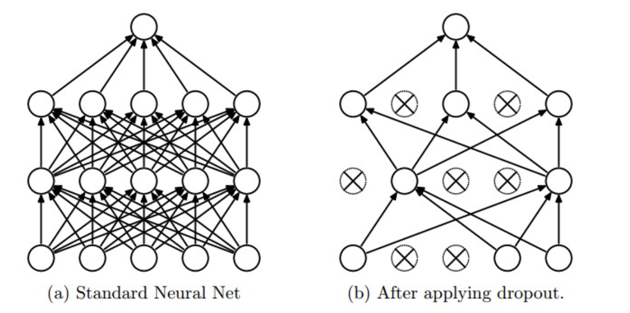
Figure taken from the Dropout paper that illustrates the idea. During training, Dropout can be interpreted as sampling a Neural Network within the full Neural Network, and only updating the parameters of the sampled network based on the input data. (However, the exponential number of possible sampled networks are not independent because they share the parameters.) During testing there is no dropout applied, with the interpretation of evaluating an averaged prediction across the exponentially-sized ensemble of all sub-networks (more about ensembles in the next section).

• 아이디어를 설명하는 드롭아웃 용지에서 가져온 그림입니다.
• 교육 중에 드롭아웃은 전체 신경망 내에서 신경망을 샘플링하고 입력 데이터를 기반으로 샘플링된 신경망의 매개변수만 업데이트하는 것으로 해석할 수 있습니다.
• (그러나 가능한 샘플링된 네트워크의 기하급수적 수는 매개변수를 공유하기 때문에 독립적이지 않습니다.)
• 테스트 중에는 모든 하위 네트워크의 기하급수적으로 크기가 지정된 앙상블에서 평균 예측을 평가하는 해석과 함께 드롭아웃이 적용되지 않습니다(자세한 내용은 다음 섹션의 앙상블).

Vanilla dropout in an example 3-layer Neural Network would be implemented as follows:

• 예제 3계층 신경망에서 바닐라 드롭아웃은 다음과 같이 구현됩니다.

""" Vanilla Dropout: Not recommended implementation (see notes below) """

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  """ X contains the data """

  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = np.random.rand(*H1.shape) < p  # first dropout mask
  H1 *= U1  # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = np.random.rand(*H2.shape) < p  # second dropout mask
  H2 *= U2  # drop!
  out = np.dot(W3, H2) + b3

  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)


def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) * p  # NOTE: scale the activations
  H2 = np.maximum(0, np.dot(W2, H1) + b2) * p  # NOTE: scale the activations
  out = np.dot(W3, H2) + b3

In the code above, inside the train_step function we have performed dropout twice: on the first hidden layer and on the second hidden layer. It is also possible to perform dropout right on the input layer, in which case we would also create a binary mask for the input X. The backward pass remains unchanged, but of course has to take into account the generated masks U1,U2.

• 위의 코드에서 train_step 함수 내에서 첫 번째 숨겨진 레이어와 두 번째 숨겨진 레이어에서 드롭아웃을 두 번 수행했습니다.
• 입력 레이어에서 바로 드롭아웃을 수행하는 것도 가능합니다. 이 경우 입력 X에 대한 바이너리 마스크도 생성합니다.
• 역방향 패스는 변경되지 않지만 물론 생성된 마스크 U1, U2를 고려해야 합니다.

Crucially, note that in the predict function we are not dropping anymore, but we are performing a scaling of both hidden layer outputs by p. This is important because at test time all neurons see all their inputs, so we want the outputs of neurons at test time to be identical to their expected outputs at training time. For example, in case of p=0.5, the neurons must halve their outputs at test time to have the same output as they had during training time (in expectation). To see this, consider an output of a neuron x (before dropout). With dropout, the expected output from this neuron will become px+(1−p)0, because the neuron’s output will be set to zero with probability 1−p. At test time, when we keep the neuron always active, we must adjust x→px to keep the same expected output. It can also be shown that performing this attenuation at test time can be related to the process of iterating over all the possible binary masks (and therefore all the exponentially many sub-networks) and computing their ensemble prediction.

• 결정적으로, 예측 함수에서 우리는 더 이상 드롭하지 않지만 숨겨진 레이어 출력 모두를 p로 스케일링합니다.
• 이는 테스트 시간에 모든 뉴런이 모든 입력을 보기 때문에 중요하므로 테스트 시간의 뉴런 출력이 훈련 시간의 예상 출력과 동일하기를 원합니다.
• 예를 들어, p=0.5인 경우 뉴런은 테스트 시간에 출력을 절반으로 줄여 훈련 시간 동안(예상) 동일한 출력을 가져야 합니다.
• 이를 확인하려면 뉴런 x(드롭아웃 전)의 출력을 고려하십시오. 드롭아웃을 사용하면 뉴런의 출력이 확률 1-p로 0으로 설정되기 때문에 이 뉴런의 예상 출력은 px+(1-p)0이 됩니다.
• 테스트 시간에 뉴런을 항상 활성 상태로 유지하려면 동일한 예상 출력을 유지하기 위해 x→px를 조정해야 합니다.
• 또한 테스트 시간에 이 감쇠를 수행하는 것은 가능한 모든 이진 마스크(따라서 모든 기하급수적으로 많은 하위 네트워크)를 반복하고 앙상블 예측을 계산하는 프로세스와 관련될 수 있음을 보여줄 수 있습니다.

The undesirable property of the scheme presented above is that we must scale the activations by p at test time. Since test-time performance is so critical, it is always preferable to use inverted dropout, which performs the scaling at train time, leaving the forward pass at test time untouched. Additionally, this has the appealing property that the prediction code can remain untouched when you decide to tweak where you apply dropout, or if at all. Inverted dropout looks as follows:

• 위에 제시된 계획의 바람직하지 않은 속성은 테스트 시간에 p만큼 활성화를 스케일링해야 한다는 것입니다.
• 테스트 시간 성능이 매우 중요하기 때문에 훈련 시간에 스케일링을 수행하고 테스트 시간의 포워드 패스는 그대로 두는 반전된 드롭아웃을 사용하는 것이 항상 바람직합니다.
• 또한 여기에는 드롭아웃을 적용하는 위치를 조정하기로 결정하거나 적용하는 경우 예측 코드가 그대로 유지될 수 있다는 매력적인 속성이 있습니다. 반전 드롭아웃은 다음과 같습니다.

#Inverted Dropout: Recommended implementation example.
#We drop and scale at train time and don't do anything at test time.
"""

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = (np.random.rand(*H1.shape) < p) / p # first dropout mask. Notice /p!
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask. Notice /p!
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3
  
  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)
  
def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  out = np.dot(W3, H2) + b3

There has a been a large amount of research after the first introduction of dropout that tries to understand the source of its power in practice, and its relation to the other regularization techniques. Recommended further reading for an interested reader includes:

• 드롭아웃이 처음 도입된 후 실제로 그 힘의 근원을 이해하고 다른 정규화 기술과의 관계를 이해하려는 많은 연구가 있었습니다.
• 관심 있는 독자에게 권장되는 추가 자료는 다음과 같습니다.

Dropout paper by Srivastava et al. 2014. Dropout Training as Adaptive Regularization: “we show that the dropout regularizer is first-order equivalent to an L2 regularizer applied after scaling the features by an estimate of the inverse diagonal Fisher information matrix”.

• Srivastava et al.의 드롭아웃 페이퍼. 2014.
• 적응형 정규화로서의 드롭아웃 훈련: “우리는 드롭아웃 정규화가 역대각 피셔 정보 행렬의 추정으로 기능을 스케일링한 후 적용된 L2 정규화와 1차적으로 동일함을 보여줍니다.”

Theme of noise in forward pass. Dropout falls into a more general category of methods that introduce stochastic behavior in the forward pass of the network. During testing, the noise is marginalized over analytically (as is the case with dropout when multiplying by p), or numerically (e.g. via sampling, by performing several forward passes with different random decisions and then averaging over them). An example of other research in this direction includes DropConnect, where a random set of weights is instead set to zero during forward pass. As foreshadowing, Convolutional Neural Networks also take advantage of this theme with methods such as stochastic pooling, fractional pooling, and data augmentation. We will go into details of these methods later.

• 포워드 패스의 노이즈 테마.
• 드롭아웃은 네트워크의 순방향 전달에서 확률적 동작을 도입하는 보다 일반적인 방법 범주에 속합니다.
• 테스트 중에 노이즈는 분석적으로(p를 곱할 때 드롭아웃의 경우와 같이) 또는 수치적으로(예: 샘플링을 통해, 서로 다른 무작위 결정으로 여러 순방향 패스를 수행한 다음 평균을 내어) 주변화됩니다.
• 이 방향에 대한 다른 연구의 예로는 정방향 통과 중에 임의의 가중치 집합이 0으로 설정되는 DropConnect가 있습니다.
• 복선으로 Convolutional Neural Networks는 확률적 풀링, 분수 풀링 및 데이터 확대와 같은 방법으로 이 주제를 활용합니다. 나중에 이러한 방법에 대해 자세히 설명하겠습니다.

Bias regularization. As we already mentioned in the Linear Classification section, it is not common to regularize the bias parameters because they do not interact with the data through multiplicative interactions, and therefore do not have the interpretation of controlling the influence of a data dimension on the final objective. However, in practical applications (and with proper data preprocessing) regularizing the bias rarely leads to significantly worse performance. This is likely because there are very few bias terms compared to all the weights, so the classifier can “afford to” use the biases if it needs them to obtain a better data loss.

• 바이어스 정규화.
• 선형 분류 섹션에서 이미 언급했듯이 편향 매개변수는 곱셈 상호작용을 통해 데이터와 상호작용하지 않으므로 최종 목적에 대한 데이터 차원의 영향을 제어하는 해석이 없기 때문에 편향 매개변수를 정규화하는 것은 일반적이지 않습니다. .
• 그러나 실제 응용 프로그램(및 적절한 데이터 사전 처리)에서 편향을 정규화해도 성능이 크게 저하되는 경우는 거의 없습니다.
• 이는 모든 가중치에 비해 편향 항이 거의 없기 때문에 분류기가 더 나은 데이터 손실을 얻기 위해 편향이 필요한 경우 편향을 “사용”할 수 있기 때문일 수 있습니다.

Per-layer regularization. It is not very common to regularize different layers to different amounts (except perhaps the output layer). Relatively few results regarding this idea have been published in the literature.

레이어별 정규화.

• 다른 레이어를 다른 양으로 정규화하는 것은 그리 일반적이지 않습니다(아마도 출력 레이어 제외).
• 이 아이디어에 관한 비교적 적은 결과가 문헌에 발표되었습니다.

In practice: It is most common to use a single, global L2 regularization strength that is cross-validated. It is also common to combine this with dropout applied after all layers. The value of p=0.5 is a reasonable default, but this can be tuned on validation data.

• 실제로: 교차 검증된 단일 전역 L2 정규화 강도를 사용하는 것이 가장 일반적입니다.
• 이것을 모든 레이어 후에 적용되는 드롭아웃과 결합하는 것도 일반적입니다.
• p=0.5 값은 합리적인 기본값이지만 검증 데이터에서 조정할 수 있습니다.

3. Loss functions

We have discussed the regularization loss part of the objective, which can be seen as penalizing some measure of complexity of the model.
The second part of an objective is the data loss, which in a supervised learning problem measures the compatibility between a prediction (e.g. the class scores in classification) and the ground truth label.
The data loss takes the form of an average over the data losses for every individual example.
That is,$ (L = \frac{1}{N} \sum_i L_i) where (N) $ is the number of training data.
Lets abbreviate $ (f = f(x_i; W)) $ to be the activations of the output layer in a Neural Network.
There are several types of problems you might want to solve in practice:

• 우리는 목표의 정규화 손실 부분에 대해 논의했으며, 이는 모델의 복잡성 측정에 불이익을 주는 것으로 볼 수 있습니다.
• 목표의 두 번째 부분은 감독 학습 문제에서 예측(예: 분류의 클래스 점수)과 ground truth 레이블 간의 호환성을 측정하는 데이터 손실입니다.
• 데이터 손실은 모든 개별 예에 대한 데이터 손실에 대한 평균의 형태를 취합니다.
• 즉, $ (L = \frac{1}{N} \sum_i L_i) $ 요기서 N은 학습 데이터의 개수입니다.
• 신경망에서 출력 레이어의 활성화를 $ (f = f(x_i; W)) $로 축약합니다.
• 실제로 해결하고자 하는 몇 가지 유형의 문제가 있습니다.

Classification is the case that we have so far discussed at length. Here, we assume a dataset of examples and a single correct label (out of a fixed set) for each example. One of two most commonly seen cost functions in this setting is the SVM (e.g. the Weston Watkins formulation):

• 분류는 우리가 지금까지 길게 논의한 경우입니다.
• 여기서는 예제의 데이터 세트와 각 예제에 대해 하나의 올바른 레이블(고정된 세트 외)을 가정합니다.
• 이 설정에서 가장 흔히 볼 수 있는 두 가지 비용 함수 중 하나는 SVM(예: Weston Watkins 공식)입니다.

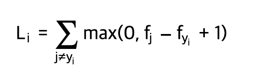
As we briefly alluded to, some people report better performance with the squared hinge loss (i.e. instead using $ (\max(0, f_j - f_{y_i} + 1)^2)) $.
The second common choice is the Softmax classifier that uses the cross-entropy loss:

• 우리가 간략하게 언급했듯이 일부 사람들은 제곱 힌지 손실로 더 나은 성능을 보고합니다(즉, 대신 $ (\max(0, f_j - f_{y_i} + 1)^2)) $ 사용).
• 두 번째 일반적인 선택은 교차 엔트로피 손실을 사용하는 Softmax 분류기입니다.

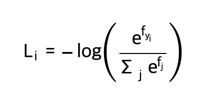
Problem: Large number of classes. When the set of labels is very large (e.g. words in English dictionary, or ImageNet which contains 22,000 categories), computing the full softmax probabilities becomes expensive. For certain applications, approximate versions are popular. For instance, it may be helpful to use Hierarchical Softmax in natural language processing tasks (see one explanation here (pdf)). The hierarchical softmax decomposes words as labels in a tree. Each label is then represented as a path along the tree, and a Softmax classifier is trained at every node of the tree to disambiguate between the left and right branch. The structure of the tree strongly impacts the performance and is generally problem-dependent.

• 문제: 많은 수의 클래스.
• 레이블 집합이 매우 큰 경우(예: 영어 사전의 단어 또는 22,000개의 범주를 포함하는 ImageNet) 전체 소프트맥스 확률을 계산하는 데 비용이 많이 듭니다.
• 특정 응용 프로그램의 경우 대략적인 버전이 널리 사용됩니다.
• 예를 들어, 자연어 처리 작업에서 Hierarchical Softmax를 사용하는 것이 도움이 될 수 있습니다(여기에서 한 가지 설명 참조(pdf)).
• 계층적 소프트맥스는 단어를 트리의 레이블로 분해합니다.
• 그런 다음 각 레이블은 트리를 따라 경로로 표시되고 Softmax 분류기는 트리의 모든 노드에서 훈련되어 왼쪽 및 오른쪽 분기 사이를 구분합니다.
• 트리의 구조는 성능에 큰 영향을 미치며 일반적으로 문제에 따라 다릅니다.

Attribute classification. Both losses above assume that there is a single correct answer yi. But what if yi is a binary vector where every example may or may not have a certain attribute, and where the attributes are not exclusive? For example, images on Instagram can be thought of as labeled with a certain subset of hashtags from a large set of all hashtags, and an image may contain multiple. A sensible approach in this case is to build a binary classifier for every single attribute independently. For example, a binary classifier for each category independently would take the form:

• 속성 분류.
• 위의 두 손실 모두 하나의 정답 yi가 있다고 가정합니다.
• 그러나 yi가 모든 예가 특정 속성을 가질 수도 있고 갖지 않을 수도 있고 속성이 배타적이지 않은 이진 벡터라면 어떻게 될까요?
• 예를 들어 Instagram의 이미지는 모든 해시태그의 큰 집합에서 특정 해시태그 하위 집합으로 레이블이 지정된 것으로 생각할 수 있으며 이미지에는 여러 해시태그가 포함될 수 있습니다.
• 이 경우 합리적인 접근 방식은 모든 단일 속성에 대한 이진 분류기를 독립적으로 구축하는 것입니다.
• 예를 들어 각 범주에 대한 이진 분류기는 독립적으로 다음과 같은 형식을 취합니다.

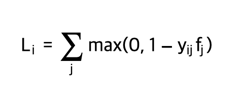
where the sum is over all categories j, and yij is either +1 or -1 depending on whether the i-th example is labeled with the j-th attribute, and the score vector fj will be positive when the class is predicted to be present and negative otherwise. Notice that loss is accumulated if a positive example has score less than +1, or when a negative example has score greater than -1.

• 여기서 합은 모든 범주 j에 걸쳐 있고, yj는 i번째 예제가 j번째 속성으로 레이블링되었는지 여부에 따라 +1 또는 -1이며, 클래스가 존재할 것으로 예측될 때 점수 벡터 fj는 양수이고 그렇지 않으면 음수입니다.
• 긍정적인 예의 점수가 +1 미만이거나 부정적인 예의 점수가 -1보다 큰 경우 손실이 누적됩니다.

An alternative to this loss would be to train a logistic regression classifier for every attribute independently. A binary logistic regression classifier has only two classes (0,1), and calculates the probability of class 1 as:

• 이 손실에 대한 대안은 모든 속성에 대해 독립적으로 로지스틱 회귀 분류기를 훈련하는 것입니다.
• 이진 로지스틱 회귀 분류기에는 두 개의 클래스(0,1)만 있으며 클래스 1의 확률을 다음과 같이 계산합니다.

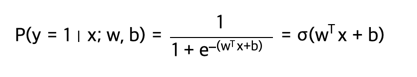
Since the probabilities of class 1 and 0 sum to one, the probability for class 0 is $ (P(y = 0 \mid x; w, b) = 1 - P(y = 1 \mid x; w,b)) $. Hence, an example is classified as a positive example (y = 1) if $ (\sigma (w^Tx + b) > 0.5) $, or equivalently if the score $ (w^Tx +b > 0) $. The loss function then maximizes this probability. You can convince yourself that this simplifies to minimizing the negative log-likelihood:

• 클래스 1과 0의 확률의 합은 1이므로 클래스 0의 확률은 $ (P(y = 0 \mid x; w, b) = 1 - P(y = 1 \mid x; w,b)) $입니다.
• 따라서 예는 $ (\sigma (w^Tx + b) > 0.5) $ 인 경우 또는 점수 $ (w^Tx +b > 0) $ 인 경우 포지티브 예(y = 1)로 분류됩니다.
• 그런 다음 손실 함수는 이 확률을 최대화합니다.
• 이것이 음의 로그 우도를 최소화하는 것으로 단순화된다는 것을 스스로 확신할 수 있습니다.

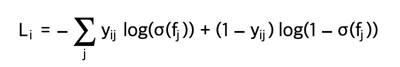
where the labels $ (y_{ij})$ are assumed to be either 1 (positive) or 0 (negative), and σ(⋅) is the sigmoid function. The expression above can look scary but the gradient on f is in fact extremely simple and intuitive: $ (\partial{L_i} / \partial{f_j} = \sigma(f_j) - y_{ij}) $ (as you can double check yourself by taking the derivatives).

• 여기서 레이블 $ (y_{ij})$ 는 1(양수) 또는 0(음수)으로 가정하고 σ(⋅)는 시그모이드 함수입니다.
• 위의 식은 무섭게 보일 수 있지만 f의 그래디언트는 사실 매우 간단하고 직관적입니다. $ (\partial{L_i} / \partial{f_j} = \sigma(f_j) - y_{ij}) $

Regression is the task of predicting real-valued quantities, such as the price of houses or the length of something in an image. For this task, it is common to compute the loss between the predicted quantity and the true answer and then measure the L2 squared norm, or L1 norm of the difference. The L2 norm squared would compute the loss for a single example of the form:

• 회귀는 주택 가격이나 이미지의 길이와 같은 실제 가치 수량을 예측하는 작업입니다.
• 이 작업의 경우 예측된 수량과 참 답 사이의 손실을 계산한 다음 차이의 L2 제곱 노름 또는 L1 노름을 측정하는 것이 일반적입니다.
• L2 표준 제곱은 다음 형식의 단일 예에 대한 손실을 계산합니다.

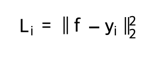
where the sum ∑j is a sum over all dimensions of the desired prediction, if there is more than one quantity being predicted. Looking at only the j-th dimension of the i-th example and denoting the difference between the true and the predicted value by δij, the gradient for this dimension (i.e. ∂Li/∂fj) is easily derived to be either δij with the L2 norm, or sign(δij). That is, the gradient on the score will either be directly proportional to the difference in the error, or it will be fixed and only inherit the sign of the difference.

• 여기서 합계 ∑j는 예측되는 양이 둘 이상인 경우 원하는 예측의 모든 차원에 대한 합계입니다.
• i번째 예제의 j번째 차원만 보고 참 값과 예측 값의 차이를 δij로 표시하면, 이 차원에 대한 기울기(즉, ∂Li/∂fj)는 L2 표준을 가진 δij 또는 부호(δij)로 쉽게 유도됩니다.
• 즉, 점수의 변화도는 오류의 차이에 정비례하거나 고정되어 차이의 부호만 상속합니다.

Word of caution: It is important to note that the L2 loss is much harder to optimize than a more stable loss such as Softmax. Intuitively, it requires a very fragile and specific property from the network to output exactly one correct value for each input (and its augmentations). Notice that this is not the case with Softmax, where the precise value of each score is less important: It only matters that their magnitudes are appropriate. Additionally, the L2 loss is less robust because outliers can introduce huge gradients. When faced with a regression problem, first consider if it is absolutely inadequate to quantize the output into bins. For example, if you are predicting star rating for a product, it might work much better to use 5 independent classifiers for ratings of 1-5 stars instead of a regression loss. Classification has the additional benefit that it can give you a distribution over the regression outputs, not just a single output with no indication of its confidence. If you’re certain that classification is not appropriate, use the L2 but be careful: For example, the L2 is more fragile and applying dropout in the network (especially in the layer right before the L2 loss) is not a great idea.

• 주의 사항: L2 손실은 Softmax와 같은 안정적인 손실보다 최적화하기가 훨씬 더 어렵다는 점에 유의해야 합니다.
• 직관적으로 각 입력(및 그 증가)에 대해 정확히 하나의 올바른 값을 출력하려면 네트워크에서 매우 취약하고 특정한 속성이 필요합니다.
• 이것은 각 점수의 정확한 값이 덜 중요한 Softmax의 경우가 아니라는 점에 유의하십시오. 점수의 크기가 적절한지 여부만 중요합니다.
• 또한 L2 손실은 이상값이 큰 기울기를 도입할 수 있기 때문에 덜 강력합니다.
• 회귀 문제에 직면했을 때 먼저 출력을 빈으로 양자화하는 것이 절대적으로 부적합한지 고려하십시오.
• 예를 들어 제품에 대한 별점을 예측하는 경우 회귀 손실 대신 별 1~5개 등급에 대해 5개의 독립적인 분류기를 사용하는 것이 훨씬 더 효과적일 수 있습니다.
• 분류는 신뢰도 표시가 없는 단일 출력이 아니라 회귀 출력에 대한 분포를 제공할 수 있다는 추가적인 이점이 있습니다.
• 분류가 적절하지 않다고 확신하는 경우 L2를 사용하되 주의하십시오. 예를 들어 L2는 더 취약하고 네트워크(특히 L2 손실 직전 계층)에서 드롭아웃을 적용하는 것은 좋은 생각이 아닙니다.

When faced with a regression task, first consider if it is absolutely necessary. Instead, have a strong preference to discretizing your outputs to bins and perform classification over them whenever possible.

• 회귀 작업에 직면하면 먼저 그것이 절대적으로 필요한지 고려하십시오.
• 대신 출력을 빈으로 이산화하고 가능할 때마다 분류를 수행하는 것을 선호합니다.

Structured prediction. The structured loss refers to a case where the labels can be arbitrary structures such as graphs, trees, or other complex objects. Usually it is also assumed that the space of structures is very large and not easily enumerable. The basic idea behind the structured SVM loss is to demand a margin between the correct structure yi and the highest-scoring incorrect structure. It is not common to solve this problem as a simple unconstrained optimization problem with gradient descent. Instead, special solvers are usually devised so that the specific simplifying assumptions of the structure space can be taken advantage of. We mention the problem briefly but consider the specifics to be outside of the scope of the class.

• 구조화된 예측.
• 구조적 손실은 레이블이 그래프, 트리 또는 기타 복잡한 개체와 같은 임의의 구조일 수 있는 경우를 말합니다.
• 일반적으로 구조의 공간은 매우 크고 쉽게 열거할 수 없다고 가정합니다.
• 구조화된 SVM 손실의 기본 아이디어는 올바른 구조 yi와 최고 점수의 잘못된 구조 사이에 마진을 요구하는 것입니다.
• 이 문제를 경사 하강법을 사용하여 단순한 제약 없는 최적화 문제로 해결하는 것은 일반적이지 않습니다.
• 대신 구조 공간의 특정 단순화 가정을 활용할 수 있도록 일반적으로 특수 솔버가 고안됩니다.
• 우리는 문제를 간략하게 언급하지만 세부 사항은 수업 범위를 벗어나는 것으로 간주합니다.

4. Summary

5. Additional references

• https://cs231n.github.io