과제1. Implement a Softmax classifier
cs231n 과제1. Implement a Softmax classifier 정리
1.1 소개
알고리즘을 사용하면서 대표적인 분류 문제를 해결하기 위헤 사용하는 Loss Function Multiclass SVM loss, sotfmax classifier 두가지로 분류가 된다. 이번시간에는 SVM 사용 방법에 대한 설명이다.
앞에서는 SVM 사용한 다중 분류를 사용했다면, 이번시간에는 딥러닝에서 많이 사용하는 분류 방법인 sotfmax classifier 구현할 것이다. sotfmax classifier 대표적인 장점은 확률 값으로 score 점수를 나타내기 때문에 쉽게 해석이 가능하다.
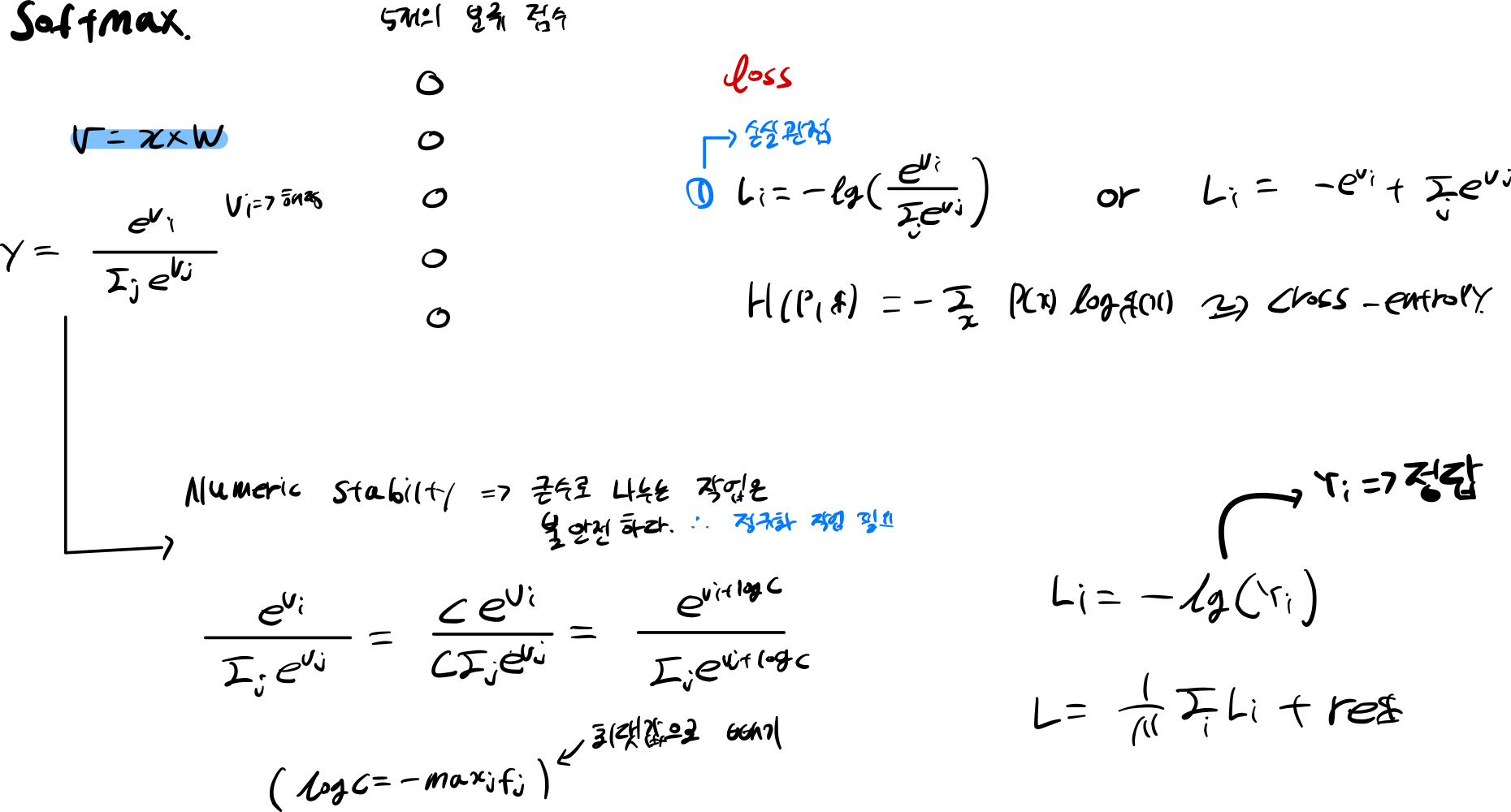
\[y_i = (\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} })\]그림은 softmax 함수이다. 모든 클래스 점수를 exp 시켜 모두 더하고 해당 클래스 점수를 분자로 표기해 해당 클래스의 확률을 구하게된다.
Softmax 총합은 1로 고정한다.
softmax 손실 함수는 \(-\log(y_i)\) 사용해 해당 클래스의 손실도를 구하게 된다.
\[P(y_i \mid x_i; W) = \frac{e^{f_{y_i}}}{\sum_j e^{f_j} }\]
만약 cross-entropy 함수를 사용하게 된다. Y target 값은 정답에만 1을 가지고 나머지 값들은 0을 가지게 된다
개인적인 생각으로 cross-entrpy 0을 곱하는 과정이나 위에 softmax loss \(-\log(y_i)\) 결론은 같다.
스케일에 대한 문제가 있다. Numeric stabilty 관점에서는 큰값을 나누면 불안정하다
그래서 C는 score 최댓값을 구해 score에서 빼준다.
1.2 \(L\) + reg
\[L = \underbrace{ \frac{1}{N} \sum_i L_i }_\text{data loss} + \underbrace{ \lambda R(W) }_\text{regularization loss} \\\\\]
소개에서 봤던 \(-\log(y_i)\) 수식은 각 데이터들에 대한 손실도 였기 때문에
전체 데이터 손실을 구해야한다.
데이터 손실 부분을 먼저 구하고 \(\underbrace{ \frac{1}{N} \sum_i L_i }_\text{data loss}\)
규제에 대한 손실값도 추가해야한다.\(\underbrace{ \lambda R(W) }_\text{regularization loss}\)
규제 방식은 이전에 사용했던 L2 규제를 사용하기 때문에 모든 가중치에 제곱하고 더한다\(\lambda \sum_k\sum_l W_{k,l}^2\)
2. train
2.1 softmax loss naive
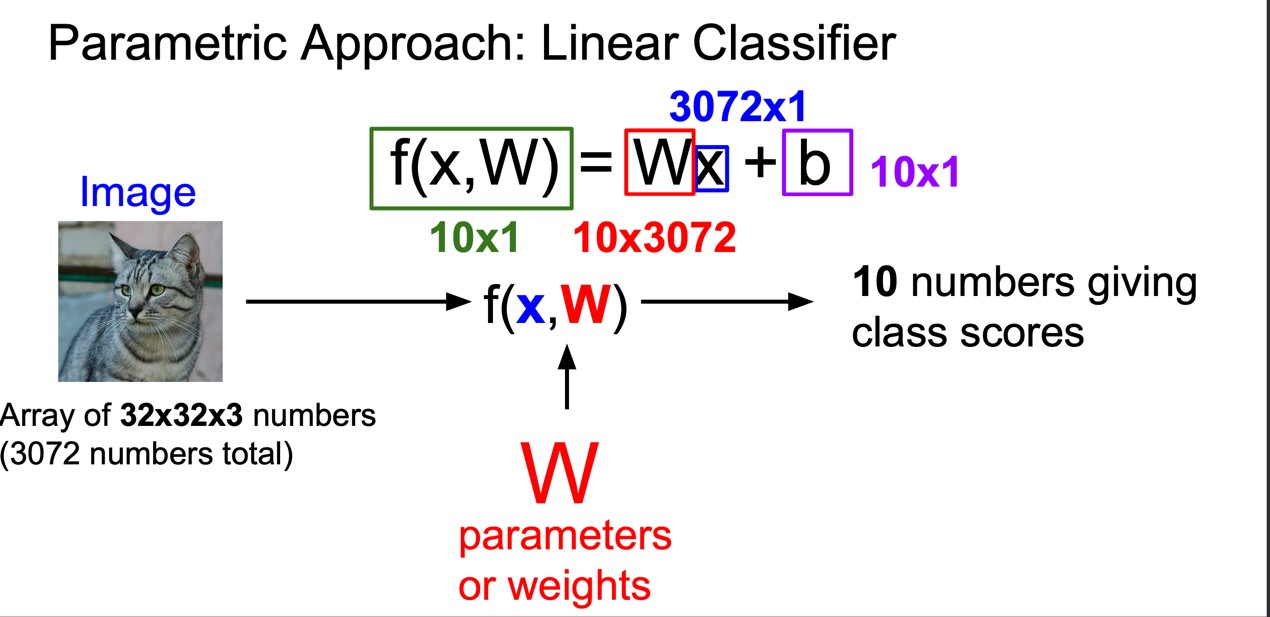
먼저 linear classifier \(W * x + b\) 사용해 class scores 설정해야한다.
각각 파아미터는 \(W\), \(x\), \(b\) 파리미터롤 사용이 될것이다.
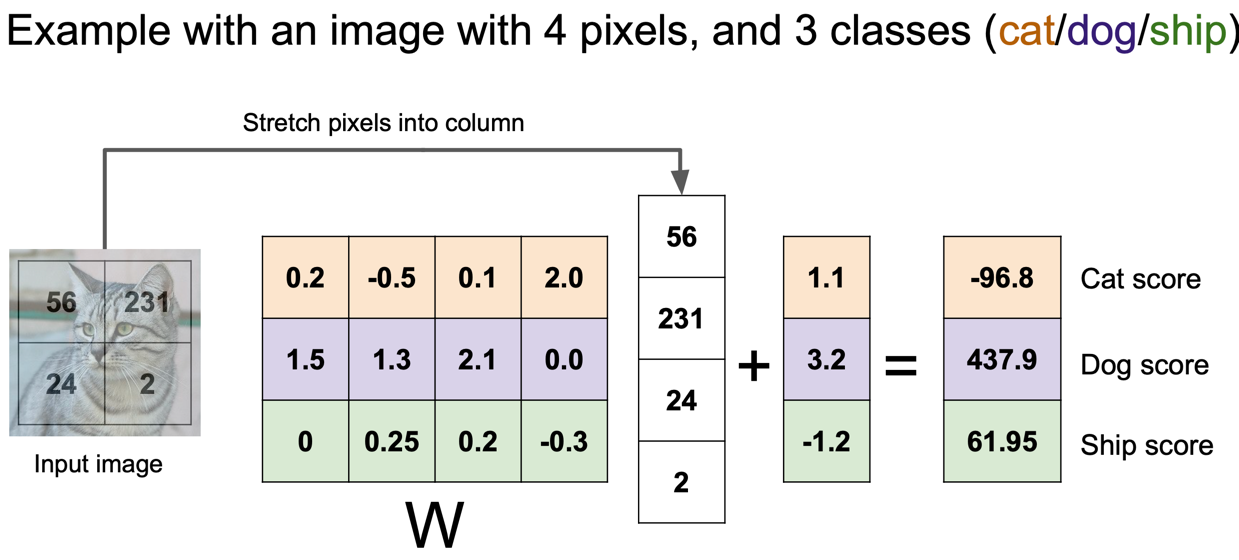
최종 적인 class scores 받는 그림이다.
이제 최적에 값을 찾아 가기위해서 Loss function 사용해 W 값을 업데이트 시킨다.
W 값에 최적에 값을 찾아가는 방식은 경사하강법을 사용하게된다. (미분한다!)
cnt = 0
for i in range(num_train):
wx = X[i].dot(W)
wx = wx - np.max(wx)
score = np.exp(wx)
# softmax 200 by 10
softmax = score / np.sum(score)
loss += -np.log(softmax[y[i]])
for j in range(num_classes):
dW[:, j] += softmax[j] * X[i]
dW[:, y[i]] -= X[i]
loss /= num_train
dW /= num_train
loss += reg * np.sum(W * W)
dW += 2 * reg * W
- wx = X[i].dot(W) : scores 점수를 계산한다.
- wx = wx - np.max(wx) : score 점수에서 최댓값을 빼 정규화 시킨다.
- score = np.exp(wx) : 모든 값을 exp 지수화 시킨다.
- softmax = score / np.sum(score) : 행 데이터 기준으로 더하고 해당 정답 score 나누게 한다.
- loss += -np.log(softmax[y[i]]) : Loss 구한다.

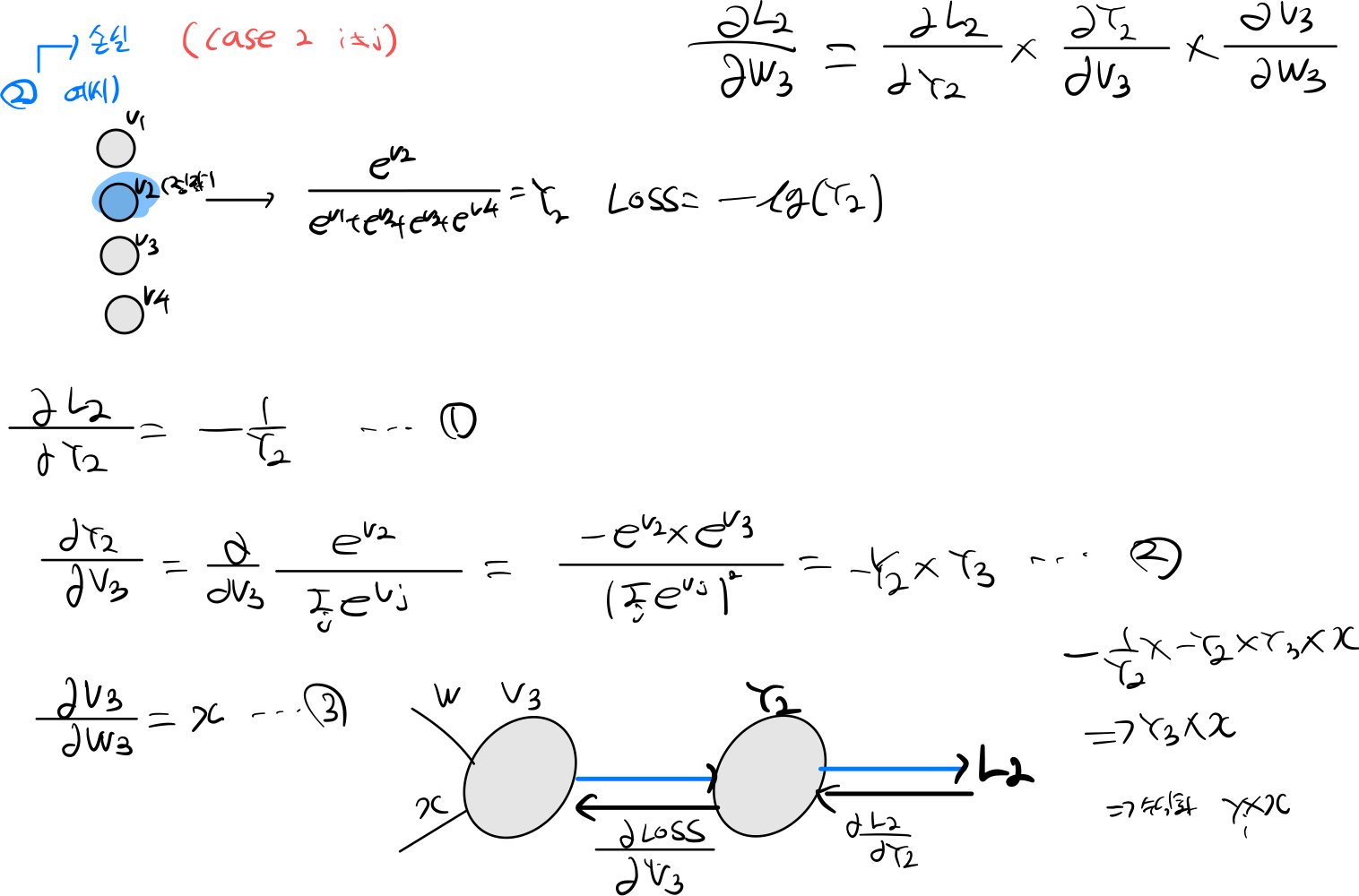
2.2 softmax dx
W를 찾아가는 미분방식은 2가지가 존재한다. 정답을 미분하는 경우, 정답외에 다른것을 미분하는 경우로 나누게 된다.

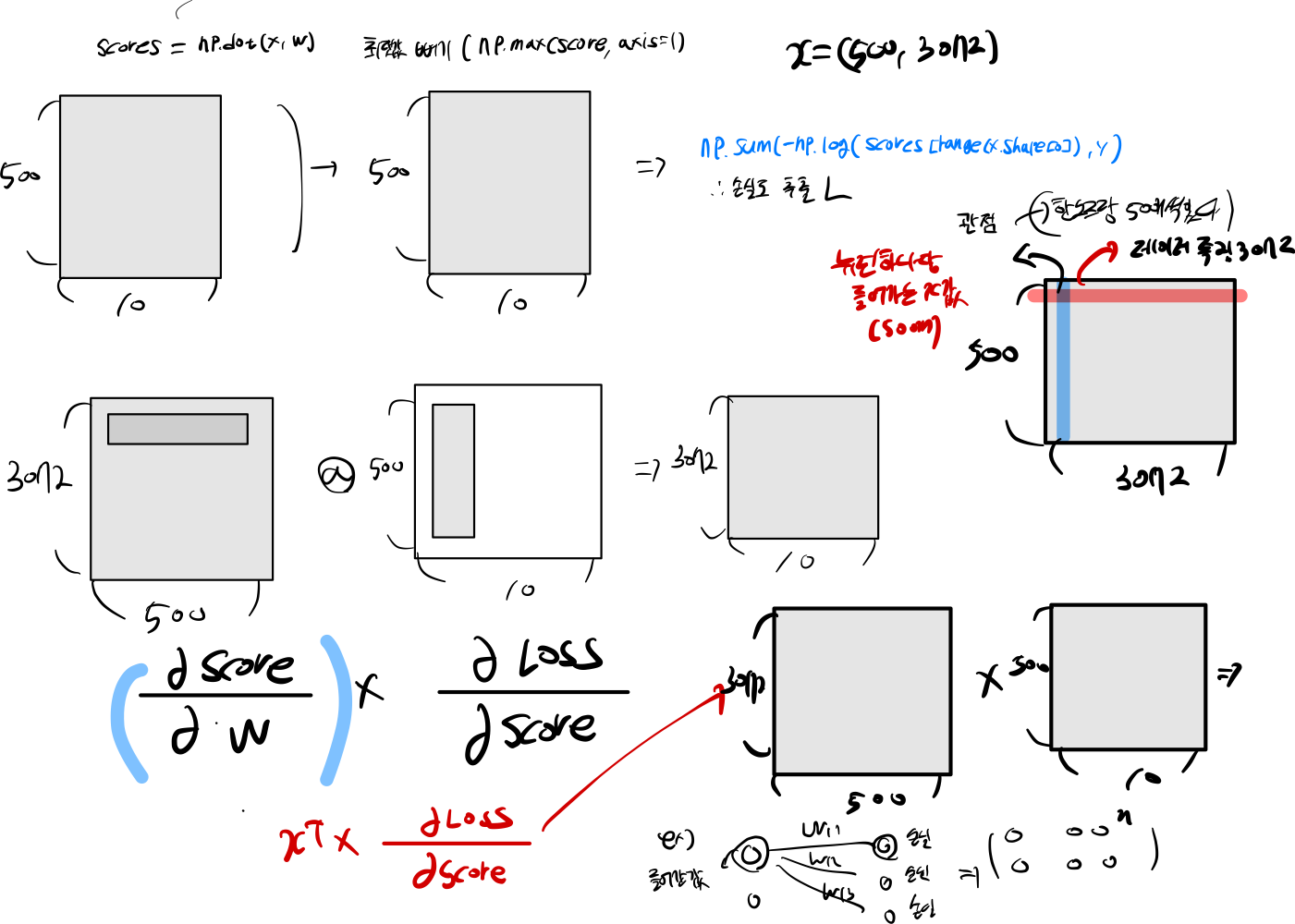
2.3 softmax loss vectorized
score = np.dot(X,W)
score -= np.max(score, axis=1).reshape(-1 ,1)
score = np.exp(score) / np.sum(np.exp(score), axis=1, keepdims=True)
loss = np.sum(-np.log(score[range(X.shape[0]), y]))
loss = loss / X.shape[0] + reg * np.sum(W ** 2)
score[range(X.shape[0]), y] -= 1
dW = X.T.dot(score) / X.shape[0] + 2 * reg * W
3. Question
Q : 3.1 Why do we expect our loss to be close to -log(0.1)? Explain briefly.**
# Generate a random softmax weight matrix and use it to compute the loss.
W = np.random.randn(3073, 10) * 0.0001
loss, grad = softmax_loss_naive(W, X_dev, y_dev, 0.0)
# As a rough sanity check, our loss should be something close to -log(0.1).
print('loss: %f' % loss)
print('sanity check: %f' % (-np.log(0.1)))
loss: 2.310496
sanity check: 2.302585
- 현재 가중치 초기화 값이 0에 가깝기 때문에 초기에는 모든 값이 0에 가까워질 것으로 예상됩니다. 이에 따라 10개의 클래스를 분류하는 작업에서 각 클래스의 점수가 모두 0에 가깝게 나올 것으로 예상합니다. Softmax 함수를 사용하여 클래스 점수를 확률 분포로 변환하면, 모든 확률의 합이 1이 되어야 합니다. 따라서 각 클래스에 대한 예상 확률은 1/10, 즉 0.1이 될 것으로 예상됩니다.
Q : 3.2 Suppose the overall training loss is defined as the sum of the per-datapoint loss over all training examples. It is possible to add a new datapoint to a training set that would leave the SVM loss unchanged, but this is not the case with the Softmax classifier loss.
- 만약 정말 중요한 data point는 손실을 개선 하지만, 평균 혹은 미미한 특징이라면 SVM 큰 개선이 이루어지지않는다. 왜냐 하면 ((margin + score) - 정답 ) 공식을 사용하기 때문에 계속 정답이 음수이면 손실 개선이 없다.하지만 softmax 최대한 1에 까가워 질수 있도록 개선을 하기 때문에 하나의 작은 특징이라도 들어온다면 계속해서 개선을 할 것이다.