과제1. Two Layer Neural Network
cs231n 과제1. Two Layer Neural Network 정리
Two Layer Neural Network
1. introduce
신경망은 생물학적인 신경 시스템을 모델링하는 데 영감을 받아 개발되었습니다. 이제 이 소개에서는 코드 상에서 신경망이 어떻게 학습되는지에 초점을 맞추어 설명하겠습니다.
생물학적인 신경 시스템에서 영감을 받은 신경망은 인공 뉴런으로 구성되어 있습니다. 이러한 뉴런들은 수많은 연결로 연결되어 정보를 전달하고 처리합니다. 이와 유사하게, 인공 신경망은 여러 개의 뉴런 또는 노드로 구성되며, 이 노드들은 서로 연결되어 데이터를 처리합니다.
인공 신경망이 학습하는 과정은 크게 두 단계로 나눌 수 있습니다. 첫 번째 단계는 순전파(forward propagation)로, 입력 데이터가 네트워크를 통해 전달되며 각 뉴런은 가중치와 활성화 함수를 사용하여 데이터를 처리하고 출력을 생성합니다. 이렇게 생성된 출력은 실제 정답과 비교하여 오차를 계산합니다.
두 번째 단계는 역전파(backpropagation)로, 이 오차를 최소화하기 위해 네트워크의 가중치와 편향을 조정합니다. 역전파는 오차를 출력층에서 시작하여 입력층으로 거꾸로 전파하면서 각 뉴런의 가중치에 대한 오차 기여도를 계산합니다. 이 오차 기여도를 사용하여 가중치와 편향을 업데이트하고, 이 과정을 여러 번 반복하여 네트워크가 학습됩니다.
이렇게 학습된 신경망은 입력 데이터에 대한 패턴을 학습하고, 새로운 데이터에 대한 예측을 만들 수 있습니다. 이러한 학습 과정을 통해 인공 신경망은 다양한 작업, 예를 들면 이미지 분류, 자연어 처리, 게임 플레이, 로봇 제어 등 다양한 응용 분야에서 사용됩니다.
2 Architectures
2.1 Layer-wise organization
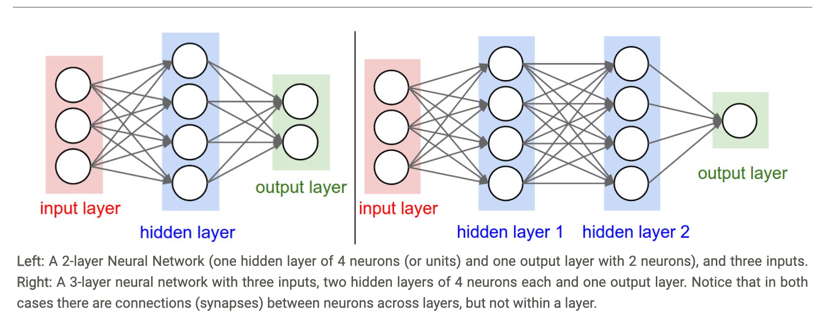
레이별로 구성이 따로 있다 입력을 받는 레이어는 input-layer 결과을 출력하는 layer output-layer 입력과 결과를 연결해주는 hidden-layer 구성한다.
input, output, hidden 모두 계층형태로 연결되어있는 형태이다.
주의할 점은 일부 뉴런의 출력이 다른 뉴런의 입력으로 사용될 수 있습니다.
2.2 Naming conventions
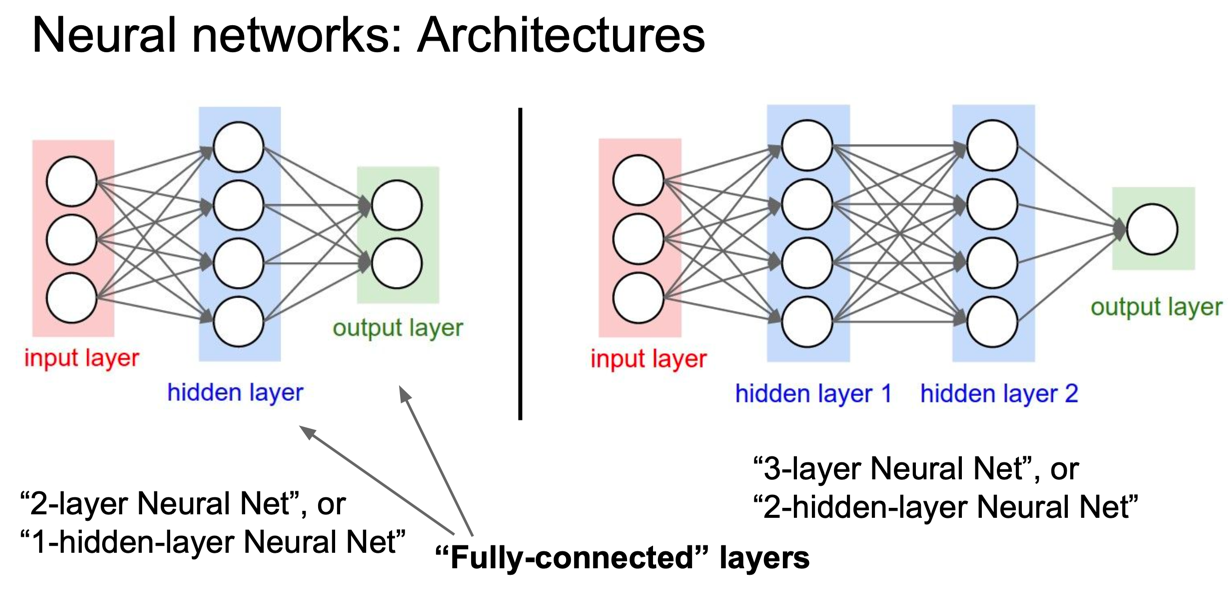
Input 제외한 모든 신경망을 포함해서 불러야한다. 만약 입력 포함해서 3개의 layer 있다면 2-layer neural Net 사용해야한다 혹은 input, out 제외한 hidden-layer 부르는 1-hidden-layer neural net 불러진다.
2.3 Output layer.
출력 신경망에는 일반적으로는 활성화 함수 기능이 없습니다. 왜냐하면 일반적으로 클래스 점수를 나타내기 위해 사용하기 때문입니다. 클래스의 임의의 실제 값이거나, 실제 대상합니다.
3. train
3.1 affine_forward
input_size = x.shape[0]
data = x.reshape(input_size, -1)
out = (data @ w) + b
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
cache = (x, w, b)
return out, cache
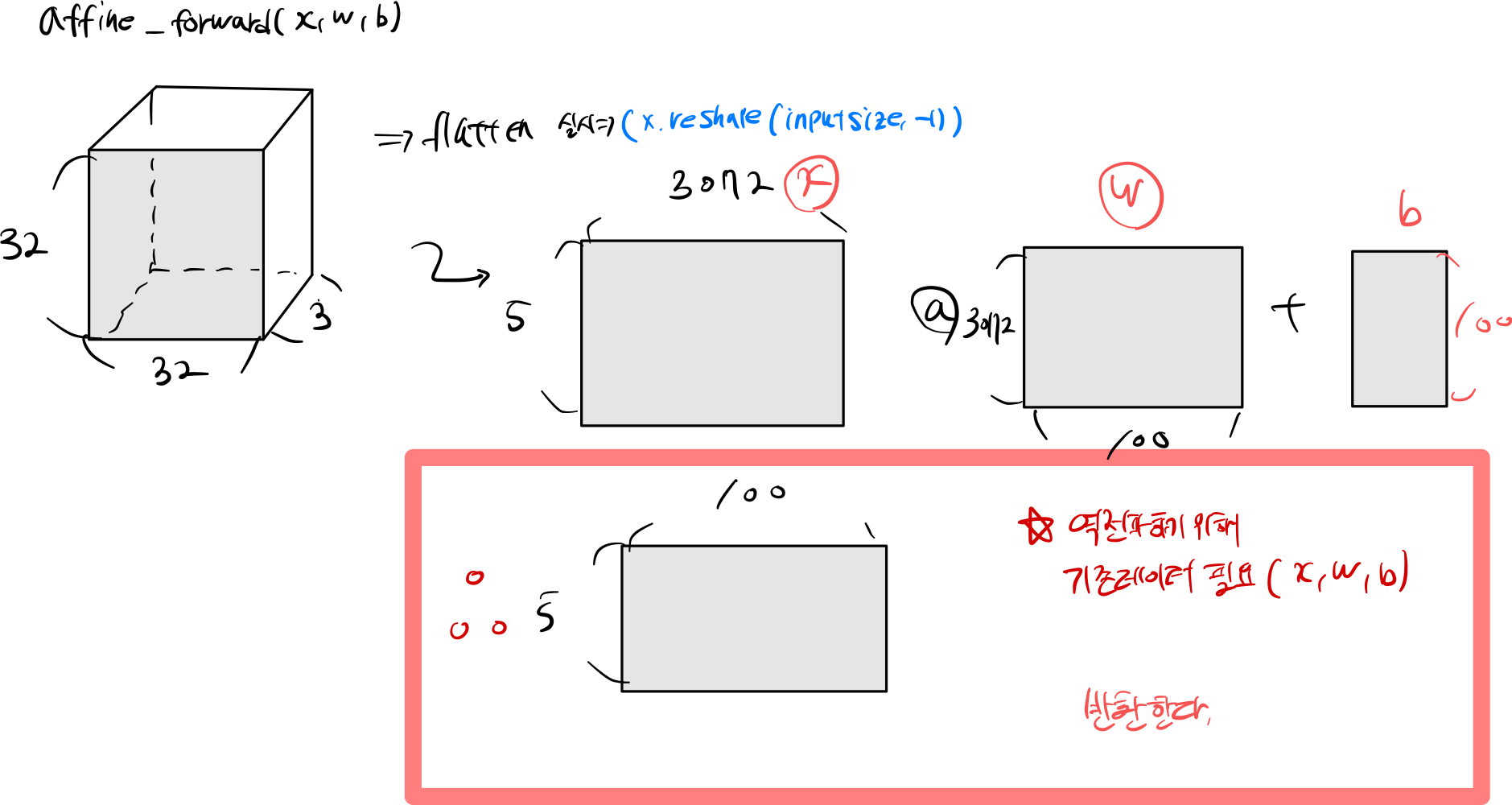
input_size = x.shape[0] : 입력 받은 이미지 전체 구하기
data = x.reshape(input_size, -1) : 데이터 feature flatten 실시
out = (data @ w) + b 내적 구하기
3.2 affine_backward
x, w, b = cache
dx, dw, db = None, None, None
###########################################################################
# TODO: Implement the affine backward pass. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
input_size = x.shape[0]
dw = (x.reshape(input_size, -1).T @ dout)
dx = (dout @ w.T).reshape(x.shape)
db = dout.sum(axis=0)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dw, db
x, w, b = cache : forward 사용했던 x, w, b 값을 가져온다.
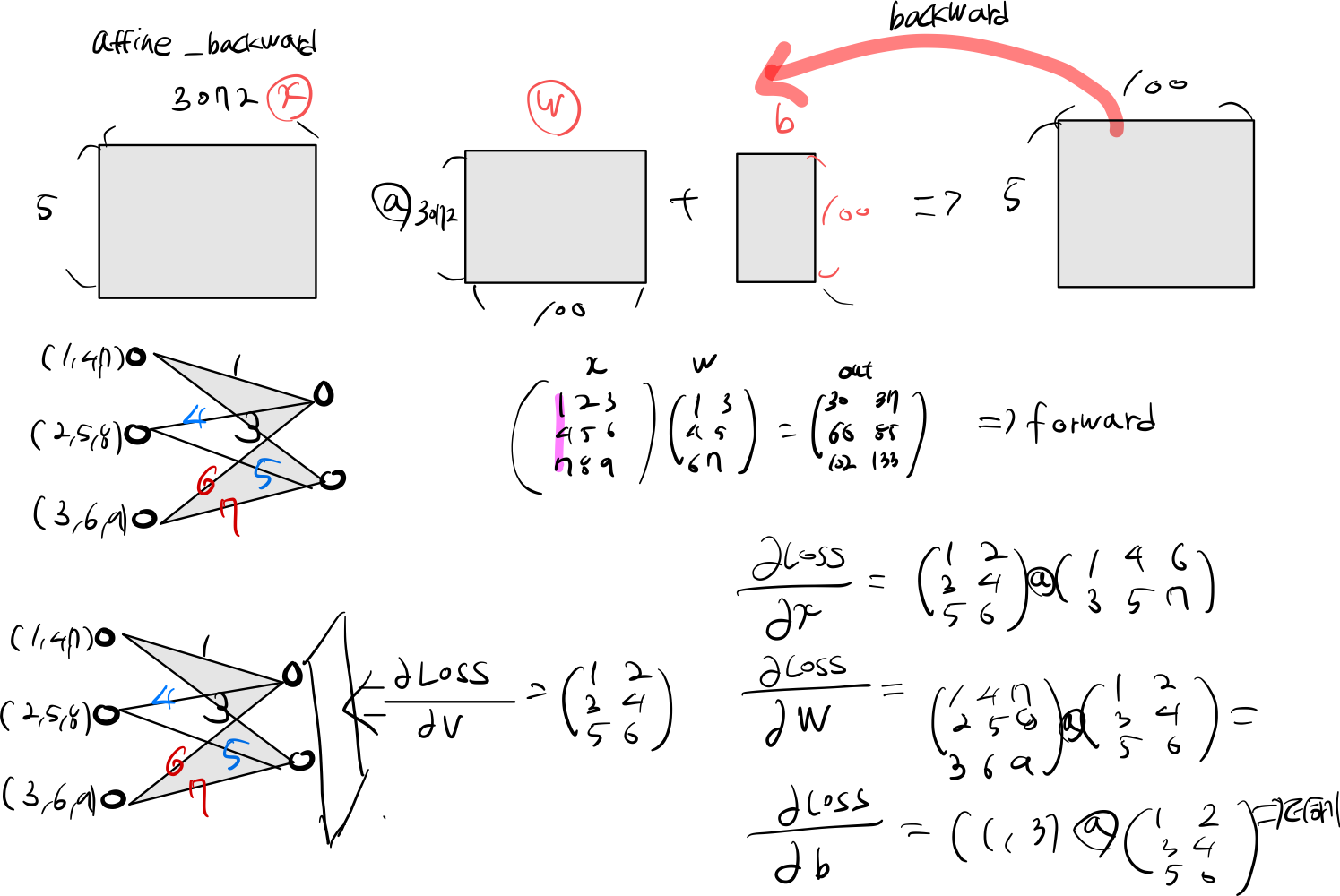
dw = (x.reshape(input_size, -1).T @ dout) : 편미분을 사용하여 dw 가중치 업데이트 한다 자세한 설명은 밑에 그림을 보면 참고하자
dx = (dout @ w.T).reshape(x.shape) : 편미분을 사용하여 dx 가중치를 업데이트 한다.
db = dout.sum(axis=0) : dout node에 대한 손실값을 node 단위로 계산하다.
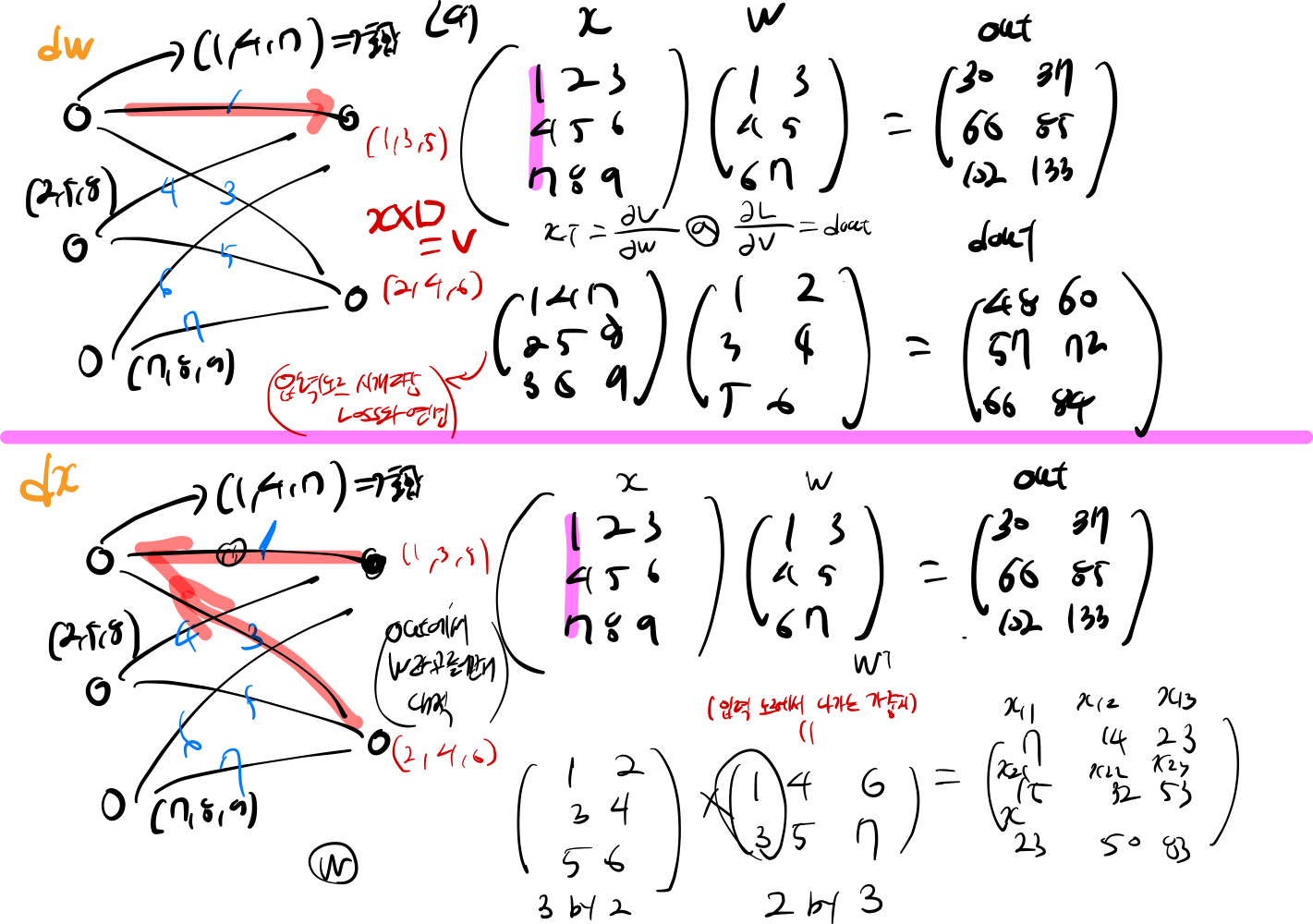
input = np.array([
[1,2,3],
[4,5,6],
[7,8,9]
])
w = np.array([
[1,3],
[4,5],
[7,8]
])
out = input @ w
dout = np.array([
[1,2],
[3,4],
[5,6]
])
print(input.T @ dout)
print(dout @ w.T)
dw 업데이트 :
[[48 60]
[57 72]
[66 84]]
dx 업데이트 :
[[ 7 14 23]
[15 32 53]
[23 50 83]]
역전파 하는 과정을 간단하게 코드로 구현
3.3 relu forward
out = np.maximum(0, x)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
cache = x
return out, cache
out = np.maximum(0, x) : 들어온 값들을 0이하면 0으로 만들고 초과한 값은 x 값을 사용한다.
3.3 relu forward
out = np.maximum(0, x)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
cache = x
return out, cache
out = np.maximum(0, x) : 들어온 값들을 0이하면 0으로 만들고 초과한 값은 x 값을 사용한다.
3.4 relu backward
###########################################################################
# TODO: Implement the ReLU backward pass. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x[x > 0] = 1
x[x <= 0] = 0
dx = dout * x
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx
x[x > 0] = 1 : 0 초과 값은 1 초기화 한다. x[x <= 0] = 0 : 0이하 값은 0으로 초기화 한다.

3.4 TwoLayerNet 신경망 구축하기
3.1 ~ 3.3까지는 신경망이 동작하는 방식을 구축했다면
이번에는 신경망을 구축하는지 코드화 할 것이다.
W1 = np.random.randn(input_dim, hidden_dim) * weight_scale
W2 = np.random.randn(hidden_dim, num_classes) * weight_scale
b1 = np.zeros((1, hidden_dim))
b2 = np.zeros((1, num_classes))
self.params['W1'] = W1
self.params['W2'] = W2
self.params['b1'] = b1
self.params['b2'] = b2
W1 = np.random.randn(input_dim, hidden_dim) * weight_scale : 가중치를 초기화 하는 작업, weight_scale 가중치 스케일을 조정하는 작업(W2 같음) b1 = np.zeros((1, hidden_dim)) : bias 초기화 뉴런의 갯수 만큼
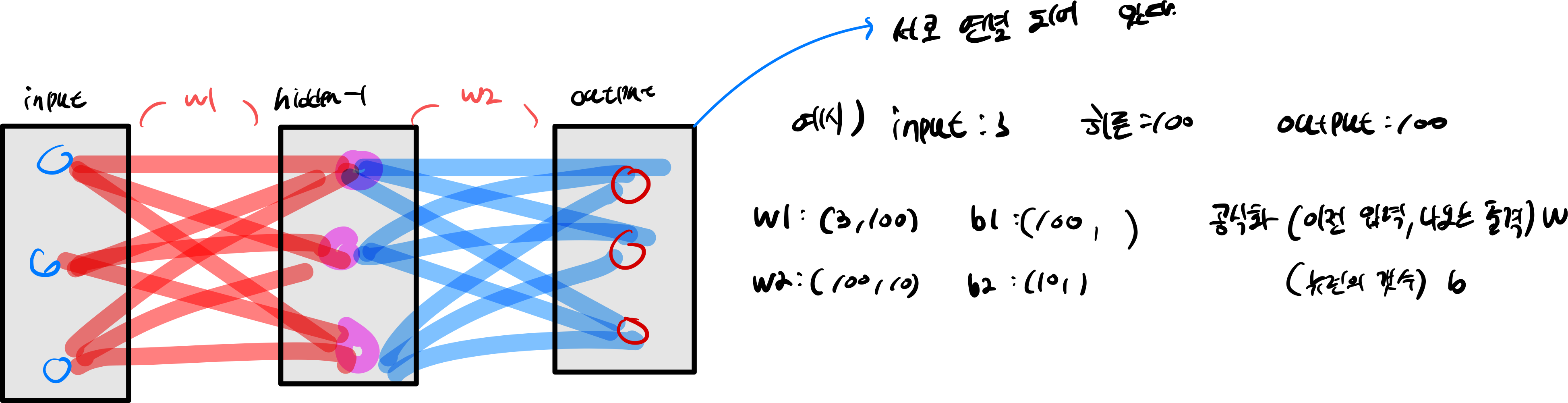
3.5 TwoLayerNet forward, backward, loss
model 만들고 forward, backward, loss 구하는 과정을 코드로 구현한다.
W1 = self.params['W1']
b1 = self.params['b1']
W2 = self.params['W2']
b2 = self.params['b2']
out1, cache1 = affine_relu_forward(X, W1, b1)
score, cache2 = affine_forward(out1, W2, b2)
scores = score
out1, cache1 = affine_relu_forward(X, W1, b1) : input date, hidden data forward 시킨다. score, cache2 = affine_forward(out1, W2, b2) : hidden layer, output layer forward 시킨다. 주의할 점은 모든 X, w, b 값들으 cache 값으로 저장해야 한다.
loss, dx = softmax_loss(score, y)
loss += 0.5 * self.reg * ((W1 * W1).sum() + (W2 * W2).sum())
dx, grads['W2'], grads['b2'] = affine_backward(dx, cache2)
dx, grads['W1'], grads['b1'] = affine_relu_backward(dx, cache1)
grads['W1'] += self.reg * W1
grads['W2'] += self.reg * W2
3. Question
Q : 3.1 We’ve only asked you to implement ReLU, but there are a number of different activation functions that one could use in neural networks, each with its pros and cons. In particular, an issue commonly seen with activation functions is getting zero (or close to zero) gradient flow during backpropagation. Which of the following activation functions have this problem? If you consider these functions in the one dimensional case, what types of input would lead to this behaviour?
- Sigmoid
- ReLU
- Leaky ReLU
Sigmoid 문제점 3가지
- exp 계산 비용이 오래건린다.
- 모든 값들이 양수를 가진다.(sigmoid 값의 최솟값은 0이상의 값을 가지게 된다. 역전파를 진행하게 된다면 sigmoid 함수를 사용하는 뉴런은 항상 양수 혹은 음수를 가지게된다.)
- 값들 최대 / 최소로 값을 가진다면 기울기가 손실되는 현상이 발생한다. (sigmoid 미분하게 된다면 0에서 극대값을 가지고, 값이 커지거나, 값이 작아질 수록 기울기가 0으로 수렴하는 현상을 알 수 있다.)
Relu 문제점 1가지
- 입력 값이 음수라면 기울기가 0이 되는 현상이 발생한다.
Q : 3.2 Now that you have trained a Neural Network classifier, you may find that your testing accuracy is much lower than the training accuracy. In what ways can we decrease this gap? Select all that apply.
- Train on a larger dataset.
- Add more hidden units.
- Increase the regularization strength.
- None of the above.
- 훈련데이터가 작은 집단을 사용하게 된다면, 해당 집단에 맞는 데이터만 훈련하게 될 것이다. 만약 다른 특징에 data 예측하고 싶다면,정답과 다른 값을 예측할 것이다. 왜냐하면 가중치를 학습을 했을 때에는 기존에 있는 data 사용해서 최적에 W 업데이트 했기 떄문이다.
- 만약 train data 딱 맞게 학습이 된다면, 훈련 데이터 이외에 사용할 수 없는 모델이 된다. 그래서 너무 과하게 훈련을 막기위해 가중치를 규제를 걸어 훈련에 과적합을 막지만, 반대로 약하게 규제를 설정한다면 과적합이 발생한다.
참조
- https://cs231n.github.io/