4 분 소요

배치 정규화 코드 구현

1. Introduce

신경망을 학습하는데 문제점을 흔하게 발생하는 문제점이 Vanishing, Exploding 발생한다. 잘 사용하지 않지만, 설명하기 좋은 Relu 함수를 가지고 설명을 한다면

Relu 값은 음수로 값이 가게 된다면 모든 값이 0이 된다. 그 상태로 backpropagation 실행한다면, \(dw = X * \frac{dLoss}{dv}\) X 값들은 모두 0이 될것이다. 그럼 역전파가 제대로 발생하지 않을 것이다.

반대로 Exploding 값이 된다면 \(dw = X * \frac{dLoss}{dv}\) X 큰값을 가지기 때문에 값이 폭팔하게 될것이다.

이것을 해결하기 가중치를 적절하게 초기화 해야하지만, 결국 layer 지날수록 값들은 0으로 수렴하게 될것이다. (Xavier 초기화 또는 He 초기화 한다면 문제를 그나마 해결할 수 있음) 그래서 해결 방법으로 Batch Normalization 논문이 나오게 되었다.

Batch Normalization 사용방법은 아래와 같은 계산법을 사용하게 된다.

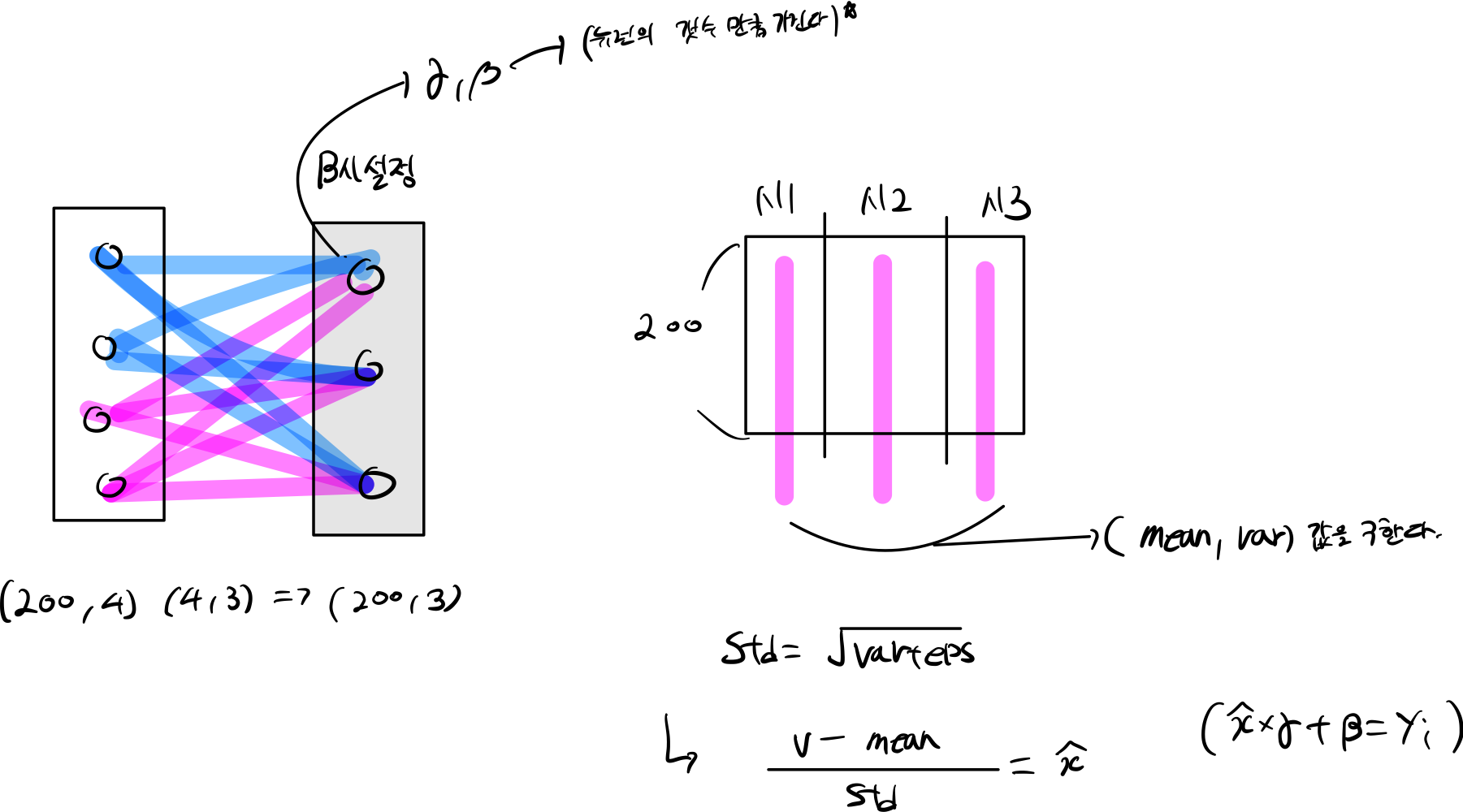
\(\begin{align} & \mu=\frac{1}{N}\sum_{k=1}^N x_k & v=\frac{1}{N}\sum_{k=1}^N (x_k-\mu)^2 \\ & \sigma=\sqrt{v+\epsilon} & y_i=\frac{x_i-\mu}{\sigma} \\ & y_i = \gamma*y_i + \beta \end{align}\) kyumly

2. Batch Norm Forward

2.1 forward 과정

2.1.1 원리

  1. 뉴런당 해당하는 평균 값을 구한다.
  2. 분산을 구하고
  3. 표준편차 =분산 + eps 구한다.
  4. 정규분포를 구해
  5. gamma, beta 추가해준다.

2.1.2 code

def batchnorm_forward(x, gamma, beta, bn_param):

    mode = bn_param["mode"]
    eps = bn_param.get("eps", 1e-5)
    momentum = bn_param.get("momentum", 0.9)

    N, D = x.shape
    running_mean = bn_param.get("running_mean", np.zeros(D, dtype=x.dtype))
    running_var = bn_param.get("running_var", np.zeros(D, dtype=x.dtype))

    out, cache = None, None
    if mode == "train":

        x_mean = np.mean(x, axis=0)
        var = np.var(x, axis=0)

        std = np.sqrt(var + eps)
        x_hat = (x - x_mean) / std
        out = gamma * x_hat + beta

        shape = bn_param.get('shape', (N, D))
        axis = bn_param.get('axis', 0)

        cache = x, x_mean, var, std, gamma, x_hat, shape, axis # save for backprop

        if axis == 0:
            running_mean = momentum * running_mean + (1 - momentum) * x_mean # update overall mean
            running_var = momentum * running_var + (1 - momentum) * var  # update overall variance

    elif mode == "test":
        x_hat = (x - running_mean) / np.sqrt(running_var + eps)
        out = gamma * x_hat + beta

    else:
        raise ValueError('Invalid forward batchnorm mode "%s"' % mode)

    bn_param["running_mean"] = running_mean
    bn_param["running_var"] = running_var

    return out, cache

2.2 backward 과정

2.2.1 원리


밑에 그림은 backpropagation 진행하는 과정을 표시했다.

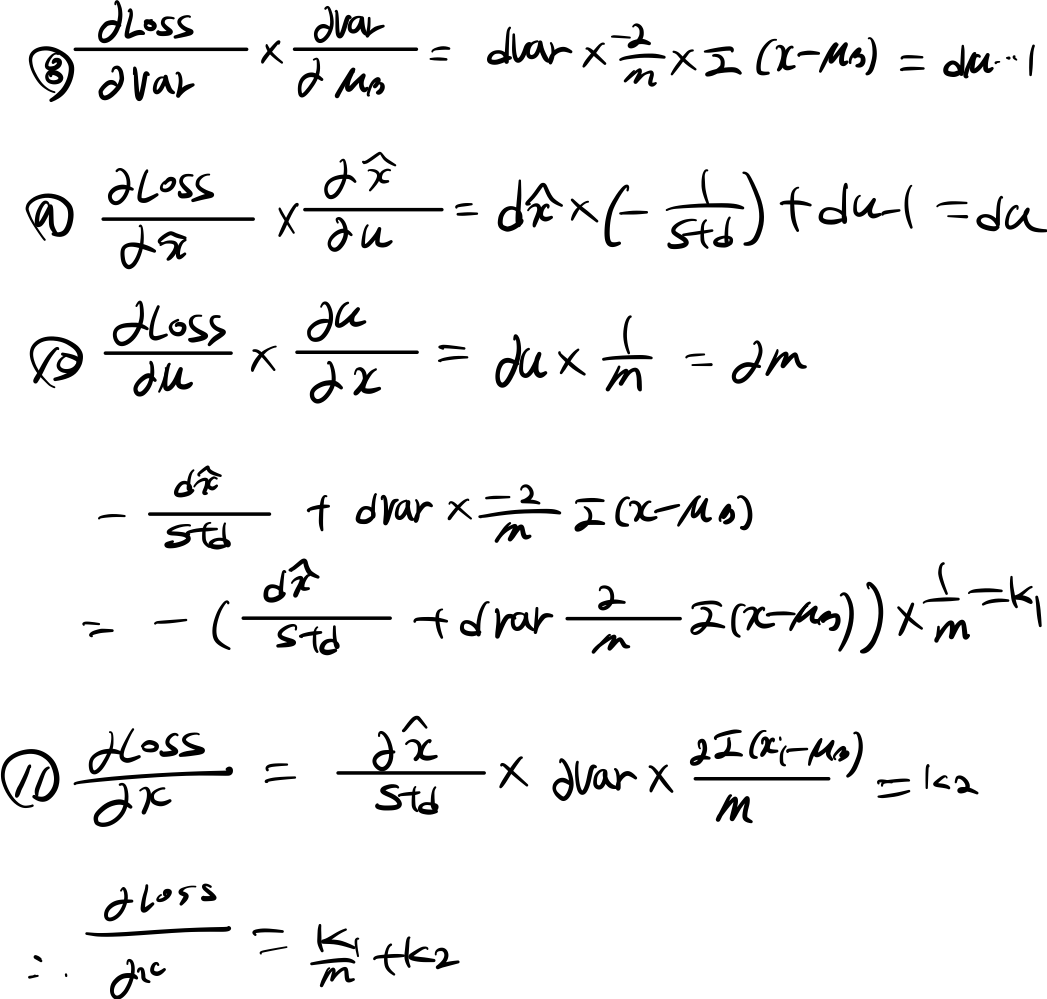
kyumly
kyumly

2.2.2 code

def batchnorm_backward(dout, cache):
    x, mu, var, std, gamma, x_hat, shape, axis = cache

    dbeta = dout.sum(axis=0)
     
    dgamma = (dout * x_hat).sum(axis=0)

    dx_hat = dou t * gamma

    dstd = -np.sum(dx_hat * (x-mu), axis=0) / (std**2)

    dvar = 0.5 * dstd / std

    dx_1 = dx_hat / std

    dx_2 = 2 * (x - mu) * dvar / len(dout)

    dx_k1 = dx_1 + dx_2

    dmu = -np.sum(dx_k1, axis=0)  # derivative w.t.r. mu

    dx_k2 = dmu / len(dout)  # partial derivative w.t.r. dx

    dx = dx_k1 + dx_k2

    return dx, dgamma, dbeta

2.2.3 backnorm alt

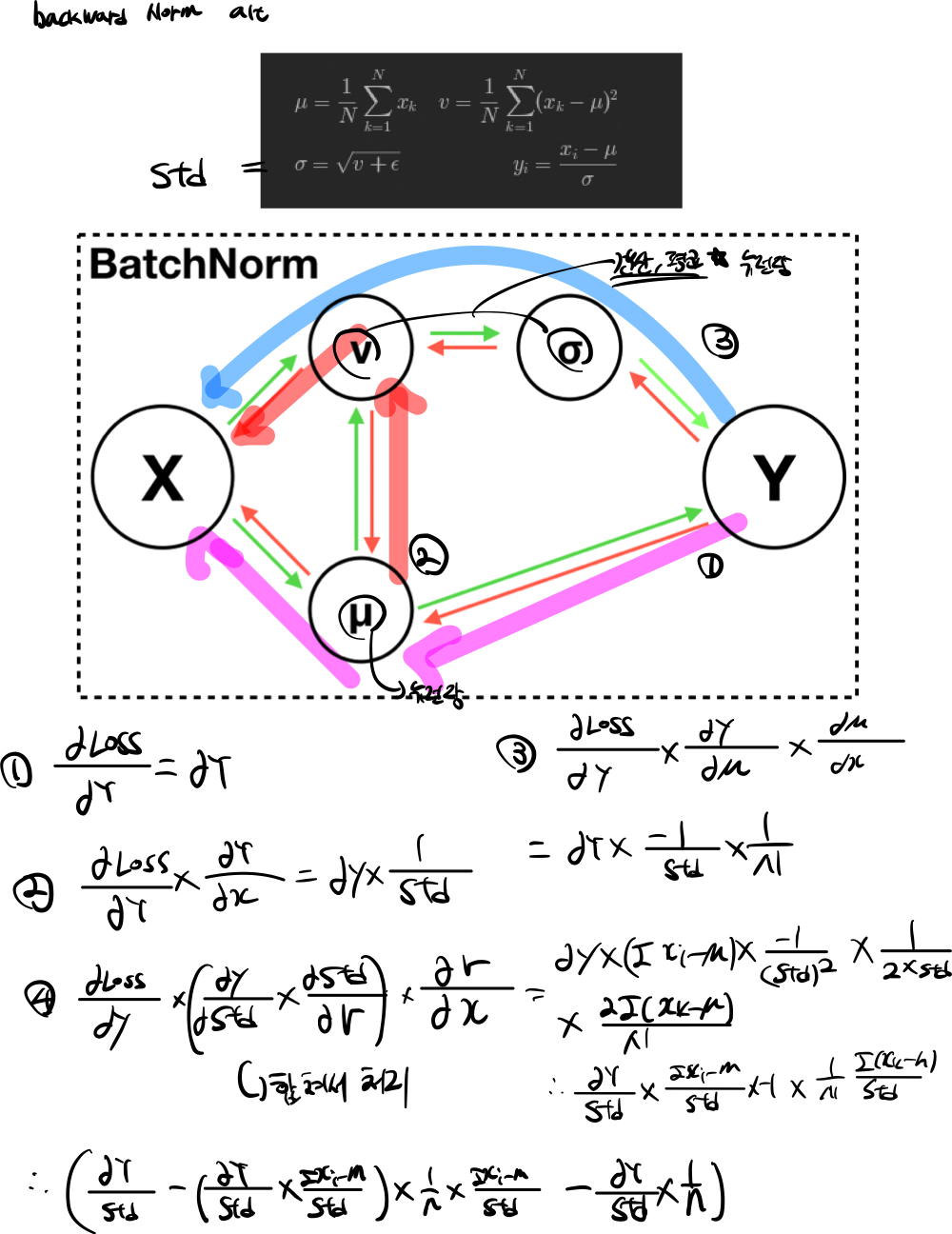
kyumly kyumly

def batchnorm_backward_alt(dout, cache):
    dx, dgamma, dbeta = None, None, None

    _, _, _, std, gamma, x_hat, shape, axis = cache  # expand cache

    dbeta = dout.sum(axis=axis)
    dgamma = (dout * x_hat).sum(axis=axis)

    dx_hat = dout * gamma
    N = len(dout)

    dx = dx_hat / std

    dx = dx - (((dx * x_hat).sum(axis=0) * x_hat) / N) - (dx.sum(axis=0) / N)

    return dx, dgamma, dbeta

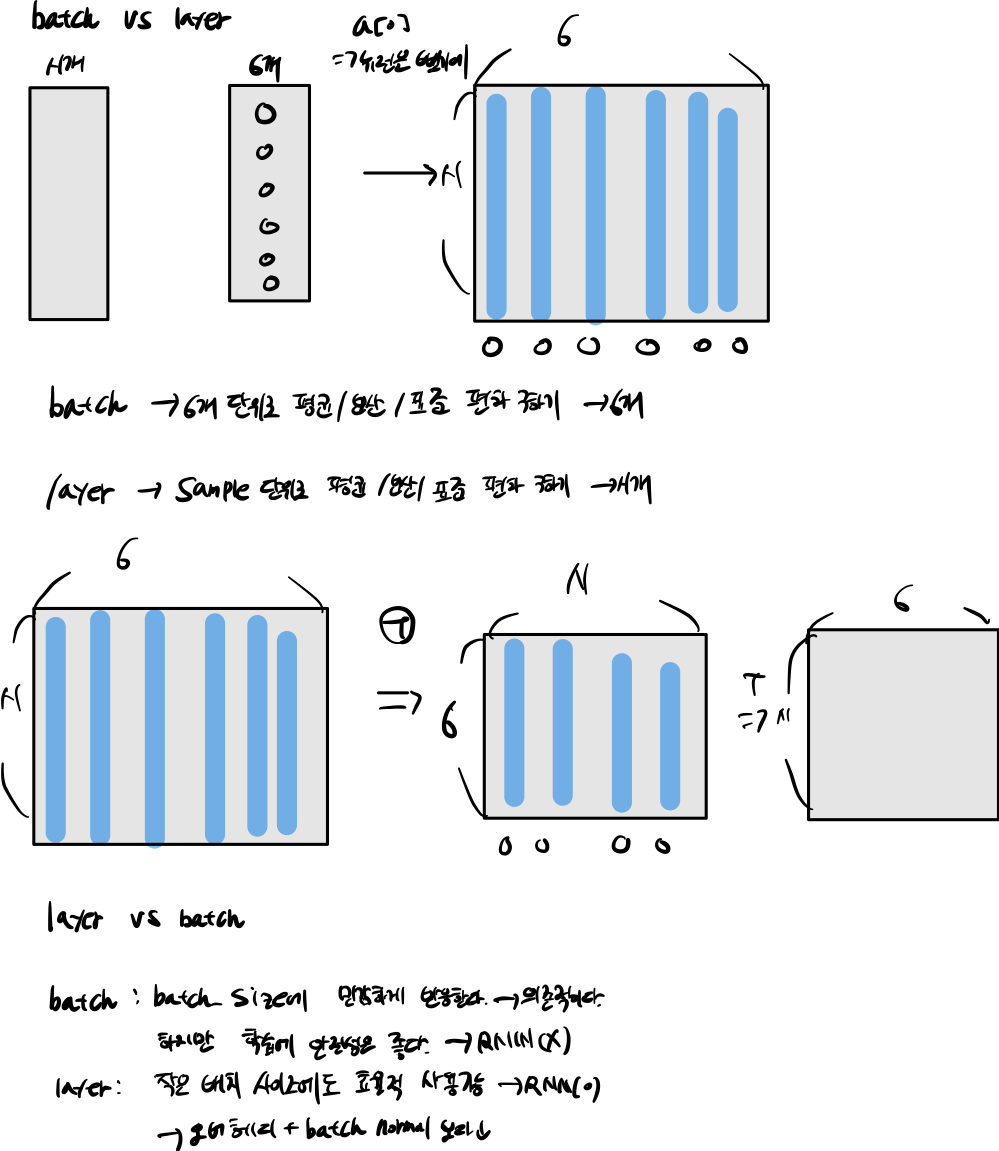
3 layer-normal

batch Normal 에서는 batch-size 너무 의존적이다. 위에 증명과 수식을 봤을 때 batch 사이즈로 뉴런의 평균, 표준 편차를 구하게 된다
그래서 나온 방법이 layer-normal 방식이다.

layer-normal 방식은 layer 기준으로 평균과 분산을 구하게 된다. 즉 batch-normal 반대되는 성질을 가지고 있다.

kyumly

4. Question

4.1 Question 1

Describe the results of this experiment. How does the weight initialization scale affect models with/without batch normalization differently, and why?

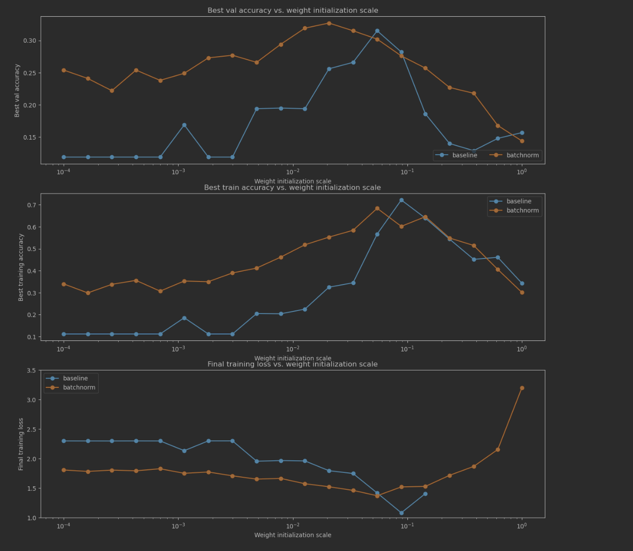
kyumly

4.1.2 Answer 1

정확도

  • 전체적인 정확도를 살펴보면 정규화 했을시 더 좋은 정확도를 나타내고 있다.
  • 왜냐하면 가중치가 너무 작거나, 너무작거나, 너무 크면 vanishing, Exploding 문제가 발생한다.
  • 예를 들어 가중치 값이 너무 작으면, backpropagation dx = local grad(x) * upstream(미분값) 하게된다면, w값이 작기 때문에 모든 활성화 함수는 0으로 갈것이다.
  • 문제를 해결하는 방식으로 BN을 사용해서 모든 뉴런에 들어가는 값을 정규분포르 변경하여 값들을 정규화 시킨다.
  • 위에 그럼에 보이는 것처럼 가중치가 너무 작더라고 BN을 사용했기 때문에 정확도가 올라간것을 볼 수 있고, 반대로 BN 사용하지 않은 경우는 기울기 손실로 값들잉 좋은 정확도를 볼 일수없다.
  • 가중치가 너무 작으면 모든 확설화 함수 값은 0으로 가고, 반대로 너무 크면 기울기가 죽는 현상이 발생한다.

스케일 조정

  • 현재 가중치 10^-1 부분을 보면 특이한 지점을 볼 수 있다.
  • 10^-1 부분이 최적에 가중치 값을 찾았다고 볼 수 있다. 하지만 그 이후 높아진다면, 기울기 손실이 발생하기 때문에 조절해야한다.

4.2 Question 2

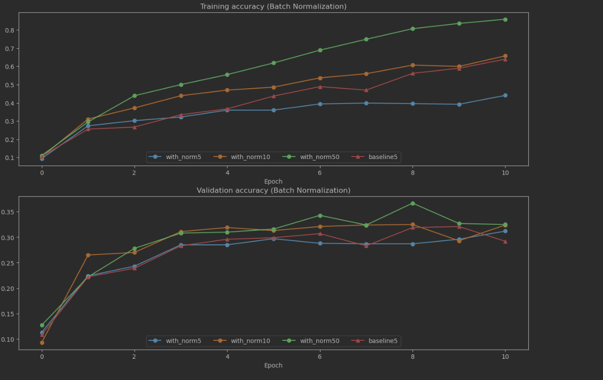
Describe the results of this experiment. What does this imply about the relationship between batch normalization and batch size? Why is this relationship observed? kyumly

4.2.2 Answer 2

  • 배치 사이즈가 더 많아 진다는 것은 표본이 더 많이 생긴다는 뜻이다.
  • 만약 배치 사이즈가 한개 밖에 안된다면, 위에 공식에 따르면 단일 뉴런만 받아진다.
  • 그럼 배치 사이즈가 크면 클수록 집단에 사이즈가 커진다는 것을 알수있다

4.3 Question 3

Which of these data preprocessing steps is analogous to batch normalization, and which is analogous to layer normalization?

  1. Scaling each image in the dataset, so that the RGB channels for each row of pixels within an image sums up to 1.
  2. Scaling each image in the dataset, so that the RGB channels for all pixels within an image sums up to 1.
  3. Subtracting the mean image of the dataset from each image in the dataset.
  4. Setting all RGB values to either 0 or 1 depending on a given threshold.

4.3.2 Answer:

  1. 2번은 layer-norm 대한 이야기 이다. layer는 전체 픽셀의 값을 이용하여 평균, 분산을 구하게 된다.
  2. 3번은 batch-norm 대한 이야기 이다. 각각에 dataset 기준으로 평균, 분산을 구한다음에 새로운 값을 구한다.

4.4 Question 3

When is layer normalization likely to not work well, and why?

  1. Using it in a very deep network
  2. Having a very small dimension of features
  3. Having a high regularization term

4.3.3 Answer:

  • 2,3 정답
    1. 차원이 적을 수 록 정규화할 표본들아 적아진다.

Additional references

  • https://cs231n.github.io

참고

cs231n & eecs498 Regularization and Optimization 교안 정리

3 분 소요

0. Last Time : Loss function quantify preferences 총 2개의 분류 Loss Function 공부했음 하지만 Training data 결과가 좋지만, Test Data 결과가 안좋은것을 확인할 수 있음 이번 강의에서는 Traini...