cs231n 강의 노트 9장 Convolutional Neural Networks
Convolutional Neural Networks 정리
pre. Convolutional Neural Networks (CNNs / ConvNets)
Convolutional Neural Networks are very similar to ordinary Neural Networks from the previous chapter: they are made up of neurons that have learnable weights and biases.
Each neuron receives some inputs, performs a dot product and optionally follows it with a non-linearity.
The whole network still expresses a single differentiable score function: from the raw image pixels on one end to class scores at theother.
And they still have a loss function (e.g. SVM/Softmax) on the last (fully-connected) layer and all the tips/tricks we developed for learning regular Neural Networks still apply.
- 컨볼루션 뉴런 비슷하다 이전에 배웠던 Ch.Neural Networks 똑같이 구성되어 학습 가능한 가중치와 편향이 있는 뉴런으로 구성되어 있음
- 각각 뉴런은 입력을 받아 내적을 계산하고 비 선형 구조를 따르고 있음 전체 네트워크는 미분 가능한 함수를 표현한다. 이미지 픽셀부터 Class score 까지임, 그리고 FC 연결된 손실함수를 가지고 있고 뉴런 네트워크를 개발하는데 필요한 팁/함정을 모두 가지고 있어 Neural Networks 똑같은 구조를 가지고 있음
So what changes? ConvNet architectures make the explicit assumption that the inputs are images, which allows us to encode certain properties into the architecture.
These then make the forward function more efficient to implement and vastly reduce the amount of parameters in the network.
- 변경된것은? Con 아키텍처는 입력값이 이미지라는 것을 명시적으로 가정한다. 그리고 특정 속성들은 아키텍처로 해석할 수 있도록 허락한다.
- 그런 다음 forward 함수를 더욱 통해 효과적으로 구현이 가능하고 많은 양에 network 파라미터들을 크게 줄일 수 있다. 이미지를 input으로 받고 forward 를통해 효과적으로 구현이 가능하며 파리미터 값을 줄일 수 있다.
1. Architecture Overview
Recall: Regular Neural Nets. As we saw in the previous chapter, Neural Networks receive an input (a single vector), and transform it through a series of hidden layers.
Each hidden layer is made up of a set of neurons, where each neuron is fully connected to all neurons in the previous layer, and where neurons in a single layer function completely independently and do not share any connections.
The last fully-connected layer is called the “output layer” and in classification settings it represents the class scores.
- 이전 챕터 Neural Nets에서 받아 input(단일 벡터) 인지하고, input 데이터를 hidden layer series 통해 변환했다.
- 각각에 hidden 층은 일련의 뉴런으로 구성되고, 각각 뉴런은 이전 뉴런들이랑 FC 연결되어 있으며 이러한 single layer 안에 있는 뉴런은 완전히 독립적으로 기능하고 연결을 공유하지 않는다.
- FC에 마지막에 있는 layer를 output layer 불러지며, 분류 설정에서 클래스 점수를 나타낸다.
Regular Neural Nets don’t scale well to full images.
In CIFAR-10, images are only of size 32x32x3 (32 wide, 32 high, 3 color channels), so a single fully-connected neuron in a first hidden layer of a regular Neural Network would have 32*32*3 = 3072 weights.
This amount still seems manageable, but clearly this fully-connected structure does not scale to larger images.
For example, an image of more respectable size, e.g. 200x200x3, would lead to neurons that have 200*200*3 = 120,000 weights.
Moreover, we would almost certainly want to have several such neurons, so the parameters would add up quickly!
Clearly, this full connectivity is wasteful and the huge number of parameters would quickly lead to overfitting.
- 일반적인 뉴런 네트워크는 전체 이미지와 스케일이 맞지 않는다.
- CIFAR-10 이미지는 32 * 32 * 3 가지고 있다. 그래서 신경만 첫번째 hidden layer에 완전히 연결된 단일 뉴런은 3072 가중치를 가지게 된다.
- 이러한 양은 관리할 수 있게 보이지만, FC 구조는 더 큰 이미지를 받을 수 없다.
- 예를 들어 아주 큰 이미지 구조인 200 * 200 *3 이면 120,000 가중치가 발생한다. 단일 뉴런은 120,000개의 가중치를 가지게 된다.
- 추가적으로 히든층 안에는 여러개의 뉴런이 발생하고 있기에 더 많아질 것이다.
-
분명히 이 FC는 낭비이며 엄청난 수의 매개변수는 빠르게 과적합으로 초래할 것이다.
- Image 스케일링이 안맞기 때문에 FC하기에는 무리가 있음 그래서 과적합이 발생한다.
3D volumes of neurons.
Convolutional Neural Networks take advantage of the fact that the input consists of images and they constrain the architecture in a more sensible way.
In particular, unlike a regular Neural Network, the layers of a ConvNet have neurons arranged in 3 dimensions: width, height, depth. (Note that the word depth here refers to the third dimension of an activation volume, not to the depth of a full Neural Network, which can refer to the total number of layers in a network.)
For example, the input images in CIFAR-10 are an input volume of activations, and the volume has dimensions 32x32x3 (width, height, depth respectively).
As we will soon see, the neurons in a layer will only be connected to a small region of the layer before it, instead of all of the neurons in a fully-connected manner.
Moreover, the final output layer would for CIFAR-10 have dimensions 1x1x10, because by the end of the ConvNet architecture we will reduce the full image into a single vector of class scores, arranged along the depth dimension. Here is a visualization:
- 뉴런의 3D 볼륨.
- CNN은 입력을 이미지로 받을 수 있고 이미지를 합리적인 방식에 아키텍처로 구성할 수 있는 장점이 있다.
- 특히 일반적인 뉴런 네트워크랑 달리 CNN은 3차원 Width, height, depth 를 가지고 있다. (Depth 단어는 activation volume의 깊이을 의미하며 전체 신경망의 깊이가 아니라 네트워크 총 레이어 수를 의미한다.)
- 예를 들어 CIFAR-10 depth 입력 이미지는 Activation의 입력 볼륨이고 볼륨에 차원은 32 * 32 * 3이다 (width, height, depth).
- 곧 알게 되겠지만, 레이어의 뉴런은 완전히 연결된 방식으로 모든 뉴런이 연결되는 대신 이전 레이어의 작은 영역에만 연결된다.
- ConvNet 아키텍쳐는 전체 이미지를 클래스 점수들로 이뤄진 하나의 벡터로 만들어주기 때문에 마지막 출력 레이어는 1x1x10(10은 CIFAR-10 데이터의 클래스 개수)의 차원을 가지게 된다. 이에 대한 그럼은 아래와 같다.
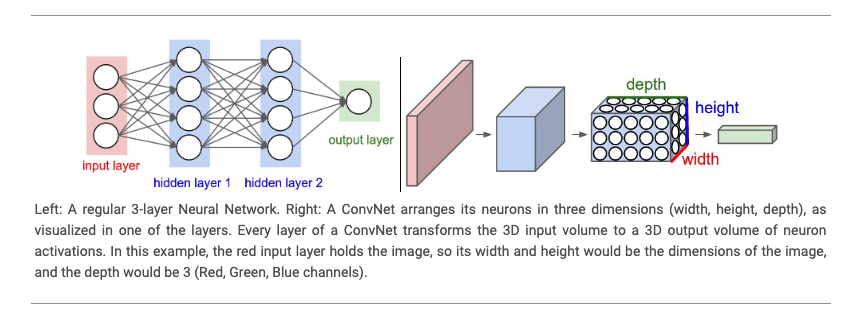
Left: A regular 3-layer Neural Network. Right: A ConvNet arranges its neurons in three dimensions (width, height, depth), as visualized in one of the layers.
Every layer of a ConvNet transforms the 3D input volume to a 3D output volume of neuron activations.
In this example, the red input layer holds the image, so its width and height would be the dimensions of the image, and the depth would be 3 (Red, Green, Blue channels).
- 왼쪽: 일반적인 3층 신경망입니다. 오른쪽: ConvNet은 뉴런을 3차원(폭, 높이, 깊이)으로 배열합니다. 레이어 중 하나에서 시각화됩니다.
- ConvNet의 모든 레이어는 3D 입력 볼륨을 뉴런 활성화의 3D 출력 볼륨으로 변환합니다.
- 이 예에서 빨간색 입력 레이어는 이미지를 고정하므로 입력 레이어의 너비와 높이는 이미지의 치수가 되고 깊이는 3(빨간색, 녹색, 파란색 채널)이 됩니다.
A ConvNet is made up of Layers. Every Layer has a simple API: It transforms an input 3D volume to an output 3D volume with some differentiable function that may or may not have parameters.
- ConvNet은 레이어로 구성됩니다. 모든 레이어에는 간단한 API가 있습니다.
- 매개변수가 있거나 없을 수 있는 차별화 가능한 기능을 사용하여 입력 3D 볼륨을 출력 3D 볼륨으로 변환합니다.
2 Layers used to build ConvNets
As we described above, a simple ConvNet is a sequence of layers, and every layer of a ConvNet transforms one volume of activations to another through a differentiable function.
We use three main types of layers to build ConvNet architectures: Convolutional Layer, Pooling Layer, and Fully-Connected Layer (exactly as seen in regular Neural Networks).
We will stack these layers to form a full ConvNet architecture.
- 위에서 다룬 것과 같이, ConvNet의 각 레이어는 미분 가능한 변환 함수를 통해 하나의 액티베이션 볼륨을 또다른 액티베이션 볼륨으로 변환 (transform) 시킨다.
- ConvNet 아키텍쳐에서는 크게 컨볼루셔널 레이어, 풀링 레이어, Fully-connected 레이어라는 3개 종류의 레이어가 사용된다.
- 전체 ConvNet 아키텍쳐는 이 3 종류의 레이어들을 쌓아 만들어진다.
Example Architecture: Overview.
We will go into more details below, but a simple ConvNet for CIFAR-10 classification could have the architecture [INPUT - CONV - RELU - POOL - FC]. In more detail:
- 예제: 아래에서 더 자세하게 배우겠지만, CIFAR-10 데이터를 다루기 위한 간단한 ConvNet은 [INPUT - CONV - RELU - POOL - FC]로 구축할 수 있다.
INPUT [32x32x3] will hold the raw pixel values of the image, in this case an image of width 32, height 32, and with three color channels R,G,B.
- INPUT 입력 이미지가 가로32, 세로32, 그리고 RGB 채널을 가지는 경우 입력의 크기는 [32x32x3].
CONV layer will compute the output of neurons that are connected to local regions in the input, each computing a dot product between their weights and a small region they are connected to in the input volume.
This may result in volume such as [32x32x12] if we decided to use 12 filters.
- CONV 레이어는 입력의 로컬 영역에 연결된 뉴런의 출력을 계산하며, 각 뉴런은 가중치와 입력 크기에서 연결된 작은 영역 사이의 내적을 계산합니다.
- 12개의 필터를 사용하기로 결정한 경우 [32x32x12]와 같은 볼륨이 발생할 수 있습니다.
RELU layer will apply an elementwise activation function, such as the \(max(0,x)\) thresholding at zero.
This leaves the size of the volume unchanged ([32x32x12]).
- RELU 레이어는 max(0,x)와 같은 요소별 활성화 함수를 적용합니다. 제로 임계값.
- 이렇게 하면 차원 크기가 변경되지 않습니다([32x32x12]).
POOL layer will perform a downsampling operation along the spatial dimensions (width, height), resulting in volume such as [16x16x12].
- POOL 레이어는 공간 차원(너비, 높이)에 따라 다운샘플링 작업을 수행하여 [16x16x12]와 같은 차원을 생성합니다.
FC (i.e. fully-connected) layer will compute the class scores, resulting in volume of size [1x1x10], where each of the 10 numbers correspond to a class score, such as among the 10 categories of CIFAR-10.
As with ordinary Neural Networks and as the name implies, each neuron in this layer will be connected to all the numbers in the previous volume.
- FC(즉, 완전 연결) 계층은 클래스 점수를 계산하여 [1x1x10] 크기의 차원을 생성합니다. 여기서 10개의 각 숫자는 CIFAR-10의 10개 범주 중에서 클래스 점수에 해당합니다.
- 일반 신경망과 마찬가지로 이름에서 알 수 있듯이 이 계층의 각 뉴런은 이전 차원의 모든 숫자에 연결됩니다.
In this way, ConvNets transform the original image layer by layer from the original pixel values to the final class scores.
Note that some layers contain parameters and other don’t.
In particular, the CONV/FC layers perform transformations that are a function of not only the activations in the input volume, but also of the parameters (the weights and biases of the neurons).
On the other hand, the RELU/POOL layers will implement a fixed function.
The parameters in the CONV/FC layers will be trained with gradient descent so that the class scores that the ConvNet computes are consistent with the labels in the training set for each image.
- 이러한 방식으로 ConvNets는 원본 이미지 레이어를 원본 픽셀 값에서 최종 클래스 점수로 변환합니다.
- 일부 레이어에는 매개변수가 포함되어 있고 다른 레이어에는 포함되어 있지 않습니다.
- 특히 CONV/FC 레이어는 입력 볼륨의 활성화뿐만 아니라 매개변수(뉴런의 가중치 및 편향)의 함수인 변환을 수행합니다.
- 반면에 RELU/POOL 계층은 고정 기능을 구현합니다.
- CONV/FC 레이어의 매개변수는 ConvNet이 계산하는 클래스 점수가 각 이미지에 대한 훈련 세트의 레이블과 일치하도록 경사 하강법으로 훈련됩니다.
In summary: A ConvNet architecture is in the simplest case a list of Layers that transform the image volume into an output volume (e.g. holding the class scores)
- ConvNet 아키텍쳐는 여러 레이어를 통해 입력 이미지 크기을 출력 볼륨 ( 클래스 점수 )으로 변환시켜 준다.
There are a few distinct types of Layers (e.g. CONV/FC/RELU/POOL are by far the most popular)
- ConvNet은 몇 가지 종류의 레이어로 구성되어 있다. CONV/FC/RELU/POOL 레이어가 현재 가장 많이 쓰인다.
Each Layer accepts an input 3D volume and transforms it to an output 3D volume through a differentiable function
- 각 레이어는 3차원의 입력 크기을 미분 가능한 함수를 통해 3차원 출력 크기로 변환시킨다.
Each Layer may or may not have parameters (e.g. CONV/FC do, RELU/POOL don’t)
- parameter가 있는 레이어도 있고 그렇지 않은 레이어도 있다 (FC/CONV는 모수를 갖고 있고, RELU/POOL 등은 모수가 없음).
Each Layer may or may not have additional hyperparameters (e.g. CONV/FC/POOL do, RELU doesn’t)
- hyperparameter가 있는 레이어도 있고 그렇지 않은 레이어도 있다 (CONV/FC/POOL 레이어는 초모수를 가지며 RELU는 가지지 않음).
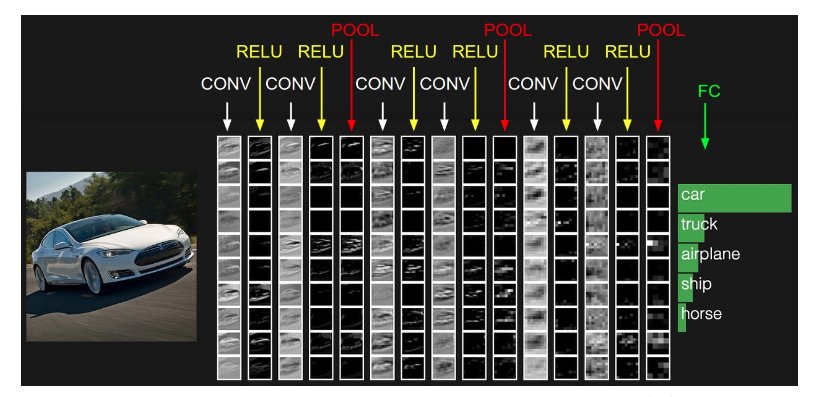
The activations of an example ConvNet architecture.
The initial volume stores the raw image pixels (left) and the last volume stores the class scores (right).
Each volume of activations along the processing path is shown as a column.
Since it’s difficult to visualize 3D volumes, we lay out each volume’s slices in rows.
The last layer volume holds the scores for each class, but here we only visualize the sorted top 5 scores, and print the labels of each one.
The full web-based demo is shown in the header of our website.
The architecture shown here is a tiny VGG Net, which we will discuss later.
- ConvNet 아키텍쳐의 액티베이션 (activation) 예제.
- 첫 볼륨은 로우 이미지(raw image)를 다루며, 마지막 볼륨은 클래스 점수들을 출력한다.
- 입/출력 사이의 액티베이션들은 그림의 각 열에 나타나 있다.
- 3차원 볼륨을 시각적으로 나타내기가 어렵기 때문에 각 행마다 볼륨들의 일부만 나타냈다.
- 마지막 레이어는 모든 클래스에 대한 점수를 나타내지만 여기에서는 상위 5개 클래스에 대한 점수와 레이블만 표시했다.
- 전체 웹데모는 우리의 웹사이트 상단에 있다.
- 여기에서 사용된 아키텍쳐는 작은 VGG Net이다.
We now describe the individual layers and the details of their hyperparameters and their connectivities.
- 이제 각각의 레이어에 대해 hyperparameter, connectivity 등의 세부 사항들을 알아보도록 하자.
2.1 Convolution Layer
The Conv layer is the core building block of a Convolutional Network that does most of the computational heavy lifting.
- Conv 계층은 대부분의 복잡한 컴퓨팅 작업을 수행하는 Convolutional Network의 핵심 빌딩 블록입니다.
Overview and intuition without brain stuff.
Let’s first discuss what the CONV layer computes without brain/neuron analogies.
The CONV layer’s parameters consist of a set of learnable filters.
Every filter is small spatially (along width and height), but extends through the full depth of the input volume.
For example, a typical filter on a first layer of a ConvNet might have size 5x5x3 (i.e. 5 pixels width and height, and 3 because images have depth 3, the color channels).
During the forward pass, we slide (more precisely, convolve) each filter across the width and height of the input volume and compute dot products between the entries of the filter and the input at any position.
As we slide the filter over the width and height of the input volume we will produce a 2-dimensional activation map that gives the responses of that filter at every spatial position.
Intuitively, the network will learn filters that activate when they see some type of visual feature such as an edge of some orientation or a blotch of some color on the first layer, or eventually entire honeycomb or wheel-like patterns on higher layers of the network. Now, we will have an entire set of filters in each CONV layer (e.g. 12 filters), and each of them will produce a separate 2-dimensional activation map.
We will stack these activation maps along the depth dimension and produce the output volume.
(input volume 입력 크기)
- 리뷰 그리고 감각적인 직관.
- CONV Layer 첫번째 논의는 생각/Neuron 유추없이 계산하는 것이다.
- Conv layer의 파라미터는 학습 가능한 필터로 구성되어 있다.
- 모든 공간적으로 작다(3 by 3, 7 by 7 의미)(width, height 속해있음), 그러나 입력 크기의 깊이에 따라 확장한다.
- ConvNet의 첫번째 일반적인 필터는 5x5x3 크기(width : 5, height : 5, depth: 3)를 가지고 있다.
- Forward pass 하는 동안에는, 입력데이터들을 상하 좌우로 움직이고, 필터안에 있는 값과 입력 데이터안에 위치한 값을 내적 계산한다.
- 필터를 입력 데이터에 상하 좌우로 움직일 때, 우리는 모든 공간을 돌아다닌 2차원 activation map 얻을 것이다.
- 직관적으로, 네트워크는 첫 번째 레이어에서 일부 방향의 가장자리 또는 일부 색상의 얼룩, 또는 궁극적으로 네트워크의 상위 레이어에서 전체 벌집 또는 바퀴 모양의 패턴과 같은 시각적 기능 유형을 볼 때 활성화되는 필터를 학습합니다.
Now, we will have an entire set of filters in each CONV layer (e.g. 12 filters), and each of them will produce a separate 2-dimensional activation map.
We will stack these activation maps along the depth dimension and produce the output volume.
- 이제 각 CONV 레이어에 전체 필터 세트(예: 12개 필터)가 있고 각 필터는 별도의 2차원 활성화 맵을 생성합니다.
- 이러한 활성화 맵을 깊이 차원을 따라 쌓고 출력 볼륨을 생성합니다.
The brain view. If you’re a fan of the brain/neuron analogies, every entry in the 3D output volume can also be interpreted as an output of a neuron that looks at only a small region in the input and shares parameters with all neurons to the left and right spatially (since these numbers all result from applying the same filter).
- 3D 출력 볼륨의 모든 항목은 입력의 작은 영역만 보고 공간적으로 왼쪽과 오른쪽에 있는 모든 뉴런과 매개변수를 공유하는 뉴런의 출력으로 해석될 수 있습니다(이 숫자는 모두 동일한 필터를 적용한 결과이기 때문입니다).
We now discuss the details of the neuron connectivities, their arrangement in space, and their parameter sharing scheme.
- 이제 뉴런 연결, 공간에서의 배열 및 매개 변수 공유 체계에 대해 자세히 설명합니다.
Local Connectivity. When dealing with high-dimensional inputs such as images, as we saw above it is impractical to connect neurons to all neurons in the previous volume. Instead, we will connect each neuron to only a local region of the input volume. The spatial extent of this connectivity is a hyperparameter called the receptive field of the neuron (equivalently this is the filter size). The extent of the connectivity along the depth axis is always equal to the depth of the input volume. It is important to emphasize again this asymmetry in how we treat the spatial dimensions (width and height) and the depth dimension: The connections are local in 2D space (along width and height), but always full along the entire depth of the input volume.
- 이미지와 같은 고차원 입력을 다룰 때에는, 현재 레이어의 한 뉴런을 이전 볼륨의 모든 뉴런들과 연결하는 것이 비 실용적이다.
- 대신에 우리는 레이어의 각 뉴런을 입력 볼륨의 로컬한 영역(local region)에만 연결할 것이다.
- 이 영역은 리셉티브 필드 (receptive field = filter)라고 불리는 hyperparameter 이다.
- 깊이 차원 측면에서는 항상 입력 볼륨의 총 깊이를 다룬다 (가로/세로는 작은 영역을 보지만 깊이는 전체를 본다는 뜻).
- 공간적 차원 (가로/세로)와 깊이 차원을 다루는 방식이 다르다는 걸 기억하자.
Example 1.
For example, suppose that the input volume has size [32x32x3], (e.g. an RGB CIFAR-10 image).
If the receptive field (or the filter size) is 5x5, then each neuron in the Conv Layer will have weights to a [5x5x3] region in the input volume, for a total of 5*5*3 = 75 weights (and +1 bias parameter).
Notice that the extent of the connectivity along the depth axis must be 3, since this is the depth of the input volume.
- 예 1. 예를 들어, 입력 볼륨의 크기가 [32x32x3]이라고 가정합니다(예: RGB CIFAR-10 영상).
- 영역(receptive field) 필드(또는 필터 크기)가 5x5이면 Conv Layer의 각 뉴런은 입력 볼륨에서 [5x5x3] 영역에 대한 가중치를 가지며, 총 5*5*3 = 75 가중치(및 +1 바이어스 파라미터)입니다.
- 깊이 축을 따라 연결되는 범위는 입력 볼륨의 깊이이므로 3이어야 합니다.
Example 2.
Suppose an input volume had size [16x16x20].
Then using an example receptive field size of 3x3, every neuron in the Conv Layer would now have a total of 3*3*20 = 180 connections to the input volume.
Notice that, again, the connectivity is local in 2D space (e.g. 3x3), but full along the input depth (20).
- 예 2.
- 입력 볼륨의 크기가 [16x16x20]이라고 가정합니다.
- 그런 다음 3x3의 수신 필드 크기의 예를 사용하여 Conv Layer의 모든 뉴런은 이제 입력 볼륨에 대한 총 3*3*20 = 180개의 연결을 가질 것입니다.
- 2D 공간(예: 3x3)에서는 연결이 로컬이지만 입력 깊이(20)를 따라 가득 찬다는 점에 유의하십시오.
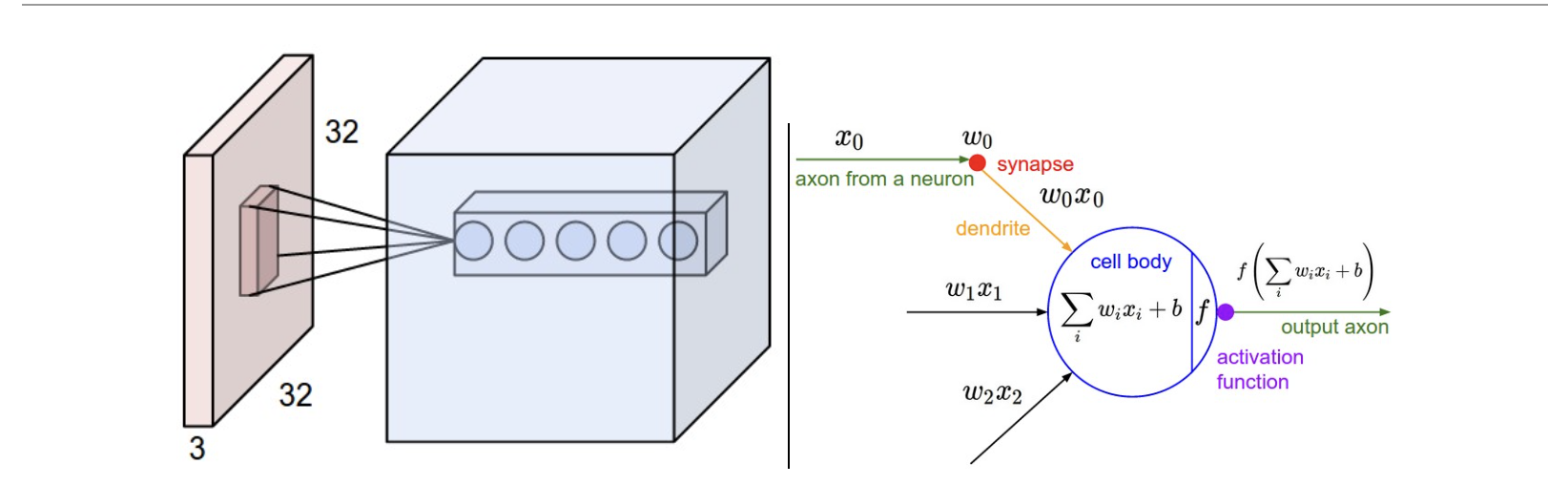
Left
An example input volume in red (e.g. a 32x32x3 CIFAR-10 image), and an example volume of neurons in the first Convolutional layer.
Each neuron in the convolutional layer is connected only to a local region in the input volume spatially, but to the full depth (i.e. all color channels).
Note, there are multiple neurons (5 in this example) along the depth, all looking at the same region in the input:
the lines that connect this column of 5 neurons do not represent the weights (i.e. these 5 neurons do not share the same weights, but they are associated with 5 different filters), they just indicate that these neurons are connected to or looking at the same receptive field or region of the input volume, i.e. they share the same receptive field but not the same weights.
- 입력 사이즈는 32 * 32* 3 그리고 첫 번째 뉴런 볼륨은 컨볼루션 Layer 이다.
- Conv layer 각각에 뉴런은 입력 사이즈 공간안에 로컬영역으로 연결되어 있지만, 입력 사이즈에 depth(모든 색상 채널) 연결된다.
- 여러개의 깊이에 따라 뉴런(예시 5개)이 있으며, 모두 입력에서 동일한 영역을 보고있다. 5개의 뉴런의 컬럼은 연결하는 선은 가중치를 나타나지 않는다. (5개의 뉴런은 가중치를 공유하지 않는다, 그러나 필터는 관련이 있다.)
- 5개의 뉴런은 단지 뉴런이 입력 볼륨의 Receptive filed 또는 input영역에 연결되어 있거나 보고 있음을 나타내고 있다. 5개의 뉴런들은 즉 동일한 Receptive filed 공유하지 가중치는 공유하지 않는다.
- 가중치를 공유하는 것이 아니라 filter를 통해 가중치를 업데이트 한다.
Right The neurons from the Neural Network chapter remain unchanged: They still compute a dot product of their weights with the input followed by a non-linearity, but their connectivity is now restricted to be local spatially.
- 이전에 배웠던 신명망 CH 배웠던 Neurons 변경없이 유지되고 있다.
- 그들인 여전히 가중치를 내적하여 계산한다.
- 입력에 이어 비선형성이 있는 가중치의 내적을 여저히 계산하지만 이제 연결이 공간적으로 로컬로 제한됩니다.
Spatial arrangement.
We have explained the connectivity of each neuron in the Conv Layer to the input volume, but we haven’t yet discussed how many neurons there are in the output volume or how they are arranged.
Three hyperparameters control the size of the output volume: the depth, stride and zero-padding. We discuss these next:
- 공간적 배열
- 입력 볼륨과 Conv layer 각각에 뉴런에 입력되는 것을 설명을 했다. 그러나 우리는 어떻게 Output 뉴런이 몇개인지, 배열되어 있는지 논의하지 않았다.
- 3개의 하이퍼파라미터는 Output 사이즈에 대해 제한하게 된다. (깊이, 보폭 및 제로 패딩 에대해 이야기할것)
‘First, the depth of the output volume is a hyperparameter: it corresponds to the number of filters we would like to use, each learning to look for something different in the input.
For example, if the first Convolutional Layer takes as input the raw image, then different neurons along the depth dimension may activate in presence of various oriented edges, or blobs of color.
We will refer to a set of neurons that are all looking at the same region of the input as a depth column (some people also prefer the term fibre).
- 첫번째 Output 사이즈 하이퍼파리미터 설정 그것은 우리가 사용하고 싶은 필터의 수에 해당한다, 각각은 입력안에 다른 것들을 찾아 학습할 것이다.
- 예를 들어 만약 Conv Layer는 raw image를 가지고 있을 때, 다른 뉴런들은 차원 depth 따라 다양한 방향의 가장자리 또는 색상에 특징이 있을 때 활성화 할 수 있다.
- 우리는 입력 depth 안에 있는 같은 영역을 보고 있는 뉴런들에 배치를 선호할 것이다.(일부 사람들은 fibre 용어를 선호하기도 한다.)
Second, we must specify the stride with which we slide the filter.
When the stride is 1 then we move the filters one pixel at a time.
When the stride is 2 (or uncommonly 3 or more, though this is rare in practice) then the filters jump 2 pixels at a time as we slide them around. This will produce smaller output volumes spatially.
-
두 번째 슬라이드 하는 포폭을 결정해야한다.
- 보폭이 1이면 필터를 한번에 학 픽셀씩 이동한다.
- 보폭이 2면(실제로는 거의 없지만 일반적이지 않은 3 이상)인 경우 필터를 슬라이드 할 때 필터가 한번에 2 픽셀씩 움직인다.
- 이렇게 공간적으로 더 작은 출력 볼륨이 생성된다.
As we will soon see, sometimes it will be convenient to pad the input volume with zeros around the border. The size of this zero-padding is a hyperparameter. The nice feature of zero padding is that it will allow us to control the spatial size of the output volumes (most commonly as we’ll see soon we will use it to exactly preserve the spatial size of the input volume so the input and output width and height are the same).
- 곧 알게 되겠지만 때로는 입력 볼륨을 테두리 주위에 0으로 채우는 것이 편리할 것입니다.
- 이 제로 패딩의 크기는 하이퍼파라미터입니다.
- 제로 패딩의 좋은 기능은 출력 볼륨의 공간 크기를 제어할 수 있다는 것입니다. 높이가 동일합니다.)
We can compute the spatial size of the output volume as a function of the input volume size (\(W\)), the receptive field size of the Conv Layer neurons (\(F\)), the stride with which they are applied (\(S\)), and the amount of zero padding used (\(P\)) on the border. You can convince yourself that the correct formula for calculating how many neurons “fit” is given by \((W - F + 2P)/S + 1\). For example for a 7x7 input and a 3x3 filter with stride 1 and pad 0 we would get a 5x5 output. With stride 2 we would get a 3x3 output. Lets also see one more graphical example:
- 출력 볼륨의 공간 크기는 입력 볼륨 크기(\(W\)), Conv Layer 뉴런의 수용 필드 크기(\(F\)), 적용되는 보폭(\(S\)), 테두리에 사용된 제로 패딩(\(P\)).
- 얼마나 많은 뉴런이 “맞는지”를 계산하는 올바른 공식이 \((W - F + 2P)/S + 1\) 이라는 것을 스스로 확신할 수 있습니다. 예를 들어 7x7 입력과 stride 1 및 pad 0이 있는 3x3 필터의 경우 5x5 출력을 얻습니다. 보폭이 2이면 3x3 출력이 됩니다.
- 그래픽 예제를 하나 더 살펴보겠습니다.
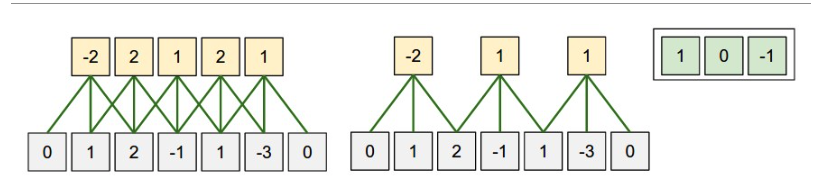
Illustration of spatial arrangement.
In this example there is only one spatial dimension (x-axis), one neuron with a receptive field size of F = 3, the input size is W = 5, and there is zero padding of P = 1.
Left: The neuron strided across the input in stride of S = 1, giving output of size (5 - 3 + 2)/1+1 = 5.
Right: The neuron uses stride of S = 2, giving output of size (5 - 3 + 2)/2+1 = 3. Notice that stride S = 3 could not be used since it wouldn’t fit neatly across the volume. In terms of the equation, this can be determined since (5 - 3 + 2) = 4 is not divisible by 3.
- 공간 배열의 그림입니다.
- 이 예에는 하나의 공간 차원(x축), receptive field 크기가 F = 3인 뉴런 하나, 입력 크기는 W = 5, P = 1의 제로 패딩이 있습니다.
- 왼쪽: 스트라이드된 뉴런 S = 1의 보폭으로 입력에 걸쳐 크기 (5 - 3 + 2)/1+1 = 5의 출력을 제공합니다.
- 오른쪽: 뉴런은 S = 2의 보폭을 사용하여 크기 (5 - 3 + 2)의 출력을 제공합니다. /2+1 = 3. stride S = 3은 볼륨 전체에 깔끔하게 맞지 않기 때문에 사용할 수 없습니다. 방정식의 관점에서 이것은 (5 - 3 + 2) = 4가 3으로 나누어지지 않기 때문에 결정될 수 있습니다.
The neuron weights are in this example [1,0,-1] (shown on very right), and its bias is zero. These weights are shared across all yellow neurons (see parameter sharing below).
- 뉴런 가중치는 이 예에서 [1,0,-1](맨 오른쪽에 표시됨)이고 바이어스는 0입니다. 이러한 가중치는 모든 노란색 뉴런에서 공유됩니다(아래 매개변수 공유 참조).
Use of zero-padding.
In the example above on left, note that the input dimension was 5 and the output dimension was equal: also 5.
This worked out so because our receptive fields were 3 and we used zero padding of 1.
If there was no zero-padding used, then the output volume would have had spatial dimension of only 3, because that is how many neurons would have “fit” across the original input.
In general, setting zero padding to be \(P = (F - 1)/2\) when the stride is \(S = 1\) ensures that the input volume and output volume will have the same size spatially.
It is very common to use zero-padding in this way and we will discuss the full reasons when we talk more about ConvNet architectures.
- 제로 패딩 사용.
- 위의 왼쪽 예에서 입력 차원이 5이고 출력 차원도 5라는 점에 유의하십시오.
- 이는 수용 필드가 3이고 제로 패딩을 1로 사용했기 때문에 가능했습니다. 제로 패딩이 사용되지 않은 경우 , 그러면 출력 볼륨의 공간 차원은 3이 됩니다.
- 원래 입력에 "맞는" 뉴런의 수이기 때문입니다.
- 일반적으로 스트라이드가 \(S = 1\)일 때 제로 패딩을 \(P = (F - 1)/2\)로 설정하면 입력 볼륨과 출력 볼륨이 공간적으로 동일한 크기를 갖게 됩니다.
- 이러한 방식으로 제로 패딩을 사용하는 것은 매우 일반적이며 ConvNet 아키텍처에 대해 자세히 이야기할 때 전체 이유를 논의할 것입니다.
Constraints on strides.
Note again that the spatial arrangement hyperparameters have mutual constraints.
For example, when the input has size \(W = 10\), no zero-padding is used \(P = 0\), and the filter size is \(F = 3\), then it would be impossible to use stride \(S = 2\), since \((W - F + 2P)/S + 1 = (10 - 3 + 0) / 2 + 1 = 4.5\), i.e. not an integer, indicating that the neurons don’t “fit” neatly and symmetrically across the input.
Therefore, this setting of the hyperparameters is considered to be invalid, and a ConvNet library could throw an exception or zero pad the rest to make it fit, or crop the input to make it fit, or something.
As we will see in the ConvNet architectures section, sizing the ConvNets appropriately so that all the dimensions “work out” can be a real headache, which the use of zero-padding and some design guidelines will significantly alleviate.
- 보폭에 대한 제약.
- 공간 배열 하이퍼 파라미터에는 상호 제약이 있습니다.
- 예를 들어, 입력의 크기가 \(W = 10\)이고, 패딩 \(P = 0\), 필터 사이즈 \(F = 3\) 사용할 때, \((W - F + 2P)/S + 1 = (10 - 3 + 0) / 2 + 1 = 4.5\)이므로 스트라이드 S=2를 사용하는 것은 불가능할 것입니다.
- 즉, 뉴런이 입력에 "정렬하게 맞지 않고" 대칭적으로 맞지 않음을 나타냅니다.
- 따라서 이 하이퍼 파라미터 설정은 유효하지 않은 것으로 간주되며, ConvNet 라이브러리는 예외를 던지거나 나머지 패드를 0으로 만들어 적합하게 만들거나 입력을 잘라 적합하게 만들 수 있습니다.
- ConvNet 아키텍처 섹션에서 볼 수 있듯이, 모든 차원이 "해결"될 수 있도록 ConvNet의 크기를 적절하게 조정하는 것은 제로 패딩과 일부 설계 지침의 사용을 크게 완화시킬 것입니다.
Real-world example.
The Krizhevsky et al. architecture that won the ImageNet challenge in 2012 accepted images of size [227x227x3].
On the first Convolutional Layer, it used neurons with receptive field size \(F = 11\), stride \(S = 4\) and no zero padding \(P = 0\).
Since (227 - 11)/4 + 1 = 55, and since the Conv layer had a depth of \(K = 96\), the Conv layer output volume had size [55x55x96].
Each of the 55*55*96 neurons in this volume was connected to a region of size [11x11x3] in the input volume.
Moreover, all 96 neurons in each depth column are connected to the same [11x11x3] region of the input, but of course with different weights.
As a fun aside, if you read the actual paper it claims that the input images were 224x224, which is surely incorrect because (224 - 11)/4 + 1 is quite clearly not an integer.
This has confused many people in the history of ConvNets and little is known about what happened.
My own best guess is that Alex used zero-padding of 3 extra pixels that he does not mention in the paper.
- 실제 사례.
- Krizhevsky et al. 2012년 ImageNet Challenge에서 우승한 아키텍처는 [227x227x3] 크기의 이미지를 허용했습니다.
- 첫 번째 컨볼루션 레이어에서는 수용 필드 크기 \(F = 11\), 보폭 \(S = 11\), 제로 패딩 없음 \(P = 11\)인 뉴런을 사용했습니다.
- (227 - 11)/4 + 1 = 55이고 Conv 레이어의 깊이가 \(K = 96\) 이므로 Conv 레이어 출력 볼륨의 크기는 [55x55x96]입니다.
- 이 볼륨의 55*55*96개 뉴런 각각은 입력 볼륨의 [11x11x3] 크기 영역에 연결되었습니다.
- 또한 각 깊이 열의 모든 96개 뉴런은 입력의 동일한 [11x11x3] 영역에 연결되지만 물론 가중치는 다릅니다.
- 재미는 제쳐두고 실제 논문을 읽으면 입력 이미지가 224x224라고 주장합니다.
- (224 - 11)/4 + 1은 분명히 정수가 아니기 때문에 확실히 잘못된 것입니다.
- 이것은 ConvNets의 역사에서 많은 사람들을 혼란스럽게 했으며 무슨 일이 일어났는지에 대해서는 알려진 바가 거의 없습니다.
- 내 자신의 최선의 추측은 Alex가 논문에서 언급하지 않은 3개의 추가 픽셀의 제로 패딩을 사용했다는 것입니다.
Parameter Sharing. Parameter sharing scheme is used in Convolutional Layers to control the number of parameters. Using the real-world example above, we see that there are 55*55*96 = 290,400 neurons in the first Conv Layer, and each has 11*11*3 = 363 weights and 1 bias. Together, this adds up to 290400 * 364 = 105,705,600 parameters on the first layer of the ConvNet alone. Clearly, this number is very high.
- 매개변수 공유.
- 매개변수 공유 방식은 Convolutional Layers에서 매개변수 수를 제어하는 데 사용됩니다. 위의 실제 예를 사용하면 첫 번째 Conv Layer에 55*55*96 = 290,400개의 뉴런이 있고 각각 11*11*3 = 363개의 가중치와 1개의 바이어스가 있음을 알 수 있습니다.
- 이를 합치면 ConvNet의 첫 번째 레이어에만 최대 290400 * 364 = 105,705,600 개의 매개변수가 추가됩니다. 분명히 이 숫자는 매우 높습니다.
It turns out that we can dramatically reduce the number of parameters by making one reasonable assumption:
That if one feature is useful to compute at some spatial position (x,y), then it should also be useful to compute at a different position (x2,y2).
In other words, denoting a single 2-dimensional slice of depth as a depth slice (e.g. a volume of size [55x55x96] has 96 depth slices, each of size [55x55]), we are going to constrain the neurons in each depth slice to use the same weights and bias.
With this parameter sharing scheme, the first Conv Layer in our example would now have only 96 unique set of weights (one for each depth slice), for a total of 96*11*11*3 = 34,848 unique weights, or 34,944 parameters (+96 biases).
Alternatively, all 55*55 neurons in each depth slice will now be using the same parameters.
In practice during backpropagation, every neuron in the volume will compute the gradient for its weights, but these gradients will be added up across each depth slice and only update a single set of weights per slice.
- 다음과 같은 한 가지 합리적인 가정을 통해 매개변수의 수를 크게 줄일 수 있습니다:
- 어떤 공간 위치(x,y)에서 하나의 형상이 계산하는 데 유용하다면 다른 위치(x2,y2)에서도 계산하는 것이 유용해야 합니다.
- 즉, 깊이의 단일 2차원 슬라이스를 깊이 슬라이스로 표시(예: 크기 [55x55x96] 볼륨에는 96개의 깊이 슬라이스가 있으며 각 크기 [55x55]), 각 깊이 슬라이스의 뉴런이 동일한 가중치와 편향을 사용하도록 제한합니다.
- 이 매개 변수 공유 체계를 사용하면 이 예제의 첫 번째 Conv 레이어는 이제 96개의 고유 가중치 집합(각 깊이 슬라이스에 대해 하나씩)만 가질 것이며, 총 96*11*11*3 = 34,848개의 고유 가중치 또는 34,944개의 매개 변수(+96 바이어스)에 대해 사용됩니다.
- 또는 각 깊이 슬라이스의 모든 55*55 뉴런이 이제 동일한 매개 변수를 사용합니다.
- 실제로 역전파 중에 볼륨의 모든 뉴런은 가중치에 대한 기울기를 계산하지만 이러한 기울기는 각 깊이 슬라이스에 걸쳐 합산되고 슬라이스당 단일 가중치 세트만 업데이트됩니다.
Notice that if all neurons in a single depth slice are using the same weight vector, then the forward pass of the CONV layer can in each depth slice be computed as a convolution of the neuron’s weights with the input volume (Hence the name: Convolutional Layer).
This is why it is common to refer to the sets of weights as a filter (or a kernel), that is convolved with the input.
- 단일 깊이 슬라이스의 모든 뉴런이 동일한 가중치 벡터를 사용하는 경우 각 깊이 슬라이스에서 CONV 레이어의 순방향 패스는 뉴런 가중치와 입력 볼륨의 합성곱으로 계산될 수 있습니다(따라서 이름: Convolutional Layer ).
- 이것이 가중치 집합을 입력과 컨볼루션되는 필터(또는 커널)로 참조하는 것이 일반적인 이유입니다.

Example filters learned by Krizhevsky et al. Each of the 96 filters shown here is of size [11x11x3], and each one is shared by the 5555 neurons in one depth slice.
Notice that the parameter sharing assumption is relatively reasonable: If detecting a horizontal edge is important at some location in the image, it should intuitively be useful at some other location as well due to the translationally-invariant structure of images.
There is therefore no need to relearn to detect a horizontal edge at every one of the 5555 distinct locations in the Conv layer output volume.
- Krizhevsky 등이 학습한 예제 필터. 여기에 표시된 96개의 필터는 각각 [11x11x3] 크기이며 각 필터는 하나의 깊이 슬라이스에서 55*55 뉴런에 의해 공유됩니다.
- 매개변수 공유 가정은 상대적으로 타당합니다. 이미지의 일부 위치에서 수평 가장자리 감지가 중요한 경우 이미지의 변환 불변 구조로 인해 다른 위치에서도 직관적으로 유용해야 합니다.
- 따라서 Conv 레이어 출력 볼륨의 55*55 개별 위치에서 수평 에지를 감지하기 위해 다시 학습할 필요가 없습니다.
Note that sometimes the parameter sharing assumption may not make sense.
This is especially the case when the input images to a ConvNet have some specific centered structure, where we should expect,
for example, that completely different features should be learned on one side of the image than another.
One practical example is when the input are faces that have been centered in the image. You might expect that different eye-specific or hair-specific features could (and should) be learned in different spatial locations.
In that case it is common to relax the parameter sharing scheme, and instead simply call the layer a Locally-Connected Layer.
- 때로는 매개변수 공유 가정이 이해가 되지 않을 수도 있습니다.
- 이것은 특히 ConvNet에 대한 입력 이미지가 특정 중심 구조를 가지고 있는 경우입니다.
- 예를 들어 이미지의 한쪽에서 다른 쪽과 완전히 다른 기능을 학습해야 합니다.
- 하나의 실질적인 예는 입력이 이미지의 중앙에 있는 얼굴인 경우입니다.
- 다른 눈 특정 또는 머리카락 특정 기능이 다른 공간 위치에서 학습될 수 있고 학습되어야 한다고 예상할 수 있습니다.
- 이 경우 매개변수 공유 체계를 완화하고 대신 단순히 로컬 연결 계층이라고 부르는 것이 일반적입니다.
Numpy examples. To make the discussion above more concrete, lets express the same ideas but in code and with a specific example. Suppose that the input volume is a numpy array X. Then:
- numpy 예제.
- 위의 논의를 보다 구체적으로 만들기 위해 동일한 아이디어를 코드와 구체적인 예를 통해 표현해 보겠습니다. 입력 볼륨이 numpy 배열 X라고 가정합니다. 그런 다음:
A depth column (or a fibre) at position (x,y) would be the activations X[x,y,:].
A depth slice, or equivalently an activation map at depth d would be the activations X[:,:,d].
-
위치 (x,y)의 깊이 열(또는 섬유)은 활성화 X[x,y,:]입니다.
-
깊이 슬라이스 또는 깊이 d에서의 활성화 맵은 활성화 X[:,:,d]가 됩니다.
Conv Layer Example. Suppose that the input volume X has shape X.shape: (11,11,4). Suppose further that we use no zero padding (P=0), that the filter size is F=5, and that the stride is S=2. The output volume would therefore have spatial size (11-5)/2+1 = 4, giving a volume with width and height of 4. The activation map in the output volume (call it V), would then look as follows (only some of the elements are computed in this example):
-
예시 Conv Layer레이어 . 입력 볼륨 X의 모양이 X.shape: (11,11,4)라고 가정합니다. 또한 제로 패딩(P=0)을 사용하지 않고 필터 크기는 F=5이고 보폭은 S=2라고 가정합니다. 따라서 출력 볼륨은 공간 크기(11-5)/2+1 = 4를 가지며 너비와 높이가 4인 볼륨을 제공합니다. 출력 볼륨(V라고 함)의 활성화 맵은 다음과 같습니다(단지 이 예에서는 일부 요소가 계산됩니다.)
-
V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
-
V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
-
V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
-
V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0
Remember that in numpy, the operation * above denotes elementwise multiplication between the arrays. Notice also that the weight vector W0 is the weight vector of that neuron and b0 is the bias. Here, W0 is assumed to be of shape W0.shape: (5,5,4), since the filter size is 5 and the depth of the input volume is 4. Notice that at each point, we are computing the dot product as seen before in ordinary neural networks. Also, we see that we are using the same weight and bias (due to parameter sharing), and where the dimensions along the width are increasing in steps of 2 (i.e. the stride). To construct a second activation map in the output volume, we would have:
- numpy에서 위의 연산 *은 배열 간의 요소별 곱셈을 나타냅니다. 또한 가중치 벡터 W0는 해당 뉴런의 가중치 벡터이고 b0은 편향입니다. 여기서 W0는 모양이 W0.shape: (5,5,4)라고 가정합니다. 필터 크기가 5이고 입력 볼륨의 깊이가 4이기 때문입니다. 각 지점에서 다음과 같이 내적을 계산하고 있습니다. 일반 신경망에서 이전에 본 적이 있습니다. 또한 동일한 가중치와 편향(파라미터 공유로 인해)을 사용하고 있으며 너비에 따른 치수가 2단계(즉, 보폭)로 증가하고 있음을 알 수 있습니다. 출력 볼륨에서 두 번째 활성화 맵을 구성하려면 다음이 필요합니다.
<!-- -->
-
V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1
-
V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1
-
V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1
-
V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1
- V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1 (example of going
along y)
- V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1 (or along both)
where we see that we are indexing into the second depth dimension in V (at index 1) because we are computing the second activation map, and that a different set of parameters (W1) is now used. In the example above, we are for brevity leaving out some of the other operations the Conv Layer would perform to fill the other parts of the output array V. Additionally, recall that these activation maps are often followed elementwise through an activation function such as ReLU, but this is not shown here.
- 여기서 우리는 두 번째 활성화 맵을 계산하고 있기 때문에 V의 두 번째 깊이 차원(인덱스 1)으로 인덱싱하고 있으며 이제 다른 매개변수 세트(W1)가 사용됨을 알 수 있습니다. 위의 예에서 우리는 Conv Layer가 출력 배열 V의 다른 부분을 채우기 위해 수행할 다른 작업 중 일부를 간략하게 생략했습니다. 또한 이러한 활성화 맵은 종종 ReLU와 같은 활성화 함수를 통해 요소별로 뒤따른다는 것을 기억하십시오. , 그러나 여기에 표시되지 않습니다.
Summary. To summarize, the Conv Layer:
-
Accepts a volume of size W1×H1×D1
-
Requires four hyperparameters:
-
Number of filters K
-
their spatial extent F
-
the stride S
-
the amount of zero padding P
-
-
Produces a volume of size W2×H2×D2 where
-
W2=(W1−F+2P)/S+1
-
H2=(H1−F+2P)/S+1 (i.e. width and height are computed equally by symmetry)
-
D2=K
-
-
With parameter sharing, it introduces F⋅F⋅D1 weights per filter, for a total of (F⋅F⋅D1)⋅K weights and K biases.
-
In the output volume, the d-th depth slice (of size W2×H2) is the result of performing a valid convolution of the d-th filter over the input volume with a stride of S, and then offset by d-th bias
A common setting of the hyperparameters is F=3,S=1,P=1. However, there are common conventions and rules of thumb that motivate these hyperparameters. See the ConvNet architectures section below.
-
W1×H1×D1 크기의 볼륨 수용
-
4개의 하이퍼파라미터가 필요합니다.
-
필터 수 K
-
필터 사이즈
-
보폭
-
Padding
-
-
W2×H2×D2 크기의 볼륨을 생성합니다. 여기서
-
W2=(W1−F+2P)/S+1
-
H2=(H1−F+2P)/S+1 (즉, 너비와 높이가 대칭에 의해 동일하게 계산됨)
-
D2=K
-
-
매개변수 공유를 통해 총 (F⋅F⋅D1)⋅K 가중치 및 K 편향에 대해 필터당 F⋅F⋅D1 가중치를 도입합니다.
-
출력 볼륨에서 d번째 깊이 슬라이스(크기 W2×H2)는 입력 볼륨에 대한 d번째 필터의 유효한 컨볼루션을 보폭 S로 수행한 다음 d번째만큼 오프셋한 결과입니다. 편견
-
하이퍼파라미터의 일반적인 설정은 F=3,S=1,P=1입니다. 그러나 이러한 하이퍼파라미터에 동기를 부여하는 일반적인 규칙과 경험 법칙이 있습니다. 아래의 ConvNet 아키텍처 섹션을 참조하세요.
Convolution Demo. Below is a running demo of a CONV layer. Since 3D volumes are hard to visualize, all the volumes (the input volume (in blue), the weight volumes (in red), the output volume (in green)) are visualized with each depth slice stacked in rows. The input volume is of size W1=5,H1=5,D1=3, and the CONV layer parameters are K=2,F=3,S=2,P=1. That is, we have two filters of size 3×3, and they are applied with a stride of 2. Therefore, the output volume size has spatial size (5 - 3 + 2)/2 + 1 = 3. Moreover, notice that a padding of P=1 is applied to the input volume, making the outer border of the input volume zero. The visualization below iterates over the output activations (green), and shows that each element is computed by elementwise multiplying the highlighted input (blue) with the filter (red), summing it up, and then offsetting the result by the bias.
- 컨볼루션 데모. 아래는 CONV 레이어의 실행 데모입니다. 3D 볼륨은 시각화하기 어렵기 때문에 모든 볼륨(입력 볼륨(파란색), 가중치 볼륨(빨간색), 출력 볼륨(녹색))은 각 깊이 슬라이스가 행으로 쌓인 상태로 시각화됩니다. 입력 볼륨의 크기는 W1=5,H1=5,D1=3이고 CONV 레이어 매개변수는 K=2,F=3,S=2,P=1입니다. 즉, 크기가 3×3인 두 개의 필터가 있고 stride는 2로 적용됩니다. 따라서 출력 볼륨 크기는 공간 크기가 (5 - 3 + 2)/2 + 1 = 3입니다. P=1의 패딩이 입력 볼륨에 적용되어 입력 볼륨의 외부 경계를 0으로 만듭니다. 아래의 시각화는 출력 활성화(녹색)를 반복하며 각 요소가 강조 표시된 입력(파란색)과 필터(빨간색)를 요소별로 곱하고 합산한 다음 바이어스로 결과를 상쇄하여 계산됨을 보여줍니다.
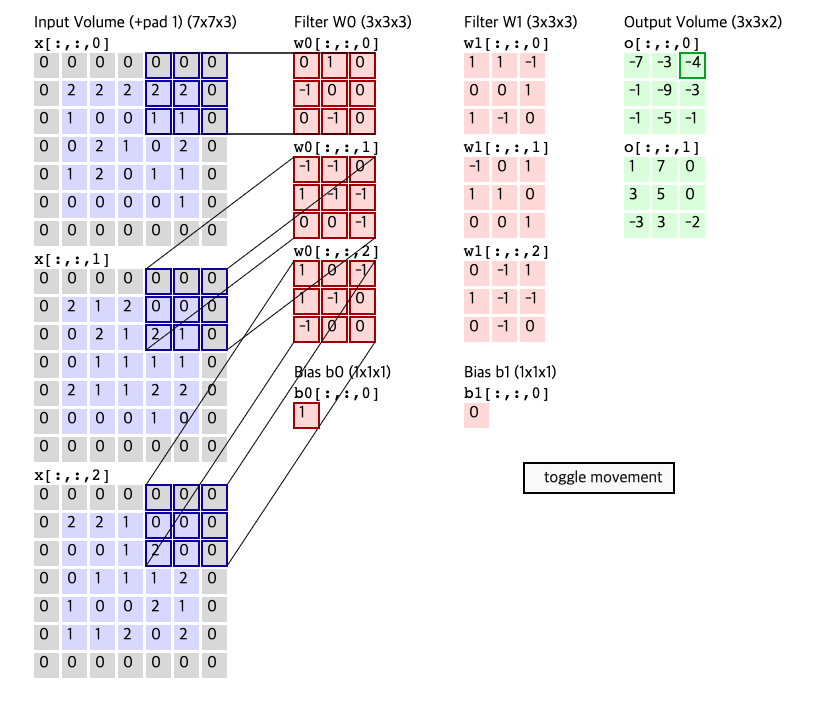
Implementation as Matrix Multiplication. Note that the convolution operation essentially performs dot products between the filters and local regions of the input. A common implementation pattern of the CONV layer is to take advantage of this fact and formulate the forward pass of a convolutional layer as one big matrix multiply as follows:
- 행렬 곱셈으로 구현. 컨볼루션 연산은 기본적으로 필터와 입력의 로컬 영역 간에 내적을 수행합니다. CONV 레이어의 일반적인 구현 패턴은 이 사실을 활용하고 다음과 같이 하나의 큰 행렬 곱으로 컨볼루션 레이어의 순방향 패스를 공식화하는 것입니다.
The local regions in the input image are stretched out into columns in an operation commonly called im2col. For example, if the input is [227x227x3] and it is to be convolved with 11x11x3 filters at stride 4, then we would take [11x11x3] blocks of pixels in the input and stretch each block into a column vector of size 11*11*3 = 363. Iterating this process in the input at stride of 4 gives (227-11)/4+1 = 55 locations along both width and height, leading to an output matrix X_col of im2col of size [363 x 3025], where every column is a stretched out receptive field and there are 55*55 = 3025 of them in total. Note that since the receptive fields overlap, every number in the input volume may be duplicated in multiple distinct columns.
- 입력 이미지의 로컬 영역은 일반적으로 im2col이라고 하는 작업에서 열로 확장됩니다. 예를 들어 입력이 [227x227x3]이고 스트라이드 4에서 11x11x3 필터로 컨볼루션되는 경우 입력에서 픽셀의 [11x11x3] 블록을 가져와 각 블록을 크기 11*11*의 열 벡터로 늘립니다. 3 = 363. 스트라이드 4의 입력에서 이 프로세스를 반복하면 너비와 높이를 따라 (227-11)/4+1 = 55개의 위치가 제공되며 크기가 [363 x 3025]인 im2col의 출력 행렬 X_col이 생성됩니다. 여기서 모든 열은 확장된 수용 필드이며 총 55*55 = 3025개가 있습니다. 수용 필드가 겹치기 때문에 입력 볼륨의 모든 숫자가 여러 개별 열에 복제될 수 있습니다.
The weights of the CONV layer are similarly stretched out into rows. For example, if there are 96 filters of size [11x11x3] this would give a matrix W_row of size [96 x 363].
- CONV 레이어의 가중치는 유사하게 행으로 늘어납니다. 예를 들어 크기가 [11x11x3]인 96개의 필터가 있는 경우 크기가 [96 x 363]인 행렬 W_row가 제공됩니다.
The result of a convolution is now equivalent to performing one large matrix multiply np.dot(W_row, X_col), which evaluates the dot product between every filter and every receptive field location. In our example, the output of this operation would be [96 x 3025], giving the output of the dot product of each filter at each location. The result must finally be reshaped back to its proper output dimension [55x55x96].
- 컨볼루션의 결과는 이제 모든 필터와 모든 수용 필드 위치 사이의 내적을 평가하는 하나의 큰 행렬 곱 np.dot(W_row, X_col)을 수행하는 것과 동일합니다. 이 예에서 이 작업의 출력은 [96 x 3025]가 되어 각 위치에서 각 필터의 내적 출력을 제공합니다. 결과는 최종적으로 적절한 출력 차원 [55x55x96]으로 다시 형성되어야 합니다.
This approach has the downside that it can use a lot of memory, since some values in the input volume are replicated multiple times in X_col. However, the benefit is that there are many very efficient implementations of Matrix Multiplication that we can take advantage of (for example, in the commonly used BLAS API). Moreover, the same im2col idea can be reused to perform the pooling operation, which we discuss next.
- 이 접근 방식은 입력 볼륨의 일부 값이 X_col에서 여러 번 복제되기 때문에 많은 메모리를 사용할 수 있다는 단점이 있습니다. 그러나 이점은 우리가 활용할 수 있는 매우 효율적인 행렬 곱셈 구현이 많다는 것입니다(예: 일반적으로 사용되는 BLAS API에서). 또한 동일한 im2col 아이디어를 재사용하여 다음에 논의할 풀링 작업을 수행할 수 있습니다.
Backpropagation. The backward pass for a convolution operation (for both the data and the weights) is also a convolution (but with spatially-flipped filters). This is easy to derive in the 1-dimensional case with a toy example (not expanded on for now).
- 역전파. 컨볼루션 연산의 역방향 패스(데이터와 가중치 모두에 대한)도 컨볼루션입니다(단, 공간적으로 뒤집힌 필터 사용). 이것은 장난감 예제(지금은 확장되지 않음)를 사용하여 1차원 사례에서 쉽게 파생할 수 있습니다.
1x1 convolution. As an aside, several papers use 1x1 convolutions, as first investigated by Network in Network. Some people are at first confused to see 1x1 convolutions especially when they come from signal processing background. Normally signals are 2-dimensional so 1x1 convolutions do not make sense (it’s just pointwise scaling). However, in ConvNets this is not the case because one must remember that we operate over 3-dimensional volumes, and that the filters always extend through the full depth of the input volume. For example, if the input is [32x32x3] then doing 1x1 convolutions would effectively be doing 3-dimensional dot products (since the input depth is 3 channels).
- 1x1 컨볼루션. 여담이지만 Network in Network에서 처음 조사한 것처럼 여러 논문에서 1x1 컨볼루션을 사용합니다. 일부 사람들은 특히 신호 처리 배경에서 온 경우 처음에는 1x1 컨볼루션을 보고 혼란스러워합니다. 일반적으로 신호는 2차원이므로 1x1 컨볼루션은 의미가 없습니다(그냥 점 단위 스케일링일 뿐입니다). 그러나 ConvNets에서는 3차원 볼륨에서 작동하고 필터가 항상 입력 볼륨의 전체 깊이를 통해 확장된다는 점을 기억해야 하기 때문에 그렇지 않습니다. 예를 들어 입력이 [32x32x3]인 경우 1x1 컨볼루션을 수행하는 것은 사실상 3차원 내적을 수행하는 것입니다(입력 깊이가 3채널이므로).
Dilated convolutions. A recent development (e.g. see paper by Fisher Yu and Vladlen Koltun) is to introduce one more hyperparameter to the CONV layer called the dilation. So far we’ve only discussed CONV filters that are contiguous. However, it’s possible to have filters that have spaces between each cell, called dilation. As an example, in one dimension a filter w of size 3 would compute over input x the following: w[0]*x[0] + w[1]*x[1] + w[2]*x[2]. This is dilation of 0. For dilation 1 the filter would instead compute w[0]*x[0] + w[1]*x[2] + w[2]*x[4]; In other words there is a gap of 1 between the applications. This can be very useful in some settings to use in conjunction with 0-dilated filters because it allows you to merge spatial information across the inputs much more agressively with fewer layers. For example, if you stack two 3x3 CONV layers on top of each other then you can convince yourself that the neurons on the 2nd layer are a function of a 5x5 patch of the input (we would say that the effective receptive field of these neurons is 5x5). If we use dilated convolutions then this effective receptive field would grow much quicker.
- 확장된 회선. 최근 개발(예: Fisher Yu 및 Vladlen Koltun의 논문 참조)은 확장이라고 하는 CONV 레이어에 하이퍼파라미터를 하나 더 도입하는 것입니다. 지금까지 우리는 연속적인 CONV 필터에 대해서만 논의했습니다. 그러나 확장이라고 하는 각 셀 사이에 공백이 있는 필터를 사용할 수 있습니다. 예를 들어, 1차원에서 크기가 3인 필터 w는 입력 x에 대해 다음을 계산합니다. w[0]*x[0] + w[1]*x[1] + w[2]*x[2] . 이것은 0의 팽창입니다. 팽창 1의 경우 필터는 대신 w[0]*x[0] + w[1]*x[2] + w[2]*x[4]를 계산합니다. 즉, 응용 프로그램 사이에 1의 간격이 있습니다. 이는 0-dilated 필터와 함께 사용하는 일부 설정에서 매우 유용할 수 있습니다. 더 적은 수의 레이어로 훨씬 더 공격적으로 입력 간에 공간 정보를 병합할 수 있기 때문입니다. 예를 들어, 두 개의 3x3 CONV 레이어를 서로 쌓으면 두 번째 레이어의 뉴런이 입력의 5x5 패치의 함수임을 확신할 수 있습니다. 5x5). 확장된 컨볼루션을 사용하면 이 효과적인 수용 필드가 훨씬 빠르게 성장할 것입니다.
2.2 Pooling Layer
It is common to periodically insert a Pooling layer in-between successive Conv layers in a ConvNet architecture. Its function is to progressively reduce the spatial size of the representation to reduce the amount of parameters and computation in the network, and hence to also control overfitting. The Pooling Layer operates independently on every depth slice of the input and resizes it spatially, using the MAX operation. The most common form is a pooling layer with filters of size 2x2 applied with a stride of 2 downsamples every depth slice in the input by 2 along both width and height, discarding 75% of the activations. Every MAX operation would in this case be taking a max over 4 numbers (little 2x2 region in some depth slice). The depth dimension remains unchanged. More generally, the pooling layer:
-
ConvNet 아키텍처에서 연속적인 Conv 레이어 사이에 주기적으로 Pooling 레이어를 삽입하는 것이 일반적입니다. 그 기능은 표현의 공간 크기를 점진적으로 줄여 네트워크에서 매개변수 및 계산의 양을 줄이고 따라서 과적합을 제어하는 것입니다. 풀링 레이어는 입력의 모든 깊이 슬라이스에서 독립적으로 작동하고 MAX 작업을 사용하여 공간적으로 크기를 조정합니다. 가장 일반적인 형태는 2x2 크기의 필터가 적용된 풀링 레이어로 스트라이드 2로 입력의 모든 깊이 슬라이스를 너비와 높이를 따라 2씩 다운샘플링하여 활성화의 75%를 버립니다. 이 경우 모든 MAX 작업은 4개 이상의 숫자(일부 깊이 슬라이스의 작은 2x2 영역)에서 최대값을 취합니다. 깊이 치수는 변경되지 않습니다. 보다 일반적으로 풀링 계층은 다음을 수행합니다.
-
Accepts a volume of size W1×H1×D1
-
Requires two hyperparameters:
-
their spatial extent F,
-
the stride S,
-
해석
-
W1 H1 D1 있음
-
파라미터 요구
-
필터 사이즈 F
-
보폭
-
-
Produces a volume of size W2×H2×D2 where:
-
W2=(W1−F)/S+1
-
H2=(H1−F)/S+1
-
D2=D1
-
-
Introduces zero parameters since it computes a fixed function of the input
-
For Pooling layers, it is not common to pad the input using zero-padding.
해석
-
W2×H2×D2 크기의 볼륨을 생성합니다.
-
W2=(W1−F)/S+1
-
H2=(H1−F)/S+1
-
D2=D1
-
-
입력의 고정 함수를 계산하므로 제로 매개변수를 도입합니다.
-
풀링 레이어의 경우 제로 패딩을 사용하여 입력을 패딩하는 것은 일반적이지 않습니다.
It is worth noting that there are only two commonly seen variations of the max pooling layer found in practice: A pooling layer with F=3,S=2 (also called overlapping pooling), and more commonly F=2,S=2. Pooling sizes with larger receptive fields are too destructive.
- F=3,S=2(중복 풀링이라고도 함) 및 더 일반적으로 F=2,S=2인 풀링 레이어의 두 가지 일반적으로 볼 수 있는 최대 풀링 레이어 변형이 실제로 발견된다는 점은 주목할 가치가 있습니다. 더 큰 수용 필드가 있는 풀링 크기는 너무 파괴적입니다.
General pooling. In addition to max pooling, the pooling units can also perform other functions, such as average pooling or even L2-norm pooling. Average pooling was often used historically but has recently fallen out of favor compared to the max pooling operation, which has been shown to work better in practice.
- 일반 풀링. 최대 풀링 외에도 풀링 장치는 평균 풀링 또는 L2 표준 풀링과 같은 다른 기능도 수행할 수 있습니다. 평균 풀링은 역사적으로 자주 사용되었지만 실제로는 더 잘 작동하는 것으로 나타난 최대 풀링 작업에 비해 최근 인기가 떨어졌습니다.
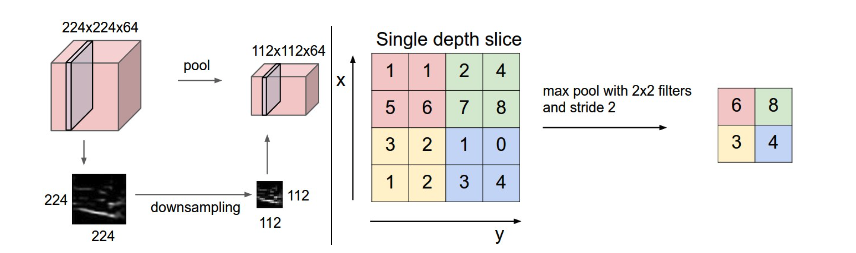
Pooling layer downsamples the volume spatially, independently in each depth slice of the input volume. Left: In this example, the input volume of size [224x224x64] is pooled with filter size 2, stride 2 into output volume of size [112x112x64]. Notice that the volume depth is preserved. Right: The most common downsampling operation is max, giving rise to max pooling, here shown with a stride of 2. That is, each max is taken over 4 numbers (little 2x2 square).
- 풀링 계층은 입력 볼륨의 각 깊이 슬라이스에서 독립적으로 볼륨을 공간적으로 다운샘플링합니다. 왼쪽: 이 예에서 [224x224x64] 크기의 입력 볼륨은 필터 크기 2, 스트라이드 2로 [112x112x64] 크기의 출력 볼륨으로 풀링됩니다. 볼륨 깊이가 유지됩니다. 오른쪽: 가장 일반적인 다운샘플링 작업은 최대이며 최대 풀링이 발생합니다. 여기서는 보폭이 2로 표시됩니다. 즉, 각 최대값은 4개의 숫자(작은 2x2 정사각형)에 사용됩니다.
Backpropagation. Recall from the backpropagation chapter that the backward pass for a max(x, y) operation has a simple interpretation as only routing the gradient to the input that had the highest value in the forward pass. Hence, during the forward pass of a pooling layer it is common to keep track of the index of the max activation (sometimes also called the switches) so that gradient routing is efficient during backpropagation.
- 전파. 역전파 장에서 max(x, y) 연산에 대한 역방향 전달은 순방향 전달에서 가장 높은 값을 가진 입력으로 경사도를 라우팅하는 것으로 간단하게 해석된다는 점을 상기하십시오. 따라서 풀링 레이어의 순방향 전달 중에 최대 활성화 인덱스(종종 스위치라고도 함)를 추적하여 역전파 중에 그래디언트 라우팅이 효율적이 되도록 하는 것이 일반적입니다.
Getting rid of pooling. Many people dislike the pooling operation and think that we can get away without it. For example, Striving for Simplicity: The All Convolutional Net proposes to discard the pooling layer in favor of architecture that only consists of repeated CONV layers. To reduce the size of the representation they suggest using larger stride in CONV layer once in a while. Discarding pooling layers has also been found to be important in training good generative models, such as variational autoencoders (VAEs) or generative adversarial networks (GANs). It seems likely that future architectures will feature very few to no pooling layers.
- 풀링 제거. 많은 사람들이 풀링 작업을 싫어하고 풀링 작업 없이도 문제를 해결할 수 있다고 생각합니다. 예를 들어, 단순성을 위한 노력: All Convolutional Net은 반복되는 CONV 레이어로만 구성된 아키텍처를 위해 풀링 레이어를 폐기할 것을 제안합니다. 표현의 크기를 줄이기 위해 그들은 때때로 CONV 레이어에서 더 큰 보폭을 사용할 것을 제안합니다. VAE(Variational Autoencoder) 또는 GAN(Generative Adversarial Networks)과 같은 우수한 생성 모델을 훈련하는 데 풀링 레이어를 폐기하는 것도 중요한 것으로 밝혀졌습니다. 미래의 아키텍처에는 풀링 레이어가 거의 없거나 아예 없을 것 같습니다.
2.3 Normalization Layer
Many types of normalization layers have been proposed for use in ConvNet architectures, sometimes with the intentions of implementing inhibition schemes observed in the biological brain. However, these layers have since fallen out of favor because in practice their contribution has been shown to be minimal, if any. For various types of normalizations, see the discussion in Alex Krizhevsky’s cuda-convnet library API.
- 많은 유형의 정규화 계층이 ConvNet 아키텍처에서 사용하기 위해 제안되었으며 때로는 생물학적 뇌에서 관찰되는 억제 체계를 구현하려는 의도가 있습니다. 그러나 이러한 레이어는 실제로 기여도가 미미한 것으로 나타났기 때문에 인기가 떨어졌습니다. 다양한 유형의 정규화에 대해서는 Alex Krizhevsky의 cuda-convnet 라이브러리 API의 토론을 참조하세요.
2.4 Fully-connected layer
Neurons in a fully connected layer have full connections to all activations in the previous layer, as seen in regular Neural Networks. Their activations can hence be computed with a matrix multiplication followed by a bias offset. See the Neural Network section of the notes for more information.
- 완전히 연결된 계층의 뉴런은 일반 신경망에서 볼 수 있듯이 이전 계층의 모든 활성화에 대해 완전히 연결되어 있습니다. 따라서 이들의 활성화는 행렬 곱셈과 바이어스 오프셋으로 계산할 수 있습니다. 자세한 내용은 노트의 신경망 섹션을 참조하십시오.
2.4 Converting FC layers to CONV layers
It is worth noting that the only difference between FC and CONV layers is that the neurons in the CONV layer are connected only to a local region in the input, and that many of the neurons in a CONV volume share parameters. However, the neurons in both layers still compute dot products, so their functional form is identical. Therefore, it turns out that it’s possible to convert between FC and CONV layers:
해석
-
FC와 CONV 레이어의 유일한 차이점은 CONV 레이어의 뉴런이 입력의 로컬 영역에만 연결되고 CONV 볼륨의 많은 뉴런이 매개변수를 공유한다는 점입니다. 그러나 두 계층의 뉴런은 여전히 내적을 계산하므로 기능적 형태가 동일합니다. 따라서 FC와 CONV 레이어 간에 변환이 가능하다는 것이 밝혀졌습니다.
-
For any CONV layer there is an FC layer that implements the same forward function. The weight matrix would be a large matrix that is mostly zero except for at certain blocks (due to local connectivity) where the weights in many of the blocks are equal (due to parameter sharing).
-
Conversely, any FC layer can be converted to a CONV layer. For example, an FC layer with K=4096 that is looking at some input volume of size 7×7×512 can be equivalently expressed as a CONV layer with F=7,P=0,S=1,K=4096. In other words, we are setting the filter size to be exactly the size of the input volume, and hence the output will simply be 1×1×4096 since only a single depth column “fits” across the input volume, giving identical result as the initial FC layer.
해석
-
모든 CONV 계층에는 동일한 순방향 기능을 구현하는 FC 계층이 있습니다. 가중치 행렬은 (파라미터 공유로 인해) 많은 블록의 가중치가 동일한 특정 블록(로컬 연결로 인해)을 제외하고 대부분 0인 큰 행렬입니다.
-
반대로 모든 FC 레이어를 CONV 레이어로 변환할 수 있습니다. 예를 들어, 7×7×512 크기의 일부 입력 볼륨을 보고 있는 K=4096인 FC 레이어는 F=7,P=0,S=1,K=4096인 CONV 레이어로 동등하게 표현할 수 있습니다. 즉, 필터 크기를 정확히 입력 볼륨의 크기로 설정하고 있으므로 출력은 단순히 1×1×4096이 됩니다. 입력 볼륨 전체에 하나의 깊이 열만 "적합"하므로 다음과 같은 결과를 제공합니다. 초기 FC 레이어.
FC->CONV conversion. Of these two conversions, the ability to convert an FC layer to a CONV layer is particularly useful in practice. Consider a ConvNet architecture that takes a 224x224x3 image, and then uses a series of CONV layers and POOL layers to reduce the image to an activations volume of size 7x7x512 (in an AlexNet architecture that we’ll see later, this is done by use of 5 pooling layers that downsample the input spatially by a factor of two each time, making the final spatial size 224/2/2/2/2/2 = 7). From there, an AlexNet uses two FC layers of size 4096 and finally the last FC layers with 1000 neurons that compute the class scores. We can convert each of these three FC layers to CONV layers as described above:
-
FC->CONV 변환. 이 두 변환 중에서 FC 레이어를 CONV 레이어로 변환하는 기능은 실제로 특히 유용합니다. 224x224x3 이미지를 가져온 다음 일련의 CONV 레이어와 POOL 레이어를 사용하여 이미지를 7x7x512 크기의 활성화 볼륨으로 줄이는 ConvNet 아키텍처를 고려하십시오(나중에 보게 될 AlexNet 아키텍처에서 이것은 다음을 사용하여 수행됩니다. 입력을 매번 2배씩 공간적으로 다운샘플링하여 최종 공간 크기를 224/2/2/2/2/2 = 7로 만드는 5개의 풀링 레이어. 여기에서 AlexNet은 크기가 4096인 두 개의 FC 계층과 마지막으로 클래스 점수를 계산하는 1000개의 뉴런이 있는 마지막 FC 계층을 사용합니다. 위에서 설명한 대로 이 세 개의 FC 레이어를 각각 CONV 레이어로 변환할 수 있습니다.
-
Replace the first FC layer that looks at [7x7x512] volume with a CONV layer that uses filter size F=7, giving output volume [1x1x4096].
-
Replace the second FC layer with a CONV layer that uses filter size F=1, giving output volume [1x1x4096]
-
Replace the last FC layer similarly, with F=1, giving final output [1x1x1000]
해석
-
7x7x512] 볼륨을 보는 첫 번째 FC 레이어를 필터 크기 F=7을 사용하여 출력 볼륨 [1x1x4096]을 제공하는 CONV 레이어로 교체합니다.
-
두 번째 FC 레이어를 필터 크기 F=1을 사용하는 CONV 레이어로 교체하여 출력 볼륨 [1x1x4096]을 제공합니다.
- 마찬가지로 마지막 FC 레이어를 F=1로 교체하여 최종 출력 [1x1x1000]을 제공합니다.
Each of these conversions could in practice involve manipulating (e.g. reshaping) the weight matrix W in each FC layer into CONV layer filters. It turns out that this conversion allows us to “slide” the original ConvNet very efficiently across many spatial positions in a larger image, in a single forward pass.
- 이러한 각 변환에는 실제로 각 FC 레이어의 가중치 행렬 W를 CONV 레이어 필터로 조작(예: 재구성)하는 작업이 포함될 수 있습니다. 이 변환을 통해 원본 ConvNet을 단일 포워드 패스에서 더 큰 이미지의 많은 공간 위치에 걸쳐 매우 효율적으로 "슬라이드"할 수 있습니다.
For example, if 224x224 image gives a volume of size [7x7x512] - i.e. a reduction by 32, then forwarding an image of size 384x384 through the converted architecture would give the equivalent volume in size [12x12x512], since 384/32 = 12. Following through with the next 3 CONV layers that we just converted from FC layers would now give the final volume of size [6x6x1000], since (12 - 7)/1 + 1 = 6. Note that instead of a single vector of class scores of size [1x1x1000], we’re now getting an entire 6x6 array of class scores across the 384x384 image.
- 예를 들어, 224x224 이미지가 [7x7x512] 크기의 볼륨을 제공하는 경우(즉, 32로 축소) 변환된 아키텍처를 통해 384x384 크기의 이미지를 전달하면 384/32 = 12이므로 크기가 [12x12x512]인 해당 볼륨이 제공됩니다. FC 레이어에서 방금 변환한 다음 3개의 CONV 레이어를 따라가면 (12 - 7)/1 + 1 = 6이므로 크기가 [6x6x1000]인 최종 볼륨이 제공됩니다. 클래스 점수의 단일 벡터 대신 크기가 [1x1x1000]인 경우 이제 384x384 이미지에서 클래스 점수의 전체 6x6 배열을 얻습니다.
Evaluating the original ConvNet (with FC layers) independently across 224x224 crops of the 384x384 image in strides of 32 pixels gives an identical result to forwarding the converted ConvNet one time.
- 32픽셀의 스트라이드에서 384x384 이미지의 224x224 크롭에서 원본 ConvNet(FC 레이어 포함)을 독립적으로 평가하면 변환된 ConvNet을 한 번 전달하는 것과 동일한 결과를 얻을 수 있습니다.
Naturally, forwarding the converted ConvNet a single time is much more efficient than iterating the original ConvNet over all those 36 locations, since the 36 evaluations share computation. This trick is often used in practice to get better performance, where for example, it is common to resize an image to make it bigger, use a converted ConvNet to evaluate the class scores at many spatial positions and then average the class scores.
- 당연히 변환된 ConvNet을 한 번 전달하는 것이 36개의 평가가 계산을 공유하기 때문에 원래 ConvNet을 36개 위치 모두에서 반복하는 것보다 훨씬 효율적입니다. 이 트릭은 실제로 더 나은 성능을 얻기 위해 자주 사용됩니다. 예를 들어 이미지 크기를 조정하여 더 크게 만들고 변환된 ConvNet을 사용하여 많은 공간 위치에서 클래스 점수를 평가한 다음 클래스 점수를 평균하는 것이 일반적입니다.
Lastly, what if we wanted to efficiently apply the original ConvNet over the image but at a stride smaller than 32 pixels? We could achieve this with multiple forward passes. For example, note that if we wanted to use a stride of 16 pixels we could do so by combining the volumes received by forwarding the converted ConvNet twice: First over the original image and second over the image but with the image shifted spatially by 16 pixels along both width and height.
- 마지막으로 원본 ConvNet을 이미지 위에 효율적으로 적용하고 싶지만 보폭이 32픽셀보다 작으면 어떻게 될까요? 여러 순방향 패스를 사용하여 이를 달성할 수 있습니다. 예를 들어, 16픽셀의 보폭을 사용하려는 경우 변환된 ConvNet을 두 번 전달하여 받은 볼륨을 결합하여 그렇게 할 수 있습니다. 첫 번째는 원본 이미지 위에, 두 번째는 이미지 위에 있지만 공간적으로 16픽셀 이동된 이미지를 사용합니다. 너비와 높이를 모두 따라.
An IPython Notebook on Net Surgery shows how to perform the conversion in practice, in code (using Caffe)
- Net Surgery의 IPython Notebook은 코드에서 실제로 변환을 수행하는 방법을 보여줍니다(Caffe 사용).
3. ConvNet Architectures
We have seen that Convolutional Networks are commonly made up of only three layer types: CONV, POOL (we assume Max pool unless stated otherwise) and FC (short for fully-connected). We will also explicitly write the RELU activation function as a layer, which applies elementwise non-linearity. In this section we discuss how these are commonly stacked together to form entire ConvNets.
- Convolutional Networks는 일반적으로 CONV, POOL(달리 명시하지 않는 한 Max pool로 가정) 및 FC(완전 연결의 줄임말)의 세 가지 계층 유형으로만 구성됩니다. 또한 요소별 비선형성을 적용하는 RELU 활성화 함수를 레이어로 명시적으로 작성합니다. 이 섹션에서는 전체 ConvNet을 형성하기 위해 일반적으로 함께 쌓이는 방법에 대해 설명합니다.
3.1 Layer Patterns
The most common form of a ConvNet architecture stacks a few CONV-RELU layers, follows them with POOL layers, and repeats this pattern until the image has been merged spatially to a small size. At some point, it is common to transition to fully-connected layers. The last fully-connected layer holds the output, such as the class scores. In other words, the most common ConvNet architecture follows the pattern:
- ConvNet 아키텍처의 가장 일반적인 형태는 몇 개의 CONV-RELU 레이어를 쌓고 POOL 레이어를 따라 이미지가 공간적으로 작은 크기로 병합될 때까지 이 패턴을 반복합니다. 어느 시점에서 완전 연결 계층으로 전환하는 것이 일반적입니다. 마지막 완전 연결 계층은 클래스 점수와 같은 출력을 보유합니다. 즉, 가장 일반적인 ConvNet 아키텍처는 다음 패턴을 따릅니다.
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC
where the * indicates repetition, and the POOL? indicates an optional pooling layer. Moreover, N >= 0 (and usually N <= 3), M >= 0, K >= 0 (and usually K < 3). For example, here are some common ConvNet architectures you may see that follow this pattern:
-
여기서 *는 반복을 나타내고 POOL? 선택적 풀링 계층을 나타냅니다. 또한 N >= 0(및 일반적으로 N <= 3), M >= 0, K >= 0(및 일반적으로 K < 3)입니다. 예를 들어 다음은 이 패턴을 따르는 몇 가지 일반적인 ConvNet 아키텍처입니다.
-
INPUT -> FC, implements a linear classifier. Here N = M = K = 0.
-
INPUT -> CONV -> RELU -> FC
-
INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC. Here we see that there is a single CONV layer between every POOL layer.
-
INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]*3 -> [FC -> RELU]*2 -> FC Here we see two CONV layers stacked before every POOL layer. This is generally a good idea for larger and deeper networks, because multiple stacked CONV layers can develop more complex features of the input volume before the destructive pooling operation.
해석
-
INPUT -> FC, 선형 분류기를 구현합니다. 여기서 N = M = K = 0입니다.
-
입력 -> 변환 -> RELU -> FC
-
입력 -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC. 여기에서 모든 POOL 레이어 사이에 단일 CONV 레이어가 있음을 알 수 있습니다.
-
INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]*3 -> [FC -> RELU]*2 -> FC 여기에서 모든 POOL 레이어 앞에 쌓인 두 개의 CONV 레이어를 볼 수 있습니다. 이것은 일반적으로 더 크고 깊은 네트워크에 좋은 아이디어입니다. 다중 스택 CONV 레이어는 파괴적인 풀링 작업 전에 입력 볼륨의 더 복잡한 기능을 개발할 수 있기 때문입니다.
Prefer a stack of small filter CONV to one large receptive field CONV layer. Suppose that you stack three 3x3 CONV layers on top of each other (with non-linearities in between, of course). In this arrangement, each neuron on the first CONV layer has a 3x3 view of the input volume. A neuron on the second CONV layer has a 3x3 view of the first CONV layer, and hence by extension a 5x5 view of the input volume. Similarly, a neuron on the third CONV layer has a 3x3 view of the 2nd CONV layer, and hence a 7x7 view of the input volume. Suppose that instead of these three layers of 3x3 CONV, we only wanted to use a single CONV layer with 7x7 receptive fields. These neurons would have a receptive field size of the input volume that is identical in spatial extent (7x7), but with several disadvantages. First, the neurons would be computing a linear function over the input, while the three stacks of CONV layers contain non-linearities that make their features more expressive. Second, if we suppose that all the volumes have C channels, then it can be seen that the single 7x7 CONV layer would contain C×(7×7×C)=49C\^2 parameters, while the three 3x3 CONV layers would only contain 3×(C×(3×3×C))=27C\^2 parameters. Intuitively, stacking CONV layers with tiny filters as opposed to having one CONV layer with big filters allows us to express more powerful features of the input, and with fewer parameters. As a practical disadvantage, we might need more memory to hold all the intermediate CONV layer results if we plan to do backpropagation.
- 하나의 큰 수용 필드 CONV 레이어보다 작은 필터 CONV 스택을 선호합니다. 세 개의 3x3 CONV 레이어를 서로 위에 쌓는다고 가정해 보겠습니다(물론 그 사이에는 비선형성이 있습니다). 이 배열에서 첫 번째 CONV 레이어의 각 뉴런은 입력 볼륨의 3x3 보기를 갖습니다. 두 번째 CONV 레이어의 뉴런은 첫 번째 CONV 레이어의 3x3 보기를 가지고 있으므로 확장하여 입력 볼륨의 5x5 보기를 갖습니다. 마찬가지로 세 번째 CONV 레이어의 뉴런은 두 번째 CONV 레이어의 3x3 뷰를 가지므로 입력 볼륨의 7x7 뷰를 갖습니다. 3x3 CONV의 세 레이어 대신 7x7 수용 필드가 있는 단일 CONV 레이어만 사용하고 싶다고 가정합니다. 이러한 뉴런은 공간 범위(7x7)가 동일하지만 몇 가지 단점이 있는 입력 볼륨의 수용 필드 크기를 갖습니다. 첫째, 뉴런은 입력에 대해 선형 함수를 계산하는 반면 3개의 CONV 레이어 스택에는 기능을 더욱 표현력 있게 만드는 비선형성이 포함되어 있습니다. 둘째, 모든 볼륨에 C 채널이 있다고 가정하면 단일 7x7 CONV 레이어에는 C×(7×7×C)=49C\^2 매개변수가 포함되는 반면 3개의 3x3 CONV 레이어에는 매개변수만 포함된다는 것을 알 수 있습니다. 3×(C×(3×3×C))=27C\^2 매개변수. 직관적으로 큰 필터가 있는 하나의 CONV 레이어를 갖는 것과 반대로 작은 필터가 있는 CONV 레이어를 쌓으면 더 적은 매개변수로 입력의 더 강력한 기능을 표현할 수 있습니다. 실질적인 단점으로, 역전파를 수행할 계획이라면 모든 중간 CONV 레이어 결과를 저장하기 위해 더 많은 메모리가 필요할 수 있습니다.
Recent departures. It should be noted that the conventional paradigm of a linear list of layers has recently been challenged, in Google’s Inception architectures and also in current (state of the art) Residual Networks from Microsoft Research Asia. Both of these (see details below in case studies section) feature more intricate and different connectivity structures.
- 계층의 선형 목록에 대한 기존 패러다임은 최근 Google의 Inception 아키텍처와 Microsoft Research Asia의 현재(최첨단) Residual Networks에서 도전을 받았습니다. 이 두 가지(아래 사례 연구 섹션의 세부 정보 참조)는 더 복잡하고 서로 다른 연결 구조를 특징으로 합니다.
In practice: use whatever works best on ImageNet. If you’re feeling a bit of a fatigue in thinking about the architectural decisions, you’ll be pleased to know that in 90% or more of applications you should not have to worry about these. I like to summarize this point as “don’t be a hero”: Instead of rolling your own architecture for a problem, you should look at whatever architecture currently works best on ImageNet, download a pretrained model and finetune it on your data. You should rarely ever have to train a ConvNet from scratch or design one from scratch. I also made this point at the Deep Learning school.
- ImageNet에서 가장 잘 작동하는 것을 사용하십시오. 아키텍처 결정에 대해 생각하는 데 약간의 피로를 느끼고 있다면 애플리케이션의 90% 이상에서 이에 대해 걱정할 필요가 없다는 사실에 기뻐할 것입니다. 저는 이 점을 "영웅이 되지 마십시오"라고 요약하고 싶습니다. 문제를 해결하기 위해 자신의 아키텍처를 롤링하는 대신 현재 ImageNet에서 가장 잘 작동하는 아키텍처를 살펴보고 사전 훈련된 모델을 다운로드하고 데이터에 맞게 미세 조정해야 합니다. ConvNet을 처음부터 훈련시키거나 처음부터 디자인해야 하는 경우는 거의 없습니다. 딥 러닝 학교에서도 이 점을 지적했습니다.
3.2 Layer Sizing Patterns
Until now we’ve omitted mentions of common hyperparameters used in each of the layers in a ConvNet. We will first state the common rules of thumb for sizing the architectures and then follow the rules with a discussion of the notation:
- 지금까지 우리는 ConvNet의 각 레이어에서 사용되는 일반적인 하이퍼파라미터에 대한 언급을 생략했습니다. 먼저 아키텍처 크기 조정에 대한 일반적인 경험 법칙을 설명한 다음 표기법에 대한 논의와 함께 규칙을 따릅니다.
The input layer (that contains the image) should be divisible by 2 many times. Common numbers include 32 (e.g. CIFAR-10), 64, 96 (e.g. STL-10), or 224 (e.g. common ImageNet ConvNets), 384, and 512.
- 이미지가 포함된 입력 레이어는 여러 번 2로 나눌 수 있어야 합니다. 일반적인 숫자에는 32(예: CIFAR-10), 64, 96(예: STL-10) 또는 224(예: 일반적인 ImageNet ConvNets), 384 및 512가 포함됩니다.
The conv layers should be using small filters (e.g. 3x3 or at most 5x5), using a stride of S=1, and crucially, padding the input volume with zeros in such way that the conv layer does not alter the spatial dimensions of the input. That is, when F=3, then using P=1 will retain the original size of the input. When F=5, P=2. For a general F, it can be seen that P=(F−1)/2 preserves the input size. If you must use bigger filter sizes (such as 7x7 or so), it is only common to see this on the very first conv layer that is looking at the input image.
- conv 레이어는 작은 필터(예: 3x3 또는 최대 5x5)를 사용하고 스트라이드 S=1을 사용하며 결정적으로 conv 레이어가 입력의 공간 차원을 변경하지 않는 방식으로 입력 볼륨을 0으로 패딩해야 합니다. . 즉, F=3일 때 P=1을 사용하면 입력의 원래 크기가 유지됩니다. F=5일 때, P=2. 일반적인 F의 경우 P=(F−1)/2가 입력 크기를 유지함을 알 수 있습니다. 더 큰 필터 크기(예: 7x7 정도)를 사용해야 하는 경우 입력 이미지를 보는 첫 번째 conv 레이어에서만 이를 보는 것이 일반적입니다.
The pool layers are in charge of downsampling the spatial dimensions of the input. The most common setting is to use max-pooling with 2x2 receptive fields (i.e. F=2), and with a stride of 2 (i.e. S=2). Note that this discards exactly 75% of the activations in an input volume (due to downsampling by 2 in both width and height). Another slightly less common setting is to use 3x3 receptive fields with a stride of 2, but this makes “fitting” more complicated (e.g., a 32x32x3 layer would require zero padding to be used with a max-pooling layer with 3x3 receptive field and stride 2). It is very uncommon to see receptive field sizes for max pooling that are larger than 3 because the pooling is then too lossy and aggressive. This usually leads to worse performance.
- 풀 레이어는 입력의 공간 차원을 다운샘플링하는 역할을 합니다. 가장 일반적인 설정은 2x2 수용 필드(즉, F=2)와 2의 보폭(즉, S=2)으로 최대 풀링을 사용하는 것입니다. 이것은 입력 볼륨에서 활성화의 정확히 75%를 버립니다(너비와 높이 모두에서 2로 다운샘플링했기 때문). 또 다른 약간 덜 일반적인 설정은 스트라이드가 2인 3x3 수용 필드를 사용하는 것이지만 이렇게 하면 "피팅"이 더 복잡해집니다(예: 32x32x3 레이어는 3x3 수용 필드 및 보폭이 있는 최대 풀링 레이어와 함께 사용하려면 제로 패딩이 필요함) 2). 풀링이 너무 손실이 많고 공격적이기 때문에 3보다 큰 최대 풀링에 대한 수용 필드 크기를 보는 것은 매우 드문 일입니다. 이로 인해 일반적으로 성능이 저하됩니다.
Reducing sizing headaches. The scheme presented above is pleasing because all the CONV layers preserve the spatial size of their input, while the POOL layers alone are in charge of down-sampling the volumes spatially. In an alternative scheme where we use strides greater than 1 or don’t zero-pad the input in CONV layers, we would have to very carefully keep track of the input volumes throughout the CNN architecture and make sure that all strides and filters “work out”, and that the ConvNet architecture is nicely and symmetrically wired.
- 사이징 두통 감소. 위에 제시된 체계는 모든 CONV 레이어가 입력의 공간 크기를 유지하는 반면 POOL 레이어만 볼륨을 공간적으로 다운 샘플링하기 때문에 만족스럽습니다. 1보다 큰 보폭을 사용하거나 CONV 레이어의 입력을 제로 패딩하지 않는 대체 방식에서는 CNN 아키텍처 전체에서 입력 볼륨을 매우 주의 깊게 추적하고 모든 보폭과 필터가 "작동하는지" 확인해야 합니다. out”, 그리고 ConvNet 아키텍처가 멋지고 대칭적으로 연결되어 있습니다.
Why use stride of 1 in CONV? Smaller strides work better in practice. Additionally, as already mentioned stride 1 allows us to leave all spatial down-sampling to the POOL layers, with the CONV layers only transforming the input volume depth-wise.
- CONV에서 stride 1을 사용하는 이유는 무엇입니까? 더 작은 보폭은 실제로 더 잘 작동합니다. 또한 이미 언급한 것처럼 stride 1을 사용하면 모든 공간 다운 샘플링을 POOL 레이어에 남겨두고 CONV 레이어는 입력 볼륨을 깊이 방향으로만 변환합니다.
Why use padding? In addition to the aforementioned benefit of keeping the spatial sizes constant after CONV, doing this actually improves performance. If the CONV layers were to not zero-pad the inputs and only perform valid convolutions, then the size of the volumes would reduce by a small amount after each CONV, and the information at the borders would be “washed away” too quickly.
- 패딩을 사용하는 이유는 무엇입니까? 앞서 언급한 CONV 이후 공간 크기를 일정하게 유지하는 이점 외에도 이렇게 하면 실제로 성능이 향상됩니다. CONV 레이어가 입력을 제로 패딩하지 않고 유효한 컨볼루션만 수행하면 각 CONV 후 볼륨 크기가 약간 줄어들고 경계의 정보가 너무 빨리 "씻겨 나갈" 것입니다.
Compromising based on memory constraints. In some cases (especially early in the ConvNet architectures), the amount of memory can build up very quickly with the rules of thumb presented above. For example, filtering a 224x224x3 image with three 3x3 CONV layers with 64 filters each and padding 1 would create three activation volumes of size [224x224x64]. This amounts to a total of about 10 million activations, or 72MB of memory (per image, for both activations and gradients). Since GPUs are often bottlenecked by memory, it may be necessary to compromise. In practice, people prefer to make the compromise at only the first CONV layer of the network. For example, one compromise might be to use a first CONV layer with filter sizes of 7x7 and stride of 2 (as seen in a ZF net). As another example, an AlexNet uses filter sizes of 11x11 and stride of 4.
- 메모리 제약 조건에 따른 타협. 경우에 따라(특히 초기 ConvNet 아키텍처에서) 위에 제시된 경험 법칙에 따라 메모리 양이 매우 빠르게 증가할 수 있습니다. 예를 들어 224x224x3 이미지를 각각 64개의 필터와 패딩 1이 있는 3개의 3x3 CONV 레이어로 필터링하면 [224x224x64] 크기의 활성화 볼륨 3개가 생성됩니다. 이것은 총 약 1,000만 건의 활성화 또는 72MB의 메모리에 해당합니다(활성화 및 기울기 모두에 대해 이미지당). GPU는 종종 메모리 병목 현상이 발생하므로 타협이 필요할 수 있습니다. 실제로 사람들은 네트워크의 첫 번째 CONV 계층에서만 타협하는 것을 선호합니다. 예를 들어 한 가지 절충안은 필터 크기가 7x7이고 보폭이 2인 첫 번째 CONV 레이어를 사용하는 것입니다(ZF 네트워크에서 볼 수 있음). 또 다른 예로 AlexNet은 11x11의 필터 크기와 4의 보폭을 사용합니다.
3.3 Case studies
There are several architectures in the field of Convolutional Networks that have a name. The most common are:
- 컨볼루션 네트워크 분야에는 이름을 가진 여러 아키텍처가 있습니다. 가장 일반적인 것은 다음과 같습니다:
LeNet. The first successful applications of Convolutional Networks were developed by Yann LeCun in 1990’s. Of these, the best known is the LeNet architecture that was used to read zip codes, digits, etc.
- 르넷. Convolutional Networks의 첫 번째 성공적인 애플리케이션은 1990년대에 Yann LeCun에 의해 개발되었습니다. 이 중 가장 잘 알려진 것은 우편 번호, 숫자 등을 읽는 데 사용된 LeNet 아키텍처입니다.
AlexNet. The first work that popularized Convolutional Networks in Computer Vision was the AlexNet, developed by Alex Krizhevsky, Ilya Sutskever and Geoff Hinton. The AlexNet was submitted to the ImageNet ILSVRC challenge in 2012 and significantly outperformed the second runner-up (top 5 error of 16% compared to runner-up with 26% error). The Network had a very similar architecture to LeNet, but was deeper, bigger, and featured Convolutional Layers stacked on top of each other (previously it was common to only have a single CONV layer always immediately followed by a POOL layer).
- AlexNet. 컴퓨터 비전에서 컨볼루션 네트워크를 대중화한 첫 번째 작업은 Alex Krizhevsky, Ilya Sutskever 및 Geoff Hinton이 개발한 AlexNet입니다. AlexNet은 2012년 ImageNet ILSVRC 챌린지에 제출되었으며 두 번째 준우승자를 크게 능가했습니다(상위 5개 오류 16%, 준우승 오류 26%). 네트워크는 LeNet과 매우 유사한 아키텍처를 가지고 있었지만 더 깊고 더 컸으며 서로 위에 쌓인 컨볼루션 레이어를 특징으로 했습니다(이전에는 단일 CONV 레이어만 있고 항상 바로 뒤에 POOL 레이어가 오는 것이 일반적이었습니다).
ZF Net. The ILSVRC 2013 winner was a Convolutional Network from Matthew Zeiler and Rob Fergus. It became known as the ZFNet (short for Zeiler & Fergus Net). It was an improvement on AlexNet by tweaking the architecture hyperparameters, in particular by expanding the size of the middle convolutional layers and making the stride and filter size on the first layer smaller.
- ZF넷. ILSVRC 2013 우승자는 Matthew Zeiler와 Rob Fergus의 Convolutional Network였습니다. ZFNet(Zeiler & Fergus Net의 약자)으로 알려지게 되었습니다. 특히 중간 컨볼루션 레이어의 크기를 확장하고 첫 번째 레이어의 보폭과 필터 크기를 더 작게 만들어 아키텍처 하이퍼파라미터를 조정함으로써 AlexNet에서 개선되었습니다.
GoogLeNet. The ILSVRC 2014 winner was a Convolutional Network from Szegedy et al. from Google. Its main contribution was the development of an Inception Module that dramatically reduced the number of parameters in the network (4M, compared to AlexNet with 60M). Additionally, this paper uses Average Pooling instead of Fully Connected layers at the top of the ConvNet, eliminating a large amount of parameters that do not seem to matter much. There are also several followup versions to the GoogLeNet, most recently Inception-v4.
- GoogLeNet. ILSVRC 2014 우승자는 Szegedy et al.의 Convolutional Network였습니다. 구글에서. 주요 기여는 네트워크의 매개변수 수를 극적으로 줄이는 Inception Module의 개발이었습니다(AlexNet의 60M에 비해 4M). 또한 이 논문에서는 ConvNet의 상단에 있는 Fully Connected 레이어 대신 Average Pooling을 사용하여 별로 중요해 보이지 않는 많은 양의 매개변수를 제거합니다. 또한 GoogLeNet에 대한 몇 가지 후속 버전, 가장 최근에는 Inception-v4가 있습니다.
VGGNet. The runner-up in ILSVRC 2014 was the network from Karen Simonyan and Andrew Zisserman that became known as the VGGNet. Its main contribution was in showing that the depth of the network is a critical component for good performance. Their final best network contains 16 CONV/FC layers and, appealingly, features an extremely homogeneous architecture that only performs 3x3 convolutions and 2x2 pooling from the beginning to the end. Their pretrained model is available for plug and play use in Caffe. A downside of the VGGNet is that it is more expensive to evaluate and uses a lot more memory and parameters (140M). Most of these parameters are in the first fully connected layer, and it was since found that these FC layers can be removed with no performance downgrade, significantly reducing the number of necessary parameters.
- VGGNet. ILSVRC 2014의 준우승자는 VGGNet으로 알려지게 된 Karen Simonyan과 Andrew Zisserman의 네트워크였습니다. 그것의 주요 기여는 네트워크의 깊이가 좋은 성능을 위한 중요한 구성 요소임을 보여주는 것이었습니다. 그들의 최종 최고의 네트워크에는 16개의 CONV/FC 레이어가 포함되어 있으며 처음부터 끝까지 3x3 컨볼루션과 2x2 풀링만 수행하는 매우 균일한 아키텍처가 특징입니다. 사전 훈련된 모델은 Caffe에서 플러그 앤 플레이로 사용할 수 있습니다. VGGNet의 단점은 평가 비용이 더 많이 들고 훨씬 더 많은 메모리와 매개변수(140M)를 사용한다는 것입니다. 이러한 매개변수의 대부분은 첫 번째 완전 연결 계층에 있으며 이후 이러한 FC 계층은 성능 저하 없이 제거할 수 있으므로 필요한 매개변수의 수를 크게 줄일 수 있습니다.
ResNet. Residual Network developed by Kaiming He et al. was the winner of ILSVRC 2015. It features special skip connections and a heavy use of batch normalization. The architecture is also missing fully connected layers at the end of the network. The reader is also referred to Kaiming’s presentation (video, slides), and some recent experiments that reproduce these networks in Torch. ResNets are currently by far state of the art Convolutional Neural Network models and are the default choice for using ConvNets in practice (as of May 10, 2016). In particular, also see more recent developments that tweak the original architecture from Kaiming He et al. Identity Mappings in Deep Residual Networks (published March 2016).
- ResNet. Kaiming He 등이 개발한 잔여 네트워크. ILSVRC 2015의 우승자였습니다. 특수 건너뛰기 연결과 배치 정규화를 많이 사용하는 것이 특징입니다. 이 아키텍처에는 네트워크 끝에 있는 완전히 연결된 계층도 없습니다. 독자는 또한 Kaiming의 프레젠테이션(비디오, 슬라이드) 및 Torch에서 이러한 네트워크를 재현하는 일부 최근 실험을 참조합니다. ResNet은 현재 최첨단 Convolutional Neural Network 모델이며 실제로 ConvNet을 사용하기 위한 기본 선택입니다(2016년 5월 10일 현재). 특히 Kaiming He et al.의 원래 아키텍처를 수정한 최신 개발도 참조하십시오. Deep Residual Networks의 ID 매핑(2016년 3월 게시).
VGGNet in detail. Lets break down the VGGNet in more detail as a case study. The whole VGGNet is composed of CONV layers that perform 3x3 convolutions with stride 1 and pad 1, and of POOL layers that perform 2x2 max pooling with stride 2 (and no padding). We can write out the size of the representation at each step of the processing and keep track of both the representation size and the total number of weights:
- VGGNet 자세히. 사례 연구로 VGGNet을 더 자세히 분석해 보겠습니다. 전체 VGGNet은 스트라이드 1과 패드 1로 3x3 컨볼루션을 수행하는 CONV 레이어와 스트라이드 2(및 패딩 없음)로 2x2 최대 풀링을 수행하는 POOL 레이어로 구성됩니다. 처리의 각 단계에서 표현의 크기를 기록하고 표현 크기와 총 가중치 수를 모두 추적할 수 있습니다.
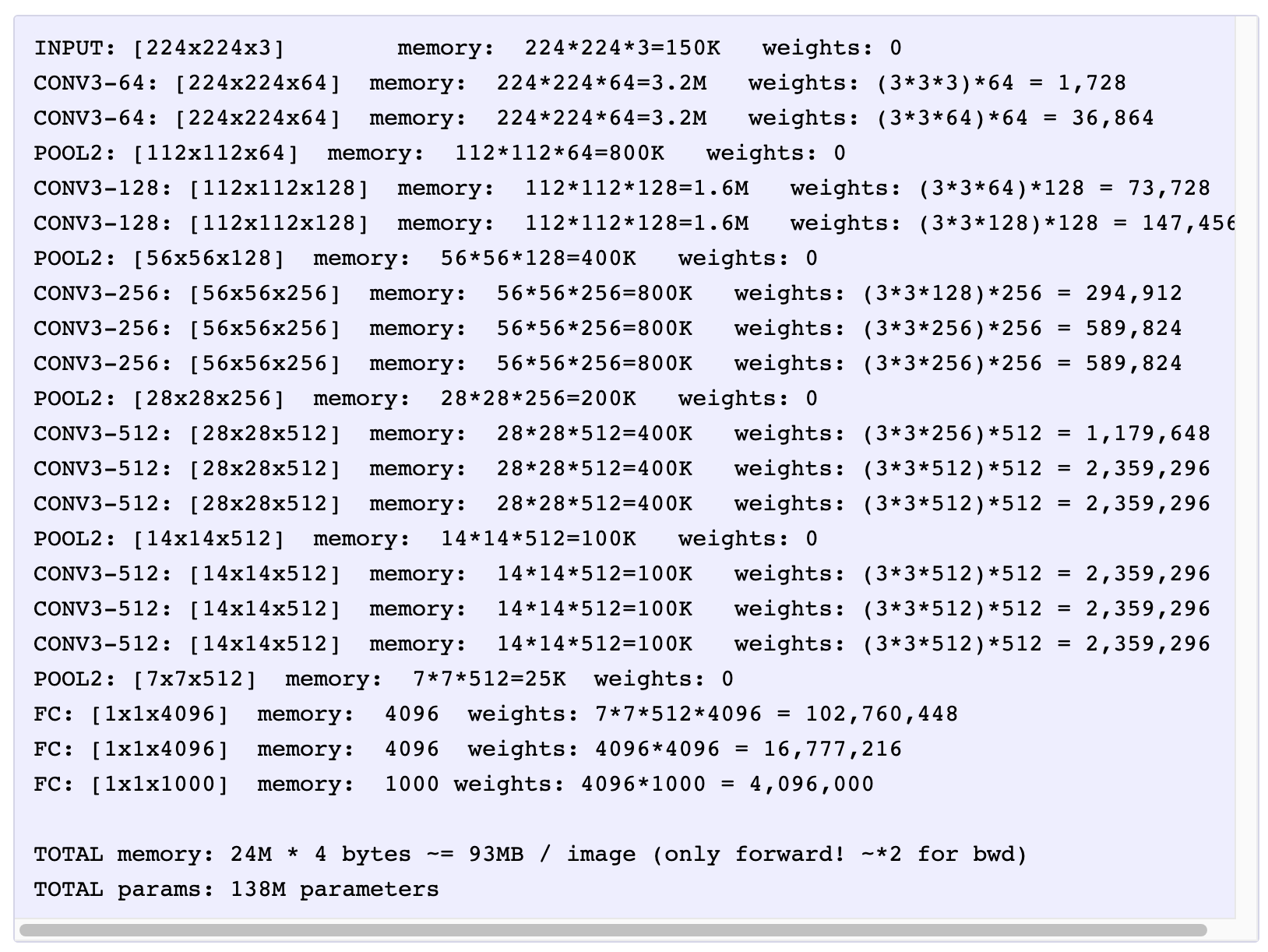
As is common with Convolutional Networks, notice that most of the memory (and also compute time) is used in the early CONV layers, and that most of the parameters are in the last FC layers. In this particular case, the first FC layer contains 100M weights, out of a total of 140M.
- 컨볼루션 네트워크에서 흔히 볼 수 있듯이 대부분의 메모리(및 컴퓨팅 시간)가 초기 CONV 레이어에서 사용되며 대부분의 매개변수가 마지막 FC 레이어에 있음을 알 수 있습니다. 이 특별한 경우 첫 번째 FC 레이어는 총 140M 중 100M 가중치를 포함합니다
3.4 Computational Considerations
The largest bottleneck to be aware of when constructing ConvNet architectures is the memory bottleneck. Many modern GPUs have a limit of 3/4/6GB memory, with the best GPUs having about 12GB of memory. There are three major sources of memory to keep track of:
- ConvNet 아키텍처를 구성할 때 알아야 할 가장 큰 병목 현상은 메모리 병목 현상입니다. 많은 최신 GPU의 메모리는 3/4/6GB로 제한되며 가장 좋은 GPU의 메모리는 약 12GB입니다. 추적해야 할 세 가지 주요 메모리 소스가 있습니다.
From the intermediate volume sizes: These are the raw number of activations at every layer of the ConvNet, and also their gradients (of equal size). Usually, most of the activations are on the earlier layers of a ConvNet (i.e. first Conv Layers). These are kept around because they are needed for backpropagation, but a clever implementation that runs a ConvNet only at test time could in principle reduce this by a huge amount, by only storing the current activations at any layer and discarding the previous activations on layers below.
- 중간 볼륨 크기에서: 이것은 ConvNet의 모든 계층에서 활성화의 원시 수와 기울기(동일한 크기)입니다. 일반적으로 대부분의 활성화는 ConvNet의 초기 레이어(즉, 첫 번째 Conv 레이어)에 있습니다. 이들은 역전파에 필요하기 때문에 유지되지만 테스트 시간에만 ConvNet을 실행하는 영리한 구현은 원칙적으로 현재 활성화만 저장하고 아래 계층에서 이전 활성화를 폐기함으로써 이를 크게 줄일 수 있습니다. .
From the parameter sizes: These are the numbers that hold the network parameters, their gradients during backpropagation, and commonly also a step cache if the optimization is using momentum, Adagrad, or RMSProp. Therefore, the memory to store the parameter vector alone must usually be multiplied by a factor of at least 3 or so.
- 매개변수 크기에서: 이것은 네트워크 매개변수, 역전파 동안의 기울기, 최적화가 모멘텀, Adagrad 또는 RMSProp을 사용하는 경우 일반적으로 단계 캐시를 보유하는 숫자입니다. 따라서 매개변수 벡터만 저장하는 메모리는 일반적으로 최소 3배 정도 곱해야 합니다.
Every ConvNet implementation has to maintain miscellaneous memory, such as the image data batches, perhaps their augmented versions, etc.
- 모든 ConvNet 구현은 이미지 데이터 배치, 확장된 버전 등과 같은 기타 메모리를 유지해야 합니다.
Once you have a rough estimate of the total number of values (for activations, gradients, and misc), the number should be converted to size in GB. Take the number of values, multiply by 4 to get the raw number of bytes (since every floating point is 4 bytes, or maybe by 8 for double precision), and then divide by 1024 multiple times to get the amount of memory in KB, MB, and finally GB. If your network doesn’t fit, a common heuristic to “make it fit” is to decrease the batch size, since most of the memory is usually consumed by the activations
- 값의 총 수(활성화, 기울기 및 기타)에 대한 대략적인 추정치를 얻은 후에는 그 수를 크기(GB)로 변환해야 합니다. 값의 수를 취하고 4를 곱하여 원시 바이트 수를 얻은 다음(모든 부동 소수점은 4바이트이므로 배정밀도의 경우 8을 곱할 수 있음) 1024로 여러 번 나누어 메모리 양(KB)을 얻습니다. MB, 마지막으로 GB. 네트워크가 적합하지 않은 경우 "적합하게 만드는" 일반적인 휴리스틱은 일반적으로 대부분의 메모리가 활성화에 의해 소비되기 때문에 배치 크기를 줄이는 것입니다.
Additional references
- https://cs231n.github.io