cs231n 강의 노트 5장 Neural Networks Part 1: Setting up the Architecture

Neural Networks Part 1: Setting up the Architecture

1. Quick intro without brain analogies

It is possible to introduce neural networks without appealing to brain analogies. In the section on linear classification we computed scores for different visual categories given the image using the formula s=Wx , where W was a matrix and x was an input column vector containing all pixel data of the image. In the case of CIFAR-10, x is a [3072x1] column vector, and W is a [10x3072] matrix, so that the output scores is a vector of 10 class scores.

해석

• 큰 생각없이 신경망을 도입하는 것이 가능합니다. 선형 분류 섹션에서 공식 s=Wx를 사용하여 이미지가 주어진 다양한 시각적 범주에 대한 점수를 계산할것이다. 여기서 W는 행렬이고 x는 이미지의 모든 픽셀 데이터를 포함하는 입력 열 벡터입니다. CIFAR-10의 경우 x는 [3072x1] 열 벡터이고 W는 [10x3072] 행렬이므로 출력 점수는 클래스 점수 10개의 벡터가 됩니다.

An example neural network would instead compute s=W2max(0,W1x). Here, W1 could be, for example, a [100x3072] matrix transforming the image into a 100-dimensional intermediate vector. The function max(0,−) is a non-linearity that is applied elementwise. There are several choices we could make for the non-linearity (which we’ll study below), but this one is a common choice and simply thresholds all activations that are below zero to zero. Finally, the matrix W2 would then be of size [10x100], so that we again get 10 numbers out that we interpret as the class scores. Notice that the non-linearity is critical computationally - if we left it out, the two matrices could be collapsed to a single matrix, and therefore the predicted class scores would again be a linear function of the input. The non-linearity is where we get the wiggle. The parameters W2,W1 are learned with stochastic gradient descent, and their gradients are derived with chain rule (and computed with backpropagation).

해석

• 예제 신경망은 대신 s=W2max(0,W1x)를 계산합니다. 여기서 W1은 예를 들어 이미지를 100차원 중간 벡터로 변환하는 [100x3072] 행렬일 수 있습니다.
• 함수 max(0,-)는 요소별로 적용되는 비선형성입니다(활성화 함수). 비선형성에 대해 우리가 할 수 있는 몇 가지 선택이 있지만(relu, tanh, etc) 이것은 일반적인 선택이며 단순히 0에서 0 미만인 모든 활성화 임계값을 지정합니다.
• 마지막으로 행렬 W2의 크기는 [10x100]이므로 클래스 점수로 해석하는 10개의 숫자를 다시 얻습니다. 비선형성은 계산이 중요합니다. 비선형성을 생략하면 두 행렬이 단일 행렬로 축소될 수 있으므로 예측된 클래스 점수는 다시 입력의 선형 함수가 됩니다.
• 비선형성은 우리가 흔들림을 얻는 곳입니다. 매개변수 W2, W1은 확률적 경사하강법으로 학습되고 해당 경사도는 체인 규칙으로 도출됩니다(역전파로 계산됨).

A three-layer neural network could analogously look like s=W3max(0,W2max(0,W1x)), where all of W3,W2,W1 are parameters to be learned. The sizes of the intermediate hidden vectors are hyperparameters of the network and we’ll see how we can set them later. Lets now look into how we can interpret these computations from the neuron/network perspective.

해석

• 3개의 계층 신경망은 유사하게 s=W3max(0,W2max(0,W1x))처럼 보일 수 있습니다. 여기서 모든 W3,W2,W1은 학습할 매개변수입니다.
• 중간 히든 벡터의 크기는 네트워크의 하이퍼파라미터이며 나중에 설정하는 방법을 살펴보겠습니다.
• 이제 뉴런/네트워크 관점에서 이러한 계산을 해석할 수 있는 방법을 살펴보겠습니다.

2. Modeling one neuron

The area of Neural Networks has originally been primarily inspired by the goal of modeling biological neural systems, but has since diverged and become a matter of engineering and achieving good results in Machine Learning tasks. Nonetheless, we begin our discussion with a very brief and high-level description of the biological system that a large portion of this area has been inspired by.

• 신경망 영역은 원래 생물학적 신경 시스템을 모델링하는 목표에서 영감을 받았지만, 이후 기계 학습 작업에서 좋은 결과를 달성하고 엔지니어링의 문제가 되었습니다.
• 그럼에도 불구하고 우리는 이 분야의 많은 부분이 영감을 받은 생물학적 시스템에 대한 매우 간략하고 높은 수준의 설명으로 논의를 시작합니다.

2.1 Biological motivation and connections

The basic computational unit of the brain is a neuron. Approximately 86 billion neurons can be found in the human nervous system and they are connected with approximately 10^14 - 10^15 synapses.
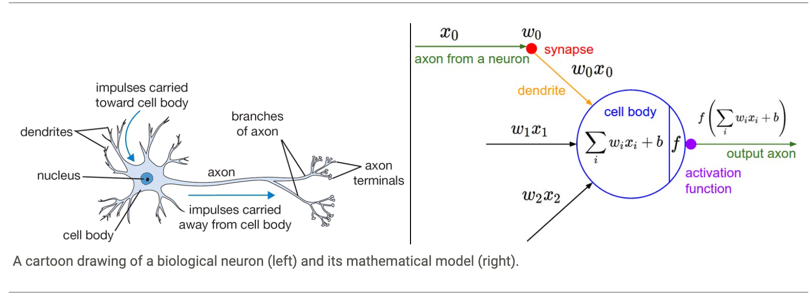
The diagram below shows a cartoon drawing of a biological neuron (left) and a common mathematical model (right)
Each neuron receives input signals from its dendrites and produces output signals along its (single) axon.
The axon eventually branches out and connects via synapses to dendrites of other neurons.
In the computational model of a neuron, the signals that travel along the axons (e.g. x0) interact multiplicatively (e.g. w0x0) with the dendrites of the other neuron based on the synaptic strength at that synapse (e.g. w0).
The idea is that the synaptic strengths (the weights w) are learnable and control the strength of influence (and its direction: excitory (positive weight) or inhibitory (negative weight)) of one neuron on another.
In the basic model, the dendrites carry the signal to the cell body where they all get summed.
If the final sum is above a certain threshold, the neuron can fire, sending a spike along its axon.
In the computational model, we assume that the precise timings of the spikes do not matter, and that only the frequency of the firing communicates information.
Based on this rate code interpretation, we model the firing rate of the neuron with an activation function f, which represents the frequency of the spikes along the axon.
Historically, a common choice of activation function is the sigmoid function σ, since it takes a real-valued input (the signal strength after the sum) and squashes it to range between 0 and 1. We will see details of these activation functions later in this section.

해석

• 뇌의 기본 계산 단위는 뉴런입니다. 인간의 신경계에는 약 860억 개의 뉴런이 있으며 약 10^14 - 10^15개의 시냅스와 연결되어 있습니다.
• 아래 다이어그램은 생물학적 뉴런(왼쪽)과 일반적인 수학적 모델(오른쪽)의 그림을 보여줍니다.
• 각 뉴런은 수상돌기로부터 입력 신호를 받고 (단일) 축삭을 따라 출력 신호를 생성합니다.
• 축삭은 결국 분기되어 시냅스를 통해 다른 뉴런의 수상돌기에 연결됩니다.
• 뉴런의 계산 모델에서 축삭(예: x0)을 따라 이동하는 신호는 해당 시냅스(예: w0)의 시냅스 강도를 기반으로 다른 뉴런의 수상돌기와 승산적으로(예: w0x0) 상호 작용합니다.
• 아이디어는 시냅스 강도(가중치 w)가 학습 가능하고 다른 뉴런에 대한 영향의 강도(및 그 방향: 흥분성(양성 가중치) 또는 억제성(음성 가중치))를 제어한다는 것입니다.
• 기본 모델에서 수상돌기는 모두 합산되는 세포체로 신호를 전달합니다.
• 최종 합계가 특정 임계값을 초과하면 뉴런이 발화하여 축삭을 따라 스파이크를 보낼 수 있습니다.
• 계산 모델에서 스파이크의 정확한 타이밍은 중요하지 않으며 발사 빈도만이 정보를 전달한다고 가정합니다.
• 이 속도 코드 해석을 기반으로 축삭을 따라 스파이크의 빈도를 나타내는 활성화 함수 f로 뉴런의 발사 속도를 모델링합니다.
• 역사적으로 활성화 함수의 일반적인 선택은 시그모이드 함수 σ입니다. 이는 실제 값 입력(합계 이후의 신호 강도)을 취하고 이를 0과 1 사이의 범위로 스쿼시하기 때문입니다. 이러한 활성화 함수에 대한 자세한 내용은 나중에 살펴보겠습니다. 이 구역.

An example code for forward-propagating a single neuron might look as follows:

import numpy as np
import math
class Neuron(object):
    # ... 
    def forward(self, inputs):
        """ assume inputs and weights are 1-D numpy arrays and bias is a number """
        cell_body_sum = np.sum(inputs * self.weights) + self.bias
        firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum))  # sigmoid activation function
        return firing_rate

In other words, each neuron performs a dot product with the input and its weights, adds the bias and applies the non-linearity (or activation function), in this case the sigmoid σ(x)=1/(1+e−x). We will go into more details about different activation functions at the end of this section.

• 즉, 각 뉴런은 입력과 가중치로 내적을 수행하고 바이어스를 추가하고 비선형성(또는 활성화 함수)을 적용합니다. 이 경우 시그모이드 σ(x)=1/(1+e−x).
• 이 섹션의 끝에서 다양한 활성화 기능에 대해 자세히 알아볼 것입니다.

Coarse model.
It’s important to stress that this model of a biological neuron is very coarse:
For example, there are many different types of neurons, each with different properties. The dendrites in biological neurons perform complex nonlinear computations.
The synapses are not just a single weight, they’re a complex non-linear dynamical system.
The exact timing of the output spikes in many systems is known to be important, suggesting that the rate code approximation may not hold.
Due to all these and many other simplifications, be prepared to hear groaning sounds from anyone with some neuroscience background if you draw analogies between Neural Networks and real brains.
See this review (pdf), or more recently this review if you are interested.

• 거친 모델. 이 생물학적 뉴런 모델이 매우 거칠다는 점을 강조하는 것이 중요합니다.
• 예를 들어, 각각 다른 특성을 가진 다양한 유형의 뉴런이 있습니다. 생물학적 뉴런의 수상돌기는 복잡한 비선형 계산을 수행합니다.
• 시냅스는 단순한 가중치가 아니라 복잡한 비선형 동적 시스템입니다. 많은 시스템에서 출력 스파이크의 정확한 타이밍은 중요한 것으로 알려져 있으며, 이는 비율 코드 근사치가 유지되지 않을 수 있음을 시사합니다.
• 이러한 모든 단순화와 다른 많은 단순화로 인해 신경망과 실제 두뇌 사이에 유추를 그리는 경우 신경 과학 배경을 가진 사람의 힘듦 소리를 들을 준비를 하십시오.
• 이 리뷰(pdf)를 참조하거나 관심이 있는 경우 최근 이 리뷰를 참조하십시오.

2.2 Single neuron as a linear classifier

The mathematical form of the model Neuron’s forward computation might look familiar to you. As we saw with linear classifiers, a neuron has the capacity to “like” (activation near one) or “dislike” (activation near zero) certain linear regions of its input space. Hence, with an appropriate loss function on the neuron’s output, we can turn a single neuron into a linear classifier:

• 모델 Neuron의 순방향 계산의 수학적 형식이 친숙해 보일 수 있습니다.
• 선형 분류기에서 보았듯이 뉴런은 입력 공간의 특정 선형 영역을 “좋아”(1에 가까운 활성화) 또는 “싫어요”(0에 가까운 활성화)할 수 있는 능력이 있습니다.
• 따라서 뉴런의 출력에 대한 적절한 손실 함수를 사용하여 단일 뉴런을 선형 분류기로 전환할 수 있습니다.

2.2.1 Binary Softmax classifier.

For example, we can interpret \(\sigma(\sum_iw_ix_i + b)\)to be the probability of one of the classes \(P(y_i = 1 \mid x_i; w) \).
The probability of the other class would be \(P(y_i = 0 \mid x_i; w) = 1 - P(y_i = 1 \mid x_i; w) \), since they must sum to one.
With this interpretation, we can formulate the cross-entropy loss as we have seen in the Linear Classification section, and optimizing it would lead to a binary Softmax classifier (also known as logistic regression).
Since the sigmoid function is restricted to be between 0-1, the predictions of this classifier are based on whether the output of the neuron is greater than 0.5.

• 이진 Softmax 분류기. 예를 들어, \(\sigma(\sum_iw_ix_i + b)\)를 클래스 \(P(y_i = 1 \mid x_i; w) \)중 하나의 확률로 해석할 수 있습니다.
• 다른 클래스의 확률은 합이 1이어야 하므로 \(P(y_i = 0 \mid x_i; w) = 1 - P(y_i = 1 \mid x_i; w) \),입니다.
• 이 해석을 통해 선형 분류 섹션에서 본 교차 엔트로피 손실을 공식화할 수 있으며 이를 최적화하면 이진 Softmax 분류기(로지스틱 회귀라고도 함)로 이어질 수 있습니다.
• 시그모이드 함수는 0-1 사이로 제한되므로 이 분류기의 예측은 뉴런의 출력이 0.5보다 큰지 여부를 기반으로 합니다.

2.2.2 Binary SVM classifier.

Alternatively, we could attach a max-margin hinge loss to the output of the neuron and train it to become a binary Support Vector Machine.

• 이진 SVM 분류기. 또는 뉴런의 출력에 최대 마진 경첩 손실을 첨부하고 이진 지원 벡터 머신이 되도록 훈련할 수 있습니다.

2.2.3 Regularization interpretation.

The regularization loss in both SVM/Softmax cases could in this biological view be interpreted as gradual forgetting, since it would have the effect of driving all synaptic weights w towards zero after every parameter update.

• 정규화 해석. SVM/Softmax 사례 모두에서 정규화 손실은 모든 매개변수 업데이트 후에 모든 시냅스 가중치 w를 0으로 유도하는 효과가 있기 때문에 이 생물학적 관점에서 점진적인 망각으로 해석될 수 있습니다.

2.3 Commonly used activation functions

Every activation function (or non-linearity) takes a single number and performs a certain fixed mathematical operation on it. There are several activation functions you may encounter in practice:

• 모든 활성화 함수(또는 비선형성)는 단일 숫자를 사용하여 특정 고정 수학 연산을 수행합니다. 실제로 접할 수 있는 몇 가지 활성화 함수가 있습니다.

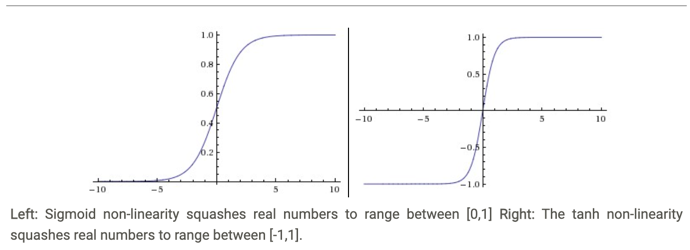
2.3.1 Sigmoid.

The sigmoid non-linearity has the mathematical form \(\sigma(x) = 1 / (1 + e^{-x})\) and is shown in the image above on the left. As alluded to in the previous section, it takes a real-valued number and “squashes” it into range between 0 and 1. In particular, large negative numbers become 0 and large positive numbers become 1. The sigmoid function has seen frequent use historically since it has a nice interpretation as the firing rate of a neuron: from not firing at all (0) to fully-saturated firing at an assumed maximum frequency (1). In practice, the sigmoid non-linearity has recently fallen out of favor and it is rarely ever used. It has two major drawbacks:

• 시그모이드
• 시그모이드 비선형성 수학적 형식은 \(\sigma(x) = 1 / (1 + e^{-x})\)이며 위의 왼쪽 이미지에 표시되어 있습니다.
• 이전 섹션에서 언급했듯이 실수 값을 가져와 0과 1 사이의 범위로 “압축”합니다. 특히 큰 음수는 0이 되고 큰 양수는 1이 됩니다.
• 시그모이드 함수는 역사적으로 자주 사용되었습니다. 그것은 뉴런의 발화 속도로 잘 해석되기 때문입니다.
• x가 음수로 가까워질 수 록 0으로 수렴하고, x가 양수로 갈 수 록 1로 수렴하게 된다.(기울기 손실로 일어날 수 있음)
• 실제로 시그모이드 비선형성은 최근 선호도가 떨어졌으며 거의 사용되지 않습니다. 두 가지 주요 단점이 있습니다.

Sigmoids saturate and kill gradients. A very undesirable property of the sigmoid neuron is that when the neuron’s activation saturates at either tail of 0 or 1, the gradient at these regions is almost zero. Recall that during backpropagation, this (local) gradient will be multiplied to the gradient of this gate’s output for the whole objective. Therefore, if the local gradient is very small, it will effectively “kill” the gradient and almost no signal will flow through the neuron to its weights and recursively to its data. Additionally, one must pay extra caution when initializing the weights of sigmoid neurons to prevent saturation. For example, if the initial weights are too large then most neurons would become saturated and the network will barely learn.

용어

• 포화된(saturated : 입력 값이 너무 크거나 작을 때 출력값 그래프의 기울기가 0에 가까워지는 현상 (활성화 함수에서))

• 극단적인 시그모이드는 기울기가 죽는다.
• 시그모이드 뉴런의 매우 바람직하지 않은 특성은 뉴런의 활성화가값이 입력값이 너무 작거나 매우 클 때 기울기는 거의 0이다.
• 역전파 동안 (로컬) 그래디언트는 전체 목표에 대한 이 게이트 출력의 그래디언트에 곱해집니다.(밑에 그럼 예시)
• 따라서 로컬 그래디언트가 매우 작으면 그래디언트를 효과적으로 “죽이고” 뉴런을 통해 가중치로, 재귀적으로 데이터로 신호가 거의 흐르지 않습니다.
• 또한 포화를 방지하기 위해 시그모이드 뉴런의 가중치를 초기화할 때 각별한 주의를 기울여야 합니다. 예를 들어, 초기 가중치가 너무 크면 대부분의 뉴런이 포화 상태가 되어 네트워크가 거의 학습하지 않습니다.

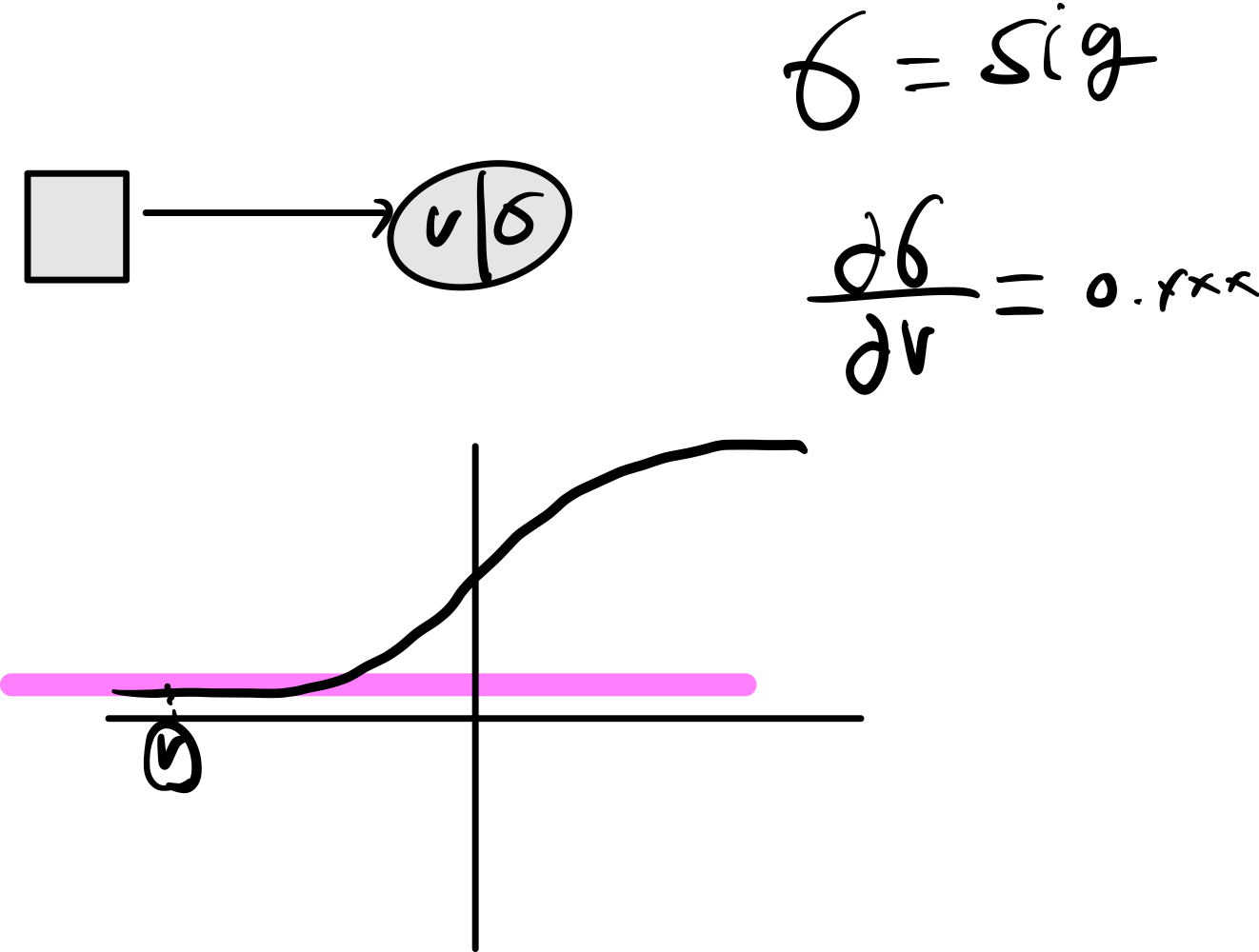
정리

• sigmoid 함수를 사용하면 극단적으로 값이 설정 될시 기울기가 죽는 현상이 발생한다.
• 기울기를 살리기 위해서는 적절한 가중치를 설정해야 한다.

Sigmoid outputs are not zero-centered.
This is undesirable since neurons in later layers of processing in a Neural Network (more on this soon) would be receiving data that is not zero-centered.
This has implications on the dynamics during gradient descent, because if the data coming into a neuron is always positive (e.g. x>0 elementwise in f=wTx+b)), then the gradient on the weights w will during backpropagation become either all be positive, or all negative (depending on the gradient of the whole expression f).
This could introduce undesirable zig-zagging dynamics in the gradient updates for the weights.
However, notice that once these gradients are added up across a batch of data the final update for the weights can have variable signs, somewhat mitigating this issue.
Therefore, this is an inconvenience but it has less severe consequences compared to the saturated activation problem above.

• 시그모이드 출력은 0 중심이 아닙니다.
• 이것은 Neural Network(곧 자세히 설명)에서 처리의 후반 계층에 있는 뉴런이 0 중심이 아닌 데이터를 수신하기 때문에 바람직하지 않습니다.
• 기울기가 감소 하는 동안 역학에 영향을 미칩니다. 왜냐하면 뉴런으로 들어오는 데이터가 항상 양수이면(예: f=wTx+b에서 요소별로 x>0) 역전파 동안 가중치 w의 기울기는 모두 양수 또는 모두 음수(전체 식 f의 기울기에 따라 다름).
• 이는 가중치에 대한 그래디언트 업데이트에서 바람직하지 않은 지그재그 역학을 도입할 수 있습니다.
• 그러나 이러한 기울기가 데이터 배치에 합산되면 가중치에 대한 최종 업데이트에 변수 부호가 있을 수 있으므로 이 문제가 어느 정도 완화될 수 있습니다.
• 따라서 이는 불편하지만 위의 포화 활성화 문제에 비해 덜 심각한 결과를 초래합니다.

정리

• 만약 0중심이 아니기 때문에 항상 양수를 바라보고 있다.
• 활성화 함수에서 나온 값은 다른 뉴런에 활성화 함수가 되기 때문에 무저건 양수인 값을 가지게 된다.
• 그럼( dL / dW == dL / df) 부호는 같아야한다.
• dl / df 부호를 따라가 전부 양수이거나, 전부 음수가 된다.

시그모이드는 문제점은 총 3가지가 있다. 시그모이드 극단적인 값사용, 0 중심이 아닌 값, exp 계산하는 비용이 많이 발생한다.

2.3.2 Tanh

The tanh non-linearity is shown on the image above on the right.
It squashes a real-valued number to the range [-1, 1]. Like the sigmoid neuron, its activations saturate, but unlike the sigmoid neuron its output is zero-centered.
Therefore, in practice the tanh non-linearity is always preferred to the sigmoid nonlinearity.
Also note that the tanh neuron is simply a scaled sigmoid neuron, in particular the following holds: tanh(x)=2σ(2x)−1.

• tanh 비선형성은 오른쪽 위의 이미지에 표시됩니다.
• 실수 값을 [-1, 1] 범위로 스쿼시합니다.
• 시그모이드 뉴런과 마찬가지로 활성화는 포화되지만 시그모이드 뉴런과 달리 출력은 0을 중심으로 합니다. 따라서 실제로 tanh 비선형성은 항상 S자형 비선형성보다 선호됩니다.
• 또한 tanh 뉴런은 단순히 스케일링된 시그모이드 뉴런이며 특히 tanh(x)=2σ(2x)−1이 성립합니다.

2.3.3 Relu

ReLU. The Rectified Linear Unit has become very popular in the last few years. It computes the function f(x)=max(0,x). In other words, the activation is simply thresholded at zero (see image above on the left). There are several pros and cons to using the ReLUs:

• ReLU. Rectified Linear Unit은 지난 몇 년 동안 매우 인기를 끌었습니다.
• 함수 f(x)=max(0,x)를 계산합니다. 즉, 활성화는 단순히 0으로 임계값이 지정됩니다(왼쪽 위 이미지 참조).
• ReLU 사용에는 몇 가지 장단점이 있습니다.

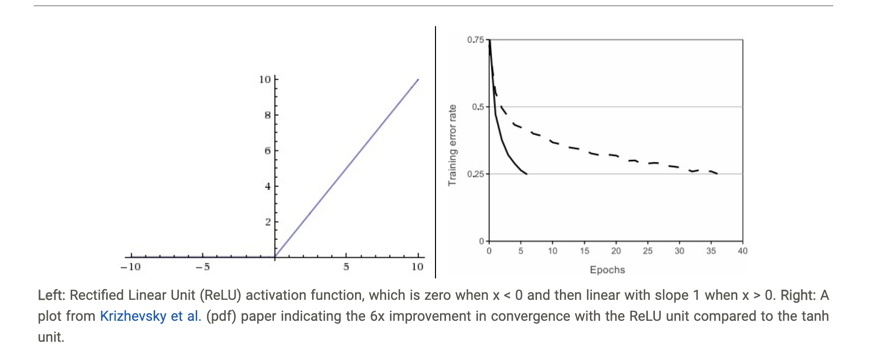
(+) It was found to greatly accelerate (e.g. a factor of 6 in Krizhevsky et al.) the convergence of stochastic gradient descent compared to the sigmoid/tanh functions. It is argued that this is due to its linear, non-saturating form.

• 시그모이드/tanh 함수와 비교하여 확률적 경사 하강의 수렴을 크게 가속화(예: Krizhevsky et al.에서 6배)하는 것으로 밝혀졌습니다.
• 이는 선형적이고 비포화적인 형태 때문이라고 주장됩니다.

(+) Compared to tanh/sigmoid neurons that involve expensive operations (exponentials, etc.), the ReLU can be implemented by simply thresholding a matrix of activations at zero.

• (+) 비용이 많이 드는 작업(지수 등)을 포함하는 tanh/sigmoid 뉴런과 비교할 때 ReLU는 단순히 활성화 매트릭스를 0으로 임계값으로 설정하여 구현할 수 있습니다.

(-) Unfortunately, ReLU units can be fragile during training and can “die”.
For example, a large gradient flowing through a ReLU neuron could cause the weights to update in such a way that the neuron will never activate on any datapoint again.
If this happens, then the gradient flowing through the unit will forever be zero from that point on.
That is, the ReLU units can irreversibly die during training since they can get knocked off the data manifold.
For example, you may find that as much as 40% of your network can be “dead” (i.e. neurons that never activate across the entire training dataset) if the learning rate is set too high.
With a proper setting of the learning rate this is less frequently an issue.

• (-) 불행하게도 ReLU 유닛은 훈련 중에 깨지기 쉽고 “죽을” 수 있습니다.
• 예를 들어, ReLU 뉴런을 통해 흐르는 큰 기울기는 뉴런이 다시는 어떤 데이터 포인트에서도 활성화되지 않는 방식으로 가중치를 업데이트할 수 있습니다.
• 이런 일이 발생하면 장치를 통해 흐르는 그래디언트는 해당 지점부터 영원히 0이 됩니다.
• 즉, ReLU 유닛은 데이터 매니폴드에서 떨어질 수 있기 때문에 훈련 중에 돌이킬 수 없게 죽을 수 있습니다.
• 예를 들어 학습 속도가 너무 높게 설정되면 네트워크의 40%가 “죽을” 수 있습니다(즉, 전체 교육 데이터 세트에서 활성화되지 않는 뉴런).
• 학습 속도를 적절하게 설정하면 문제가 덜 자주 발생합니다.

2.3.4 Leaky ReLU

Leaky ReLU. Leaky ReLUs are one attempt to fix the “dying ReLU” problem.
Instead of the function being zero when x < 0, a leaky ReLU will instead have a small positive slope (of 0.01, or so).
That is, the function computes f(x)=𝟙(x<0)(αx)+𝟙(x>=0)(x) where α is a small constant.
Some people report success with this form of activation function, but the results are not always consistent.
The slope in the negative region can also be made into a parameter of each neuron, as seen in PReLU neurons, introduced in Delving Deep into Rectifiers, by Kaiming He et al., 2015.
However, the consistency of the benefit across tasks is presently unclear.

• 새는 ReLU. Leaky ReLU는 “죽어가는 ReLU” 문제를 해결하기 위한 하나의 시도입니다.
• x < 0일 때 함수가 0이 되는 대신 새는 ReLU는 작은 양의 기울기(0.01 정도)를 갖습니다.
• 즉, 함수는 f(x)=𝟙(x<0)(αx)+𝟙(x>=0)(x)를 계산합니다. 여기서 α는 작은 상수입니다.
• 일부 사람들은 이러한 형태의 활성화 기능으로 성공했다고 보고하지만 결과가 항상 일치하는 것은 아닙니다.
• 음수 영역의 기울기는 Kaiming He et al., 2015의 Delving Deep into Rectifiers에 도입된 PReLU 뉴런에서 볼 수 있듯이 각 뉴런의 매개변수로 만들 수도 있습니다.
• 그러나 작업 전반에 걸친 이점의 일관성은 현재 불분명하다.

2.3.5 Maxout

Maxout. Other types of units have been proposed that do not have the functional form f(wTx+b) where a non-linearity is applied on the dot product between the weights and the data.
One relatively popular choice is the Maxout neuron (introduced recently by Goodfellow et al.) that generalizes the ReLU and its leaky version.
The Maxout neuron computes the function max(wT1x+b1,wT2x+b2).
Notice that both ReLU and Leaky ReLU are a special case of this form (for example, for ReLU we have w1,b1=0).
The Maxout neuron therefore enjoys all the benefits of a ReLU unit (linear regime of operation, no saturation) and does not have its drawbacks (dying ReLU).
However, unlike the ReLU neurons it doubles the number of parameters for every single neuron, leading to a high total number of parameters.

• 가중치와 데이터 사이의 내적에 비선형성이 적용되는 함수 형식 f(wTx+b)가 없는 다른 유형의 단위가 제안되었습니다.
• 상대적으로 인기 있는 선택 중 하나는 ReLU와 Leaky 버전을 일반화하는 Maxout 뉴런(최근 Goodfellow et al.에 의해 도입됨)입니다. Maxout 뉴런은 함수 max(wT1x+b1,wT2x+b2)를 계산합니다.
• ReLU와 Leaky ReLU는 모두 이 형식의 특수한 경우입니다(예: ReLU의 경우 w1,b1=0임)
• 따라서 Maxout 뉴런은 ReLU 장치의 모든 이점(선형 작동 체제, 포화 없음)을 누리고 단점(죽어가는 ReLU)이 없습니다.
• 그러나 ReLU 뉴런과 달리 모든 단일 뉴런에 대한 매개변수 수가 두 배가 되어 전체 매개변수 수가 높아집니다.

This concludes our discussion of the most common types of neurons and their activation functions. As a last comment, it is very rare to mix and match different types of neurons in the same network, even though there is no fundamental problem with doing so.

• 이것으로 가장 일반적인 유형의 뉴런과 활성화 기능에 대한 논의를 마칩니다.
• 마지막으로, 근본적인 문제가 없더라도 동일한 네트워크에서 서로 다른 유형의 뉴런을 혼합하고 일치시키는 것은 매우 드뭅니다.

TLDR: “What neuron type should I use?” Use the ReLU non-linearity, be careful with your learning rates and possibly monitor the fraction of “dead” units in a network.
If this concerns you, give Leaky ReLU or Maxout a try. Never use sigmoid.
Try tanh, but expect it to work worse than ReLU/Maxout.

• TLDR: “어떤 뉴런 유형을 사용해야 합니까?” ReLU 비선형성을 사용하고, 학습 속도에 주의하고 네트워크에서 “죽은” 단위의 비율을 모니터링할 수 있습니다.
• 이것이 걱정된다면 Leaky ReLU 또는 Maxout을 사용해 보십시오. 시그모이드를 사용하지 마십시오.
• tanh를 시도하지만 ReLU/Maxout보다 더 나쁘게 작동할 것으로 예상합니다.

3. Neural Network architectures

3.1 Layer-wise organization

Neural Networks as neurons in graphs. Neural Networks are modeled as collections of neurons that are connected in an acyclic graph.
In other words, the outputs of some neurons can become inputs to other neurons.
Cycles are not allowed since that would imply an infinite loop in the forward pass of a network.
Instead of an amorphous blobs of connected neurons, Neural Network models are often organized into distinct layers of neurons.
For regular neural networks, the most common layer type is the fully-connected layer in which neurons between two adjacent layers are fully pairwise connected, but neurons within a single layer share no connections.
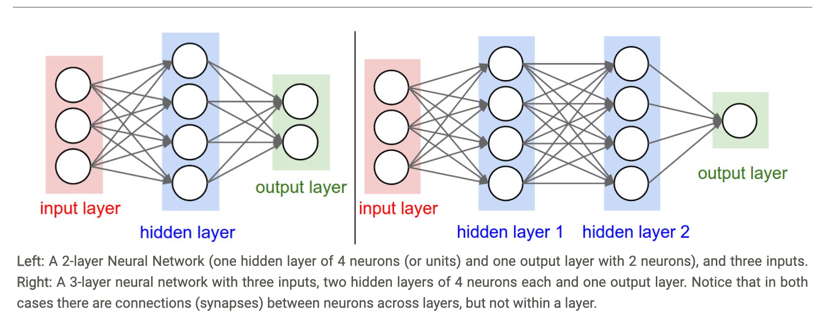
Below are two example Neural Network topologies that use a stack of fully-connected layers:

• 그래프의 뉴런으로서의 신경망. 신경망은 비순환 그래프로 연결된 뉴런 모음으로 모델링됩니다.
• 즉, 일부 뉴런의 출력이 다른 뉴런의 입력이 될 수 있습니다.
• 사이클은 네트워크의 정방향 패스에서 무한 루프를 의미하므로 허용되지 않습니다.
• 신경망 모델은 연결된 뉴런의 무정형 블롭 대신 별도의 뉴런 레이어로 구성되는 경우가 많습니다.
• 일반 신경망의 경우 가장 일반적인 계층 유형은 인접한 두 계층 사이의 뉴런이 완전히 쌍으로 연결되지만 단일 계층 내의 뉴런은 연결을 공유하지 않는 완전 연결 계층입니다.
• 다음은 완전히 연결된 계층의 스택을 사용하는 신경망 토폴로지의 두 가지 예입니다.

3.1.1 Naming conventions

Naming conventions. Notice that when we say N-layer neural network, we do not count the input layer.
Therefore, a single-layer neural network describes a network with no hidden layers (input directly mapped to output).
In that sense, you can sometimes hear people say that logistic regression or SVMs are simply a special case of single-layer Neural Networks.
You may also hear these networks interchangeably referred to as “Artificial Neural Networks” (ANN) or “Multi-Layer Perceptrons” (MLP).
Many people do not like the analogies between Neural Networks and real brains and prefer to refer to neurons as units.
-

• 명명 규칙. N 레이어 신경망을 말할 때 입력 레이어를 계산하지 않는다는 점에 유의하십시오.
• 따라서 단일 계층 신경망은 Heddin 신경망(출력에 직접 매핑된 입력)이 없는 네트워크를 설명합니다.
• 그런 의미에서 사람들이 로지스틱 회귀 또는 SVM이 단순히 단일 계층 신경망의 특수한 경우라고 말하는 것을 가끔 들을 수 있습니다. 이러한 네트워크를 “인공 신경망”(ANN) 또는 “다층 퍼셉트론”(MLP)이라고도 합니다.
• 많은 사람들은 신경망과 실제 두뇌 사이의 유추를 좋아하지 않으며 뉴런을 단위로 언급하는 것을 선호합니다.

3.1.2 Output layer.

Unlike all layers in a Neural Network, the output layer neurons most commonly do not have an activation function (or you can think of them as having a linear identity activation function).
This is because the last output layer is usually taken to represent the class scores (e.g. in classification), which are arbitrary real-valued numbers, or some kind of real-valued target (e.g. in regression).

• 신경망의 모든 레이어와 달리 출력 레이어 뉴런에는 가장 일반적으로 활성화료 함수기능이 없습니다. (또는 선형 ID 활성화 기능이 있다고 생각할 수 있음).
• 이는 마지막 출력 레이어가 일반적으로 클래스 점수(예: 분류에서)를 나타내는 데 사용되기 때문입니다. 클래스 점수는 임의의 실제 값이거나 일종의 실제 값 대상(예: 회귀)입니다.

3.1.3 Sizing neural networks

The two metrics that people commonly use to measure the size of neural networks are the number of neurons, or more commonly the number of parameters.
Working with the two example networks in the above picture:

• 사람들이 신경망의 크기를 측정하기 위해 일반적으로 사용하는 두 가지 방버은 뉴런의 수 또는 일반적으로 매개변수의 수 입니다.
• 위 그림에서 두 가지 예시 네트워크로 작업:

To give you some context, modern Convolutional Networks contain on orders of 100 million parameters and are usually made up of approximately 10-20 layers (hence deep learning).
However, as we will see the number of effective connections is significantly greater due to parameter sharing. More on this in the Convolutional Neural Networks module.

• 컨텍스트를 제공하기 위해 최신 Convolutional Networks에는 1억 개의 매개변수가 포함되어 있으며 일반적으로 약 10-20개의 레이어로 구성됩니다(따라서 딥 러닝).
• 그러나 매개변수 공유로 인해 효과적인 연결 수가 훨씬 더 많아지는 것을 보게 될 것입니다. Convolutional Neural Networks 모듈에서 이에 대해 자세히 알아보세요.

3.2 Example feed-forward computation

Repeated matrix multiplications interwoven with activation function.
One of the primary reasons that Neural Networks are organized into layers is that this structure makes it very simple and efficient to evaluate Neural Networks using matrix vector operations.
Working with the example three-layer neural network in the diagram above, the input would be a [3x1] vector.
All connection strengths for a layer can be stored in a single matrix. For example, the first hidden layer’s weights W1 would be of size [4x3], and the biases for all units would be in the vector b1, of size [4x1].
Here, every single neuron has its weights in a row of W1, so the matrix vector multiplication np.dot(W1,x) evaluates the activations of all neurons in that layer.
Similarly, W2 would be a [4x4] matrix that stores the connections of the second hidden layer, and W3 a [1x4] matrix for the last (output) layer.
The full forward pass of this 3-layer neural network is then simply three matrix multiplications, interwoven with the application of the activation function:

• 활성화 기능과 짜여진 반복 행렬 곱셈.
• 신경망이 계층으로 구성되는 주된 이유 중 하나는 이 구조가 행렬 벡터 연산을 사용하여 신경망을 평가하는 것을 매우 간단하고 효율적으로 만들기 때문입니다.
• 위의 다이어그램에서 예제 3계층 신경망으로 작업하면 입력은 [3x1] 벡터가 됩니다. 레이어의 모든 연결 강도는 단일 매트릭스에 저장할 수 있습니다.
• 예를 들어 첫 번째 히든 레이어의 가중치 W1은 크기가 [4x3]이고 모든 단위에 대한 바이어스는 크기가 [4x1]인 벡터 b1에 있습니다.
• 여기에서 모든 단일 뉴런은 W1의 행에 가중치가 있으므로 행렬 벡터 곱셈 np.dot(W1,x)는 해당 계층에 있는 모든 뉴런의 활성화를 평가합니다.
• 마찬가지로 W2는 두 번째 숨겨진 레이어의 연결을 저장하는 [4x4] 행렬이고 W3은 마지막(출력) 레이어에 대한 [1x4] 행렬입니다. 이 3계층 신경망의 전체 정방향 통과는 활성화 함수의 적용과 짜여진 3개의 행렬 곱셈입니다.

In the above code, [W1,W2,W3,b1,b2,b3] are the learnable parameters of the network.
Notice also that instead of having a single input column vector, the variable x could hold an entire batch of training data (where each input example would be a column of x) and then all examples would be efficiently evaluated in parallel.
Notice that the final Neural Network layer usually doesn’t have an activation function (e.g. it represents a (real-valued) class score in a classification setting).

• 위의 코드에서 [W1,W2,W3,b1,b2,b3]은 네트워크의 학습 가능한 매개변수입니다.
• 또한 단일 입력 열 벡터를 갖는 대신 변수 x는 훈련 데이터의 전체 배치(각 입력 예는 x의 열이 됨)를 보유할 수 있으며 모든 예는 병렬로 효율적으로 평가됩니다.
• 최종 신경망 계층에는 일반적으로 활성화 함수가 없습니다(예: 분류 설정에서 (실제 값) 클래스 점수를 나타냄).

3.3. Representational power

One way to look at Neural Networks with fully-connected layers is that they define a family of functions that are parameterized by the weights of the network.
A natural question that arises is: What is the representational power of this family of functions?
In particular, are there functions that cannot be modeled with a Neural Network?

• 완전히 연결된 계층이 있는 신경망을 보는 한 가지 방법은 신경망 가중치로 매개 변수화되는 기능군을 정의한다는 것입니다.
• 발생하는 자연스러운 질문은 다음과 같습니다. 이 기능 계열의 표현력은 무엇입니까?
• 특히 신경망으로 모델링할 수 없는 기능이 있습니까?

It turns out that Neural Networks with at least one hidden layer are universal approximators.
That is, it can be shown (e.g. see Approximation by Superpositions of Sigmoidal Function from 1989 (pdf), or this intuitive explanation from Michael Nielsen) that given any continuous function f(x) and some ϵ>0, there exists a Neural Network g(x) with one hidden layer (with a reasonable choice of non-linearity, e.g. sigmoid) such that ∀x,∣f(x)−g(x)∣<ϵ.
In other words, the neural network can approximate any continuous function.

• 적어도 하나의 숨겨진 레이어가 있는 신경망은 보편적인 근사치인 것으로 나타났습니다.
• 즉, 임의의 연속 함수 f(x)와 일부 ϵ>0이 주어지면 (예를 들어, 시그모이드 함수의 중첩에 의한 근사치 또는 마이클 닐슨의 직관적 설명 참조), ∀x, ,x와 같은 하나의 숨겨진 층(비선형성의 합리적인 선택을 가진)을 가진 신경망 g(x)가 존재한다는 것을 보여줄 수 있습니다,「f(x)-g(x)」<.
• 다시 말해, 신경망은 모든 연속 함수에 근접할 수 있습니다.

If one hidden layer suffices to approximate any function, why use more layers and go deeper?
The answer is that the fact that a two-layer Neural Network is a universal approximator is, while mathematically cute, a relatively weak and useless statement in practice.
In one dimension, the “sum of indicator bumps” function g(x)=∑ici𝟙(ai<x<bi) where a,b,c are parameter vectors is also a universal approximator,
but noone would suggest that we use this functional form in Machine Learning.
Neural Networks work well in practice because they compactly express nice, smooth functions that fit well with the statistical properties of data we encounter in practice, and are also easy to learn using our optimization algorithms (e.g. gradient descent).
Similarly, the fact that deeper networks (with multiple hidden layers) can work better than a single-hidden-layer networks is an empirical observation, despite the fact that their representational power is equal.

• 숨겨진 계층 하나로 기능을 근사화할 수 있다면 더 많은 계층을 사용하고 더 깊이 파고드는 이유는 무엇입니까?
• 답은 2층 신경망이 보편적인 근사기라는 사실은 수학적으로 귀엽지만 실제로는 상대적으로 약하고 쓸모없는 진술이라는 것입니다.
• 하나의 차원에서, a,b,c 매개변수 벡터가 보편적인 근사기이기도 하지만,
• 아무도 기계 학습에서 이 기능 형태를 사용할 것을 제안하지 않을 것입니다.
• 신경망은 실제에서 잘 작동하는데, 이는 실제에서 우리가 접하는 데이터의 통계적 특성에 잘 맞는 멋지고 매끄러운 함수를 압축적으로 표현하고 최적화 알고리듬(예: 경사 하강법)을 사용하여 학습하기 쉽기 때문입니다.
• 마찬가지로, (여러 개의 숨겨진 레이어가 있는) 심층 네트워크가 단일 은닉 레이어 네트워크보다 더 잘 작동할 수 있다는 사실은 표현력이 동일하다는 사실에도 불구하고 경험적 관찰입니다.

As an aside, in practice it is often the case that 3-layer neural networks will outperform 2-layer nets, but going even deeper (4,5,6-layer) rarely helps much more.
This is in stark contrast to Convolutional Networks, where depth has been found to be an extremely important component for a good recognition system (e.g. on order of 10 learnable layers).
One argument for this observation is that images contain hierarchical structure (e.g. faces are made up of eyes, which are made up of edges, etc.), so several layers of processing make intuitive sense for this data domain.

• 여담이지만, 실제로는 3계층 신경망이 2계층 신경망보다 성능이 좋은 경우가 많지만 더 깊은(4,5,6계층) 신경망은 훨씬 더 큰 도움이 되지 않습니다.
• 이는 우수한 인식 시스템(예: 약 10개의 학습 가능한 계층)에 대해 깊이가 매우 중요한 구성 요소인 것으로 밝혀진 Convolutional Networks와 극명한 대조를 이룹니다.
• 이 관찰에 대한 한 가지 주장은 이미지가 계층 구조(예: 얼굴은 눈으로 구성되고 가장자리로 구성됨 등)를 포함하므로 이 데이터 도메인에 대해 여러 계층의 처리가 직관적으로 이해된다는 것입니다.

The full story is, of course, much more involved and a topic of much recent research. If you are interested in these topics we recommend for further reading:

• Deep Learning book in press by Bengio, Goodfellow, Courville, in particular Chapter 6.4.
  
• Do Deep Nets Really Need to be Deep?
  
• FitNets: Hints for Thin Deep Nets
  

3.4 Setting number of layers and their sizes

How do we decide on what architecture to use when faced with a practical problem?
Should we use no hidden layers? One hidden layer? Two hidden layers?
How large should each layer be?
First, note that as we increase the size and number of layers in a Neural Network, the capacity of the network increases.
That is, the space of representable functions grows since the neurons can collaborate to express many different functions.
For example, suppose we had a binary classification problem in two dimensions.
We could train three separate neural networks, each with one hidden layer of some size and obtain the following classifiers:

• 실제 문제에 직면했을 때 사용할 아키텍처를 어떻게 결정합니까?
• 숨겨진 레이어를 사용하지 않아야 합니까? 하나의 숨겨진 레이어?
• 두 개의 히든 레이어? 각 레이어는 얼마나 커야 합니까?
• 첫째, 신경망에서 레이어의 크기와 수를 늘리면 네트워크 용량이 증가합니다.
• 즉, 뉴런이 협력하여 다양한 기능을 표현할 수 있기 때문에 표현 가능한 기능의 공간이 커집니다.
• 예를 들어 2차원에서 이진 분류 문제가 있다고 가정합니다.
• 우리는 각각 일정한 크기의 하나의 숨겨진 레이어가 있는 세 개의 개별 신경망을 훈련하고 다음 분류기를 얻을 수 있습니다.

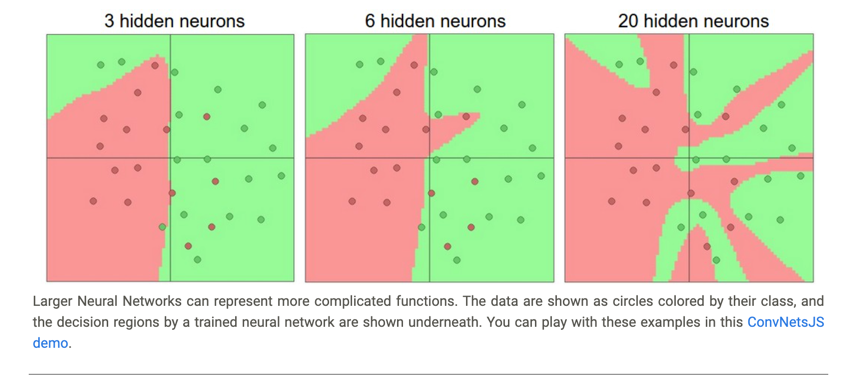
In the diagram above, we can see that Neural Networks with more neurons can express more complicated functions.
However, this is both a blessing (since we can learn to classify more complicated data) and a curse (since it is easier to overfit the training data).
Overfitting occurs when a model with high capacity fits the noise in the data instead of the (assumed) underlying relationship.
For example, the model with 20 hidden neurons fits all the training data but at the cost of segmenting the space into many disjoint red and green decision regions.
The model with 3 hidden neurons only has the representational power to classify the data in broad strokes.
It models the data as two blobs and interprets the few red points inside the green cluster as outliers (noise). In practice, this could lead to better generalization on the test set.

• 위의 다이어그램에서 우리는 더 많은 뉴런을 가진 신경망이 더 복잡한 기능을 표현할 수 있음을 알 수 있습니다.
• 그러나 이것은 축복(더 복잡한 데이터를 분류하는 방법을 배울 수 있기 때문에)인 동시에 저주(훈련 데이터를 과대적합하기 쉽기 때문에)입니다.
• 용량이 큰 모델이 (가정된) 기본 관계 대신 데이터의 노이즈를 맞출 때 과적합이 발생합니다.
• 예를 들어, 20개의 은닉 뉴런이 있는 모델은 모든 교육 데이터에 적합하지만 공간을 많은 분리된 빨간색 및 녹색 결정 영역으로 분할하는 비용이 듭니다.
• 은닉 뉴런이 3개인 모델은 데이터를 광범위하게 분류할 수 있는 표현력만 있습니다.
• 데이터를 두 개의 얼룩으로 모델링하고 녹색 클러스터 내부의 몇 가지 빨간색 점을 이상치(노이즈)로 해석합니다. 실제로 이것은 테스트 세트에서 더 나은 일반화로 이어질 수 있습니다.

Based on our discussion above, it seems that smaller neural networks can be preferred if the data is not complex enough to prevent overfitting.
However, this is incorrect - there are many other preferred ways to prevent overfitting in Neural Networks that we will discuss later (such as L2 regularization, dropout, input noise).
In practice, it is always better to use these methods to control overfitting instead of the number of neurons.

• 위의 논의를 기반으로 데이터가 과적합을 방지할 만큼 충분히 복잡하지 않은 경우 더 작은 신경망이 선호될 수 있는 것으로 보입니다.
• 그러나 이것은 잘못된 것입니다. 나중에 논의할 신경망에서 과적합을 방지하기 위해 선호되는 다른 방법(예: L2 정규화, 드롭아웃, 입력 노이즈)이 많이 있습니다.
• 실제로는 이러한 방법을 사용하여 뉴런 수 대신 과적합을 제어하는 것이 항상 더 좋습니다.

The subtle reason behind this is that smaller networks are harder to train with local methods such as Gradient Descent:
It’s clear that their loss functions have relatively few local minima, but it turns out that many of these minima are easier to converge to, and that they are bad (i.e. with high loss).
Conversely, bigger neural networks contain significantly more local minima, but these minima turn out to be much better in terms of their actual loss.
Since Neural Networks are non-convex, it is hard to study these properties mathematically, but some attempts to understand these objective functions have been made, e.g. in a recent paper The Loss Surfaces of Multilayer Networks.
In practice, what you find is that if you train a small network the final loss can display a good amount of variance - in some cases you get lucky and converge to a good place but in some cases you get trapped in one of the bad minima.
On the other hand, if you train a large network you’ll start to find many different solutions, but the variance in the final achieved loss will be much smaller. In other words, all solutions are about equally as good, and rely less on the luck of random initialization.

• 미묘한 이유는 소규모 네트워크는 경사 하강법과 같은 로컬 방법으로 훈련하기가 더 어렵다는 것입니다.
• 손실 함수의 로컬 최소값이 상대적으로 적다는 것은 분명하지만 이러한 최소값 중 많은 부분이 수렴하기 더 쉽고 그것들은 나쁘다(즉, 높은 손실).
• 반대로 더 큰 신경망은 훨씬 더 많은 로컬 최소값을 포함하지만 이러한 최소값은 실제 손실 측면에서 훨씬 더 나은 것으로 판명되었습니다.
• 신경망은 볼록하지 않기 때문에 이러한 속성을 수학적으로 연구하기는 어렵지만 이러한 목적 함수를 이해하려는 몇 가지 시도가 있었습니다.
• 최근 논문 The Loss Surfaces of Multilayer Networks에서. 실제로, 당신이 발견한 것은 작은 네트워크를 훈련시키는 경우 최종 손실이 상당한 양의 분산을 표시할 수 있다는 것입니다.
• 어떤 경우에는 운이 좋아 좋은 곳으로 수렴하지만 어떤 경우에는 나쁜 최소값 중 하나에 갇히게 됩니다.
• 반면에 대규모 네트워크를 교육하는 경우 다양한 솔루션을 찾기 시작하지만 최종 달성 손실의 분산은 훨씬 작아집니다. 즉, 모든 솔루션은 거의 동등하게 우수하며 무작위 초기화의 운에 덜 의존합니다.

To reiterate, the regularization strength is the preferred way to control the overfitting of a neural network. We can look at the results achieved by three different settings:

• 다시 말하면 정규화 강도는 신경망의 과적합을 제어하는 데 선호되는 방법입니다. 세 가지 다른 설정으로 얻은 결과를 볼 수 있습니다.

4. Summary

We introduced a very coarse model of a biological neuron.
We discussed several types of activation functions that are used in practice, with ReLU being the most common choice.
We introduced Neural Networks where neurons are connected with Fully-Connected layers where neurons in adjacent layers have full pair-wise connections, but neurons within a layer are not connected.
We saw that this layered architecture enables very efficient evaluation of Neural Networks based on matrix multiplications interwoven with the application of the activation function.
We saw that that Neural Networks are universal function approximators, but we also discussed the fact that this property has little to do with their ubiquitous use. They are used because they make certain “right” assumptions about the functional forms of functions that come up in practice.
We discussed the fact that larger networks will always work better than smaller networks, but their higher model capacity must be appropriately addressed with stronger regularization (such as higher weight decay), or they might overfit. We will see more forms of regularization (especially dropout) in later sections.

• 생물학적 뉴런의 매우 거친 모델을 도입했습니다.
• 우리는 실제로 사용되는 여러 유형의 활성화 함수에 대해 논의했으며 ReLU가 가장 일반적인 선택입니다.
• 우리는 인접한 레이어의 뉴런이 전체 쌍으로 연결되어 있지만 레이어 내의 뉴런은 연결되지 않은 완전 연결 레이어와 뉴런이 연결되는 신경망을 도입했습니다.
• 우리는 이 계층화된 아키텍처가 활성화 함수의 적용과 짜여진 행렬 곱셈을 기반으로 신경망을 매우 효율적으로 평가할 수 있음을 확인했습니다.
• 우리는 신경망이 범용 함수 근사자라는 것을 보았지만 이 속성이 유비쿼터스 사용과 거의 관련이 없다는 사실에 대해서도 논의했습니다. 그것들은 실제로 나타나는 함수의 기능적 형태에 대해 특정한 “올바른” 가정을 하기 때문에 사용됩니다.
• 우리는 더 큰 네트워크가 더 작은 네트워크보다 항상 더 잘 작동한다는 사실에 대해 논의했지만 더 큰 모델 용량은 더 강력한 정규화(예: 더 높은 가중치 감쇠)로 적절하게 해결되어야 합니다. 그렇지 않으면 과적합될 수 있습니다. 이후 섹션에서 정규화(특히 드롭아웃)의 더 많은 형태를 보게 될 것입니다.

5. Additional references

• https://cs231n.github.io