cs231n 강의 노트 7장 Neural Networks Part 3: Learning and Evaluation

Neural Networks Part 3: Learning and Evaluation 정리

Preview

Learning In the previous sections we’ve discussed the static parts of a Neural Networks: how we can set up the network connectivity, the data, and the loss function.
This section is devoted to the dynamics, or in other words, the process of learning the parameters and finding good hyperparameters.

• 학습
• 이전 섹션에서 신경망의 정적 부분인 네트워크 연결, 데이터 및 손실 함수를 설정하는 방법에 대해 논의했습니다.
• 이 섹션은 역학, 즉 매개변수를 학습하고 좋은 하이퍼 매개변수를 찾는 과정을 다룹니다.

1. Gradient checks

Gradient Checks In theory, performing a gradient check is as simple as comparing the analytic gradient to the numerical gradient.
In practice, the process is much more involved and error prone.
Here are some tips, tricks, and issues to watch out for:
Use the centered formula. The formula you may have seen for the finite difference approximation when evaluating the numerical gradient looks as follows:

• 그라디언트 검사
• 이론적으로 그래디언트 검사를 수행하는 것은 분석 그래디언트를 수치 그래디언트와 비교하는 것만큼 간단합니다.
• 실제로 프로세스는 훨씬 복잡하고 오류가 발생하기 쉽습니다.
• 다음은 주의해야 할 몇 가지 팁, 요령 및 문제입니다.
• 중심 수식을 사용합니다. 수치 기울기를 평가할 때 유한 차분 근사에 대해 보았을 수 있는 공식은 다음과 같습니다.

1.1 Use the centered formula.

The formula you may have seen for the finite difference approximation when evaluating the numerical gradient looks as follows:

\[\frac{df(x)}{dx} = \frac{f(x + h) - f(x - h)}{2h} \hspace{0.1in} \text{(use instead)}\]

• 중심 수식을 사용합니다.
• 수치 기울기를 평가할 때 유한 차분 근사에 대해 보았을 수 있는 공식은 다음과 같습니다.

where \(h\) is a very small number, in practice approximately 1e-5 or so.
In practice, it turns out that it is much better to use the centered difference formula of the form:

\[\frac{df(x)}{dx} = \frac{f(x + h) - f(x - h)}{2h} \hspace{0.1in} \text{(use instead)}\]

• 여기서 h는 매우 작은 숫자이며 실제로는 약 1e-5 정도입니다.
  
• 실제로는 다음 형식의 중심 차이 공식을 사용하는 것이 훨씬 낫다는 것이 밝혀졌습니다.
  

This requires you to evaluate the loss function twice to check every single dimension of the gradient (so it is about 2 times as expensive), but the gradient approximation turns out to be much more precise.
To see this, you can use Taylor expansion of \(f(x+h)\) and \(f(x-h)\) and verify that the first formula has an error on order of \(O(h)\), while the second formula only has error terms on order of \(O(h^2)\) (i.e. it is a second order approximation).

• 이 경우 기울기의 모든 차원을 확인하기 위해 손실 함수를 두 번 평가해야 하지만(따라서 비용이 약 2배) 기울기 근사치가 훨씬 정확한 것으로 나타났습니다.
• 이를 확인하려면 \(f(x+h)\)와 \(f(x-h)\)의 Taylor 확장을 사용하여 첫 번째 공식에 \(O(h)\), 순서의 오차가 있는지 확인하고 두 번째 공식에는 \(O(h^2)\) 순서의 오차항만 있는지 확인할 수 있습니다(즉, 2차 근사).

1.2 Use relative error for the comparison.

What are the details of comparing the numerical gradient f′n and analytic gradient f′a?
That is, how do we know if the two are not compatible?
You might be temped to keep track of the difference ∣f′a−f′n∣ or its square and define the gradient check as failed if that difference is above a threshold.

• 비교를 위해 상대 오차를 사용하십시오.
• 수치 기울기 f’n과 분석 기울기 f’a를 비교하는 세부 사항은 무엇입니까?
• 즉, 둘이 호환되지 않는지 어떻게 알 수 있습니까?
• 차이 ∣f′a−f′n∣ 또는 그 제곱을 계속 추적하고 그 차이가 임계값을 초과하면 그래디언트 검사를 실패한 것으로 정의하고 싶을 수도 있습니다.

However, this is problematic.
For example, consider the case where their difference is 1e-4.
This seems like a very appropriate difference if the two gradients are about 1.0, so we’d consider the two gradients to match.
But if the gradients were both on order of 1e-5 or lower, then we’d consider 1e-4 to be a huge difference and likely a failure.
Hence, it is always more appropriate to consider the relative error:

• 그러나 이것은 문제가 있습니다.
• 예를 들어, 차이가 1e-4인 경우를 고려하십시오.
• 이것은 두 개의 기울기가 약 1.0인 경우 매우 적절한 차이인 것처럼 보이므로 두 개의 기울기가 일치하는 것으로 간주합니다.
• 그러나 그래디언트가 모두 1e-5 이하이면 1e-4가 큰 차이로 간주되어 실패할 가능성이 높습니다.
• 따라서 상대 오류를 고려하는 것이 항상 더 적절합니다.

\[\frac{\mid f'_a - f'_n \mid}{\max(\mid f'_a \mid, \mid f'_n \mid)}\]

which considers their ratio of the differences to the ratio of the absolute values of both gradients.
Notice that normally the relative error formula only includes one of the two terms (either one), but I prefer to max (or add) both to make it symmetric and to prevent dividing by zero in the case where one of the two is zero (which can often happen, especially with ReLUs).
However, one must explicitly keep track of the case where both are zero and pass the gradient check in that edge case. In practice:

• 두 그라디언트의 절대 값 비율에 대한 차이 비율을 고려합니다.
• 일반적으로 상대 오차 공식에는 두 항 중 하나(둘 중 하나)만 포함되지만 대칭으로 만들고 둘 중 하나가 0인 경우에 0으로 나누는 것을 방지하기 위해 둘 다 최대화(또는 추가)하는 것을 선호합니다( 특히 ReLU에서 종종 발생할 수 있음).
• 그러나 둘 다 0인 경우를 명시적으로 추적하고 해당 에지 케이스에서 그래디언트 검사를 통과해야 합니다. 실제로:

relative error > 1e-2 usually means the gradient is probably wrong
1e-2 > relative error > 1e-4 should make you feel uncomfortable
1e-4 > relative error is usually okay for objectives with kinks.
But if there are no kinks (e.g. use of tanh nonlinearities and softmax), then 1e-4 is too high.
1e-7 and less you should be happy.

• 상대 오차 > 1e-2는 일반적으로 기울기가 잘못되었을 수 있음을 의미합니다
• 1e-2 > 상대적 오류 > 1e-4는 당신을 불편하게 할 것입니다
• 1e-4 > 상대 오차는 일반적으로 꺽임이 있는 목적함수에 대해 괜찮습니다.
• 그러나 꺽임(예: tanh 및 softmax 사용)이 없으면 1e-4가 너무 높습니다.
• 1e-7 이하는 행복해야 합니다.

Also keep in mind that the deeper the network, the higher the relative errors will be.
So if you are gradient checking the input data for a 10-layer network, a relative error of 1e-2 might be okay because the errors build up on the way.
Conversely, an error of 1e-2 for a single differentiable function likely indicates incorrect gradient.

• 또한 네트워크가 깊을수록 상대 오류가 높아진다는 점을 명심하십시오.
• 따라서 10계층 네트워크의 입력 데이터에 대한 그래디언트 검사를 수행하는 경우 오류가 누적되기 때문에 1e-2의 상대 오류는 괜찮을 수 있습니다.
• 반대로 단일 미분 가능 함수에 대한 1e-2 오류는 기울기가 잘못되었음을 나타냅니다.

1.3 Use double precision.

A common pitfall is using single precision floating point to compute gradient check.
It is often that case that you might get high relative errors (as high as 1e-2) even with a correct gradient implementation.
In my experience I’ve sometimes seen my relative errors plummet from 1e-2 to 1e-8 by switching to double precision.

• 배정밀도를 사용합니다. 일반적인 함정은 그래디언트 검사를 계산하기 위해 단정밀도 부동 소수점을 사용하는 것입니다.
• 올바른 그래디언트 구현으로도 높은 상대 오류(1e-2만큼 높음)를 얻을 수 있는 경우가 종종 있습니다.
• 내 경험상 나는 때때로 배정밀도로 전환함으로써 상대 오류가 1e-2에서 1e-8로 급감하는 것을 보았습니다.

1.4 Stick around active range of floating point.

It’s a good idea to read through “What Every Computer Scientist Should Know About Floating-Point Arithmetic”, as it may demystify your errors and enable you to write more careful code.
For example, in neural nets it can be common to normalize the loss function over the batch.
However, if your gradients per datapoint are very small, then additionally dividing them by the number of data points is starting to give very small numbers, which in turn will lead to more numerical issues.
This is why I like to always print the raw numerical/analytic gradient, and make sure that the numbers you are comparing are not extremely small (e.g. roughly 1e-10 and smaller in absolute value is worrying).
If they are you may want to temporarily scale your loss function up by a constant to bring them to a “nicer” range where floats are more dense - ideally on the order of 1.0, where your float exponent is 0.

• 부동 소수점의 활성 범위를 유지하십시오.
• “모든 컴퓨터 과학자가 알아야 할 부동 소수점 산술에 대해 알아야 할 사항”을 읽는 것이 좋습니다. 오류를 이해하고 보다 신중한 코드를 작성할 수 있도록 하기 때문입니다.
• 예를 들어 신경망에서는 배치에 대한 손실 함수를 정규화하는 것이 일반적일 수 있습니다.
• 그러나 데이터 포인트당 그래디언트가 매우 작은 경우 추가로 데이터 포인트 수로 나누면 매우 작은 숫자가 제공되기 시작하여 더 많은 수치 문제가 발생합니다.
• 이것이 내가 항상 원시 수치/분석 기울기를 인쇄하는 것을 좋아하고 비교하는 숫자가 너무 작지 않은지 확인하는 이유입니다(예: 대략 1e-10 이하의 절대값이 걱정됨).
• 그렇다면 손실 함수를 상수만큼 임시로 확장하여 플로트가 더 조밀한 “더 나은” 범위로 가져오는 것이 좋습니다. 이상적으로는 플로트 지수가 0인 1.0 정도입니다.

1.5 Kinks in the objective.

One source of inaccuracy to be aware of during gradient checking is the problem of kinks.
Kinks refer to non-differentiable parts of an objective function, introduced by functions such as ReLU (max(0,x)), or the SVM loss, Maxout neurons, etc. Consider gradient checking the ReLU function at x=−1e6.
Since x<0, the analytic gradient at this point is exactly zero.
However, the numerical gradient would suddenly compute a non-zero gradient because f(x+h) might cross over the kink (e.g. if h>1e−6) and introduce a non-zero contribution.
You might think that this is a pathological case, but in fact this case can be very common.
For example, an SVM for CIFAR-10 contains up to 450,000 max(0,x) terms because there are 50,000 examples and each example yields 9 terms to the objective.
Moreover, a Neural Network with an SVM classifier will contain many more kinks due to ReLUs.

• 목적 함수에서 꺽인 점. 그래디언트 검사 중에 알아야 할 부정확성의 원인 중 하나는 꺽임 문제입니다.
• 꺾임는 목적함수의 미분 불가능한 영역을 의미하며, ReLU, max(0, X), SVM loss, Maxout 뉴런 등에서 다루었습니다. 예를들어 x=−1e6에서 ReLU 함수의 그래디언트 검사를 고려하십시오.
• x<0이므로 이 지점에서의 분석 기울기는 정확히 0입니다.
• 그러나 f(x+h)가 꺽임(예: h>1e-6인 경우)을 교차하고 0이 아닌 기여를 도입할 수 있기 때문에 수치 기울기는 갑자기 0이 아닌 기울기를 계산합니다.
• 이것이 병리적인 경우라고 생각할 수도 있지만, 사실 이 경우는 매우 흔할 수 있습니다.
• 예를 들어, CIFAR-10용 SVM에는 최대 450,000개의 max(0,x) 항이 포함됩니다. 예가 50,000개 있고 각 예에서 목표에 대한 항이 9개 생성되기 때문입니다.
• 또한 SVM 분류기가 있는 신경망에는 ReLU로 인해 더 많은 꺽임이 포함됩니다.

Note that it is possible to know if a kink was crossed in the evaluation of the loss.
This can be done by keeping track of the identities of all “winners” in a function of form max(x,y);
That is, was x or y higher during the forward pass.
If the identity of at least one winner changes when evaluating f(x+h) and then f(x−h), then a kink was crossed and the numerical gradient will not be exact.

• 손실 평가에서 꺽임이 교차되었는지 여부를 알 수 있습니다.
• 이는 max(x,y) 형식의 함수에서 모든 “승자”의 신원을 추적하여 수행할 수 있습니다.
• 즉, 포워드 패스 동안 x 또는 y 더 높았습니다.
• f(x+h)를 평가한 다음 f(x-h)를 평가할 때 적어도 하나의 승자의 ID가 변경되면 꺽임이 교차되고 수치 기울기가 정확하지 않게 됩니다.

1.6 Use only few datapoints.

One fix to the above problem of kinks is to use fewer datapoints, since loss functions that contain kinks (e.g. due to use of ReLUs or margin losses etc.) will have fewer kinks with fewer datapoints, so it is less likely for you to cross one when you perform the finite different approximation.
Moreover, if your gradcheck for only 2 ~ 3 datapoints then you would almost certainly gradcheck for an entire batch.
Using very few datapoints also makes your gradient check faster and more efficient.

• 작은 수의 데이터만 사용
• 위의 꺽임 문제에 대한 한 가지 해결 방법은 꺽임을 포함하는 손실 함수(예: ReLU 사용 또는 마진 손실 등)가 더 적은 데이터 포인트로 꺽임이 적기 때문에 더 적은 데이터 포인트를 사용하는 것입니다. 유한 다른 근사를 수행할 때 하나입니다.
• 게다가 2개 ~ 3개의 데이터 포인트에 대해서만 그라데이션 검사를 수행하면 전체 배치에 대해 그라데이션 검사를 수행할 수 있습니다.
• 또한 매우 적은 수의 데이터 포인트를 사용하면 그라데이션 검사를 더 빠르고 효율적으로 수행할 수 있습니다.

1.7 Be careful with the step size h.

It is not necessarily the case that smaller is better, because when h is much smaller, you may start running into numerical precision problems.
Sometimes when the gradient doesn’t check, it is possible that you change h to be 1e-4 or 1e-6 and suddenly the gradient will be correct.
This wikipedia article contains a chart that plots the value of h on the x-axis and the numerical gradient error on the y-axis.

• 단계 크기 h에 주의하십시오.
• 작을수록 좋다는 것은 아닙니다. h가 훨씬 작을 때 수치적 정밀도 문제가 발생할 수 있기 때문입니다.
• 때때로 그래디언트가 확인되지 않을 때 h를 1e-4 또는 1e-6으로 변경하면 갑자기 그래디언트가 정확해질 수 있습니다.
• 이 wikipedia 기사에는 x축에 h 값을 표시하고 y축에 숫자 기울기 오차를 표시하는 차트가 포함되어 있습니다.

1.8 Gradcheck during a “characteristic” mode of operation.

It is important to realize that a gradient check is performed at a particular (and usually random), single point in the space of parameters.
Even if the gradient check succeeds at that point, it is not immediately certain that the gradient is correctly implemented globally.
Additionally, a random initialization might not be the most “characteristic” point in the space of parameters and may in fact introduce pathological situations where the gradient seems to be correctly implemented but isn’t.
For instance, an SVM with very small weight initialization will assign almost exactly zero scores to all datapoints and the gradients will exhibit a particular pattern across all datapoints.
An incorrect implementation of the gradient could still produce this pattern and not generalize to a more characteristic mode of operation where some scores are larger than others.
Therefore, to be safe it is best to use a short burn-in time during which the network is allowed to learn and perform the gradient check after the loss starts to go down.
The danger of performing it at the first iteration is that this could introduce pathological edge cases and mask an incorrect implementation of the gradient.

• “특성” 작동 모드 중 Gradcheck.
• 기울기 검사는 매개변수 공간의 특정(일반적으로 무작위) 단일 지점에서 수행된다는 점을 인식하는 것이 중요합니다.
• 해당 지점에서 그래디언트 검사가 성공하더라도 그래디언트가 전역적으로 올바르게 구현되는지 즉시 확신할 수 없습니다.
• 또한 무작위 초기화는 매개변수 공간에서 가장 “특징적인” 지점이 아닐 수 있으며 실제로 그래디언트가 올바르게 구현된 것처럼 보이지만 그렇지 않은 병리학적 상황을 유발할 수 있습니다.
• 예를 들어 가중치 초기화가 매우 작은 SVM은 모든 데이터 포인트에 거의 정확히 0점을 할당하고 그라디언트는 모든 데이터 포인트에서 특정 패턴을 나타냅니다.
• 그래디언트를 잘못 구현하면 여전히 이 패턴이 생성될 수 있으며 일부 점수가 다른 점수보다 큰 특징적인 작업 모드로 일반화되지 않을 수 있습니다.
• 따라서 안전을 위해 손실이 감소하기 시작한 후 네트워크가 그라디언트 검사를 학습하고 수행할 수 있는 짧은 번인 시간을 사용하는 것이 가장 좋습니다.
• 첫 번째 반복에서 이를 수행하는 것의 위험은 이것이 병리학적 에지 케이스를 도입하고 그라디언트의 잘못된 구현을 가릴 수 있다는 것입니다.

1.9 Don’t let the regularization overwhelm the data.

It is often the case that a loss function is a sum of the data loss and the regularization loss (e.g. L2 penalty on weights).
One danger to be aware of is that the regularization loss may overwhelm the data loss, in which case the gradients will be primarily coming from the regularization term (which usually has a much simpler gradient expression).
This can mask an incorrect implementation of the data loss gradient.
Therefore, it is recommended to turn off regularization and check the data loss alone first, and then the regularization term second and independently.
One way to perform the latter is to hack the code to remove the data loss contribution.
Another way is to increase the regularization strength so as to ensure that its effect is non-negligible in the gradient check, and that an incorrect implementation would be spotted.

• 정규화가 데이터를 압도하지 않도록 하십시오.
• 손실 함수가 데이터 손실과 정규화 손실의 합인 경우가 많습니다(예: 가중치에 대한 L2 페널티).
• 주의해야 할 한 가지 위험은 정규화 손실이 데이터 손실을 압도할 수 있다는 것입니다. 이 경우 그래디언트는 주로 정규화 용어(일반적으로 그래디언트 표현이 훨씬 더 간단함)에서 나옵니다.
• 이는 데이터 손실 구배의 잘못된 구현을 마스킹할 수 있습니다.
• 따라서 정규화를 끄고 데이터 손실만 먼저 확인한 다음 정규화 기간을 두 번째로 독립적으로 확인하는 것이 좋습니다.
• 후자를 수행하는 한 가지 방법은 코드를 해킹하여 데이터 손실 기여를 제거하는 것입니다.
• 또 다른 방법은 그래디언트 검사에서 그 효과가 무시할 수 없고 잘못된 구현이 발견되도록 정규화 강도를 높이는 것입니다.

1.10 Remember to turn off dropout/augmentations.

When performing gradient check, remember to turn off any non-deterministic effects in the network, such as dropout, random data augmentations, etc. Otherwise these can clearly introduce huge errors when estimating the numerical gradient.
The downside of turning off these effects is that you wouldn’t be gradient checking them (e.g. it might be that dropout isn’t backpropagated correctly).
Therefore, a better solution might be to force a particular random seed before evaluating both f(x+h) and f(x−h), and when evaluating the analytic gradient.

• 드롭아웃/증강을 끄는 것을 잊지 마십시오.
• 그래디언트 검사를 수행할 때 드롭아웃, 무작위 데이터 증가 등과 같은 네트워크의 비결정적 효과를 끄는 것을 잊지 마십시오. 그렇지 않으면 수치 그래디언트를 추정할 때 분명히 큰 오류가 발생할 수 있습니다.
• 이러한 효과를 끄는 것의 단점은 기울기를 확인하지 않는다는 것입니다(예: 드롭아웃이 올바르게 역전파되지 않을 수 있음).
• 따라서 더 나은 솔루션은 f(x+h) 및 f(x-h)를 모두 평가하기 전과 분석 기울기를 평가할 때 특정 무작위 시드를 강제하는 것일 수 있습니다.

1.11 Check only few dimensions.

In practice the gradients can have sizes of million parameters.
In these cases it is only practical to check some of the dimensions of the gradient and assume that the others are correct.
Be careful: One issue to be careful with is to make sure to gradient check a few dimensions for every separate parameter. In some applications, people combine the parameters into a single large parameter vector for convenience.
In these cases, for example, the biases could only take up a tiny number of parameters from the whole vector, so it is important to not sample at random but to take this into account and check that all parameters receive the correct gradients.

• 몇 가지 차원만 확인하십시오.
• 실제로 그래디언트는 백만 개의 매개변수 크기를 가질 수 있습니다.
• 이러한 경우 그라디언트의 차원 중 일부를 확인하고 나머지는 정확하다고 가정하는 것이 실용적입니다.
• 주의: 주의해야 할 한 가지 문제는 모든 개별 매개변수에 대해 몇 가지 치수를 그래디언트 확인해야 한다는 것입니다. 일부 응용 프로그램에서는 사람들이 편의를 위해 매개변수를 하나의 큰 매개변수 벡터로 결합합니다.
• 예를 들어 이러한 경우 편향은 전체 벡터에서 아주 적은 수의 매개변수만 사용할 수 있으므로 무작위로 샘플링하지 않고 이를 고려하여 모든 매개변수가 올바른 그래디언트를 수신하는지 확인하는 것이 중요합니다.

2. Sanity checks

Here are a few sanity checks you might consider running before you plunge into expensive optimization:

• 다음은 비용이 많이 드는 최적화에 뛰어들기 전에 실행을 고려할 수 있는 몇 가지 온전성 검사입니다.

Look for correct loss at chance performance.
Make sure you’re getting the loss you expect when you initialize with small parameters.
It’s best to first check the data loss alone (so set regularization strength to zero).
For example, for CIFAR-10 with a Softmax classifier we would expect the initial loss to be 2.302, because we expect a diffuse probability of 0.1 for each class (since there are 10 classes), and Softmax loss is the negative log probability of the correct class so: -ln(0.1) = 2.302. For The Weston Watkins SVM, we expect all desired margins to be violated (since all scores are approximately zero), and hence expect a loss of 9 (since margin is 1 for each wrong class).
If you’re not seeing these losses there might be issue with initialization.

• 우연한 성과에서 정확한 손실이 있는지 확인합니다.
• 작은 매개 변수로 초기화할 때 예상되는 손실이 발생하는지 확인합니다.
• 먼저 데이터 손실을 단독으로 확인하는 것이 가장 좋습니다(정규화 강도를 0으로 설정).
• 예를 들어, 소프트맥스 분류기가 있는 CIFAR-10의 경우 초기 손실은 2.302일 것으로 예상합니다. 왜냐하면 각 클래스에 대해 (10개의 클래스가 있기 때문에) 확산 확률이 0.1이고 소프트맥스 손실은 올바른 클래스의 음의 로그 확률입니다. 즉, -sigma(0.1) = 2.302입니다. Weston Watkins SVM의 경우 원하는 모든 마진이 위반될 것으로 예상되며(모든 점수가 약 0이기 때문에), 따라서 9의 손실이 예상됩니다(마진은 각 잘못된 클래스에 대해 1이기 때문에).
• 이러한 손실이 나타나지 않으면 초기화에 문제가 있을 수 있습니다.

As a second sanity check, increasing the regularization strength should increase the loss

• 두 번째 건전성 검사로서 정규화 강도를 높이면 손실이 증가할 것입니다 Overfit a tiny subset of data.
  Lastly and most importantly, before training on the full dataset try to train on a tiny portion (e.g. 20 examples) of your data and make sure you can achieve zero cost.
  For this experiment it’s also best to set regularization to zero, otherwise this can prevent you from getting zero cost.
  Unless you pass this sanity check with a small dataset it is not worth proceeding to the full dataset.
  Note that it may happen that you can overfit very small dataset but still have an incorrect implementation.
  For instance, if your datapoints’ features are random due to some bug, then it will be possible to overfit your small training set but you will never notice any generalization when you fold it your full dataset.
  

• 데이터의 작은 부분 집합을 오버핏합니다.
• 마지막으로, 그리고 가장 중요한 것은 전체 데이터 세트에 대한 교육을 실시하기 전에 데이터의 일부(예: 20개)에 대해 교육을 실시하여 비용을 제로로 만들 수 있는지 확인하는 것입니다.
• 이 실험의 경우 정규화를 0으로 설정하는 것이 가장 좋습니다. 그렇지 않으면 비용이 전혀 들지 않을 수 있습니다.
• 작은 데이터 세트로 이 건전성 검사를 통과하지 않는 한 전체 데이터 세트로 진행할 가치가 없습니다.
• 매우 작은 데이터 집합을 과적합할 수 있지만 잘못된 구현이 있을 수 있습니다.
• 예를 들어, 데이터 포인트의 기능이 일부 버그로 인해 무작위인 경우, 작은 훈련 세트를 과도하게 맞출 수는 있지만 전체 데이터 세트를 접을 때 일반화는 전혀 눈치채지 못합니다.

3. Babysitting the learning process

There are multiple useful quantities you should monitor during training of a neural network.
These plots are the window into the training process and should be utilized to get intuitions about different hyperparameter settings and how they should be changed for more efficient learning.

• 신경망 훈련 중에 모니터링해야 하는 여러 가지 유용한 양이 있습니다.
• 이러한 플롯은 교육 프로세스의 창이며 다양한 하이퍼파라미터 설정에 대한 직관과 보다 효율적인 학습을 위해 설정을 변경하는 방법을 파악하는 데 활용되어야 합니다.

The x-axis of the plots below are always in units of epochs, which measure how many times every example has been seen during training in expectation (e.g. one epoch means that every example has been seen once).
It is preferable to track epochs rather than iterations since the number of iterations depends on the arbitrary setting of batch size.

• 아래 플롯의 x축은 항상 에포크(epochs) 단위로, 예상 훈련 중에 모든 예제가 몇 번이나 표시되었는지 측정합니다(예: 한 에포크는 모든 예제가 한 번 표시되었음을 의미합니다).
• 반복 횟수는 배치 크기의 임의 설정에 따라 달라지므로 반복보다 에포크를 추적하는 것이 좋습니다.

3-1. Loss function

The first quantity that is useful to track during training is the loss, as it is evaluated on the individual batches during the forward pass.
Below is a cartoon diagram showing the loss over time, and especially what the shape might tell you about the learning rate:

• 교육 중에 추적하는 데 유용한 첫 번째 양은 손실입니다. 순방향 전달 중에 개별 배치에서 평가되기 때문입니다.
• 아래는 시간 경과에 따른 손실과 특히 모양이 학습률에 대해 알려주는 내용을 보여주는 만화 다이어그램입니다.

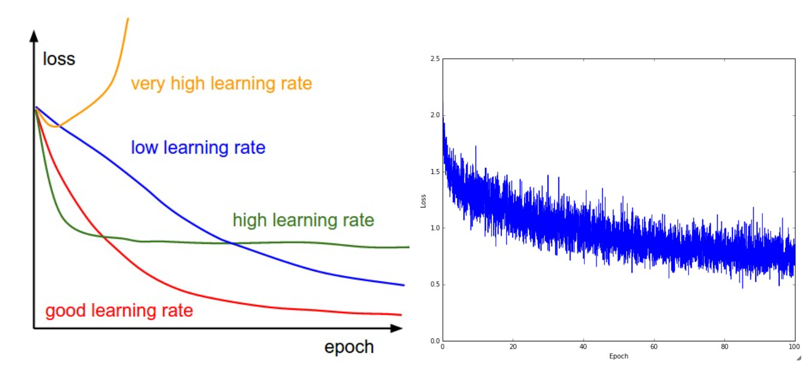
Left: A cartoon depicting the effects of different learning rates.
With low learning rates the improvements will be linear. With high learning rates they will start to look more exponential.
Higher learning rates will decay the loss faster, but they get stuck at worse values of loss (green line).
This is because there is too much “energy” in the optimization and the parameters are bouncing around chaotically, unable to settle in a nice spot in the optimization landscape.
Right: An example of a typical loss function over time, while training a small network on CIFAR-10 dataset.
This loss function looks reasonable (it might indicate a slightly too small learning rate based on its speed of decay, but it’s hard to say), and also indicates that the batch size might be a little too low (since the cost is a little too noisy).

• 왼쪽: 다양한 학습 속도의 효과를 묘사한 만화.
• 학습률이 낮으면 개선이 선형적입니다. 학습률이 높으면 더 기하급수적으로 보이기 시작할 것입니다.
• 학습 속도가 높을수록 손실이 더 빨리 감소하지만 더 나쁜 손실 값(녹색 선)에 갇히게 됩니다.
• 이는 최적화에 너무 많은 “에너지”가 있고 매개 변수가 혼란스럽게 돌아다니며 최적화 환경에서 좋은 지점에 정착할 수 없기 때문입니다.
• 오른쪽: CIFAR-10 데이터 세트에서 소규모 네트워크를 교육하는 동안 시간 경과에 따른 일반적인 손실 함수의 예입니다.
• 이 손실 함수는 합리적으로 보이며(이 함수는 붕괴 속도에 따라 학습 속도가 약간 너무 작다고 말할 수는 없지만), 배치 크기가 약간 낮을 수 있음을 나타냅니다(비용이 너무 많이 들기 때문에).

The amount of “wiggle” in the loss is related to the batch size.
When the batch size is 1, the wiggle will be relatively high.
When the batch size is the full dataset, the wiggle will be minimal because every gradient update should be improving the loss function monotonically (unless the learning rate is set too high).

• 손실의 “흔들림” 정도는 배치 크기와 관련이 있습니다.
• 배치 크기가 1이면 흔들림이 상대적으로 높아집니다.
• 배치 크기가 전체 데이터 세트인 경우 기울기 업데이트가 손실 함수를 단조롭게 개선해야 하기 때문에 흔들림이 최소화됩니다(학습 속도가 너무 높게 설정되지 않은 경우).

Some people prefer to plot their loss functions in the log domain.
Since learning progress generally takes an exponential form shape, the plot appears as a slightly more interpretable straight line, rather than a hockey stick.
Additionally, if multiple cross-validated models are plotted on the same loss graph, the differences between them become more apparent.

• 어떤 사람들은 손실 함수를 로그 도메인에 표시하는 것을 선호합니다.
• 학습 진행은 일반적으로 지수 형태를 취하기 때문에 플롯은 하키 스틱이 아니라 약간 더 해석하기 쉬운 직선으로 나타납니다.
• 또한 교차 검증된 여러 모델을 동일한 손실 그래프에 표시하면 모델 간의 차이가 더욱 분명해집니다.

Sometimes loss functions can look funny lossfunctions.tumblr.com.

• 때때로 손실 함수는 재미있어 보일 수 있습니다. lossfunctions.tumblr.com.
  

3-2 Train/val accuracy

The second important quantity to track while training a classifier is the validation/training accuracy.
This plot can give you valuable insights into the amount of overfitting in your model:

• 분류기를 교육하는 동안 추적해야 할 두 번째 중요한 수량은 유효성 검사/교육 정확도입니다.
• 이 플롯은 모델의 과적합 양에 대한 귀중한 통찰력을 제공할 수 있습니다.

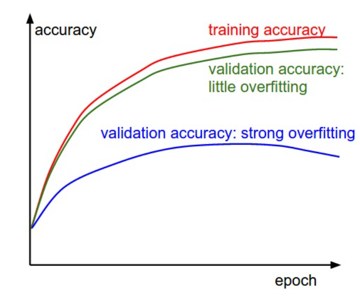
The gap between the training and validation accuracy indicates the amount of overfitting.
Two possible cases are shown in the diagram on the left. The blue validation error curve shows very small validation accuracy compared to the training accuracy, indicating strong overfitting (note, it’s possible for the validation accuracy to even start to go down after some point).
When you see this in practice you probably want to increase regularization (stronger L2 weight penalty, more dropout, etc.) or collect more data.
The other possible case is when the validation accuracy tracks the training accuracy fairly well.
This case indicates that your model capacity is not high enough: make the model larger by increasing the number of parameters.

• 훈련 정확도와 검증 정확도 사이의 차이는 과적합의 양을 나타냅니다.
• 두 가지 가능한 경우가 왼쪽 다이어그램에 나와 있습니다. 파란색 유효성 검사 오류 곡선은 훈련 정확도에 비해 매우 작은 유효성 검사 정확도를 보여 과대적합이 강함을 나타냅니다(참고: 유효성 검사 정확도가 어느 시점 이후에 떨어지기 시작할 수도 있음).
• 실제로 이것을 보면 정규화를 늘리거나(L2 가중치 페널티 강화, 드롭아웃 증가 등) 더 많은 데이터를 수집하고 싶을 것입니다.
• 다른 가능한 경우는 검증 정확도가 훈련 정확도를 상당히 잘 추적하는 경우입니다.
• 이 사례는 모델 용량이 충분히 높지 않음을 나타냅니다. 매개변수 수를 늘려 모델을 더 크게 만듭니다.

3-3. Weights:Updates ratio

The last quantity you might want to track is the ratio of the update magnitudes to the value magnitudes.
Note: updates, not the raw gradients (e.g. in vanilla sgd this would be the gradient multiplied by the learning rate).
You might want to evaluate and track this ratio for every set of parameters independently.
A rough heuristic is that this ratio should be somewhere around 1e-3.
If it is lower than this then the learning rate might be too low.
If it is higher then the learning rate is likely too high.
Here is a specific example:

• 추적할 수 있는 마지막 값은 크기에 대한 업데이트 크기의 비율입니다.
• 참고: 원시 그래디언트가 아닌 업데이트입니다(예: 바닐라 sgd에서는 그래디언트에 학습률을 곱한 값임).
• 모든 매개변수 집합에 대해 독립적으로 이 비율을 평가하고 추적할 수 있습니다.
• 대략적인 휴리스틱은 이 비율이 1e-3 정도여야 한다는 것입니다.
• 이보다 낮으면 학습률이 너무 낮을 수 있습니다.
• 더 높으면 학습률이 너무 높을 가능성이 높습니다.
• 구체적인 예는 다음과 같습니다.

# assume parameter vector W and its gradient vector dW
param_scale = np.linalg.norm(W.ravel())
update = -learning_rate*dW # simple SGD update
update_scale = np.linalg.norm(update.ravel())
W += update # the actual update
print update_scale / param_scale # want ~1e-3

Instead of tracking the min or the max, some people prefer to compute and track the norm of the gradients and their updates instead.
These metrics are usually correlated and often give approximately the same results.

• 최소값 또는 최대값을 추적하는 대신 일부 사람들은 기울기의 표준과 업데이트를 대신 계산하고 추적하는 것을 선호합니다.
• 이러한 메트릭은 일반적으로 상관 관계가 있으며 종종 거의 동일한 결과를 제공합니다.

3-4.Activation/Gradient distributions per layer

An incorrect initialization can slow down or even completely stall the learning process.
Luckily, this issue can be diagnosed relatively easily.
One way to do so is to plot activation/gradient histograms for all layers of the network.
Intuitively, it is not a good sign to see any strange distributions - e.g.
with tanh neurons we would like to see a distribution of neuron activations between the full range of [-1,1], instead of seeing all neurons outputting zero, or all neurons being completely saturated at either -1 or 1.

• 초기화가 잘못되면 학습 프로세스가 느려지거나 완전히 중단될 수 있습니다.
• 다행히 이 문제는 비교적 쉽게 진단할 수 있습니다.
• 그렇게 하는 한 가지 방법은 네트워크의 모든 계층에 대한 활성화/기울기 히스토그램을 그리는 것입니다.
• 직관적으로 이상한 분포를 보는 것은 좋은 징조가 아닙니다.
• tanh 뉴런을 사용하여 모든 뉴런이 0을 출력하거나 모든 뉴런이 -1 또는 1에서 완전히 포화되는 것을 보는 대신 [-1,1]의 전체 범위 사이에서 뉴런 활성화 분포를 보고 싶습니다.

3-5.Visualization

Lastly, when one is working with image pixels it can be helpful and satisfying to plot the first-layer features visually:

• 마지막으로 이미지 픽셀로 작업할 때 첫 번째 레이어 기능을 시각적으로 표시하는 것이 유용하고 만족스러울 수 있습니다.

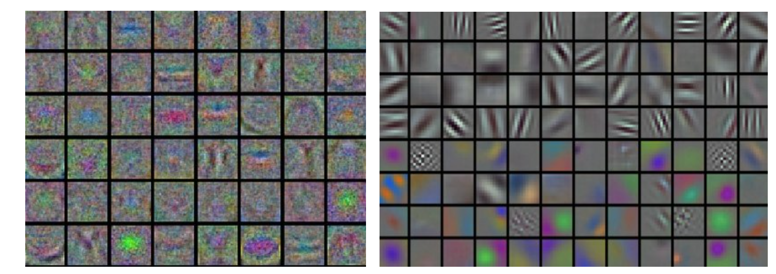
Examples of visualized weights for the first layer of a neural network.
Left: Noisy features indicate could be a symptom: Unconverged network, improperly set learning rate, very low weight regularization penalty.
Right: Nice, smooth, clean and diverse features are a good indication that the training is proceeding well.

• 신경망의 첫 번째 계층에 대한 시각화된 가중치의 예입니다.
• 왼쪽: 잡음이 있는 기능은 증상일 수 있음을 나타냅니다. 수렴되지 않은 네트워크, 부적절하게 설정된 학습 속도, 매우 낮은 가중치 정규화 페널티.
• 오른쪽: 멋지고 매끄럽고 깨끗하고 다양한 기능은 훈련이 잘 진행되고 있다는 좋은 지표입니다.

4. Parameter updates

Once the analytic gradient is computed with backpropagation, the gradients are used to perform a parameter update.
There are several approaches for performing the update, which we discuss next.

• 분석 기울기가 역전파로 계산되면 기울기는 매개변수 업데이트를 수행하는 데 사용됩니다.
• 업데이트를 수행하는 방법에는 여러 가지가 있으며, 이에 대해서는 다음에 설명합니다.

We note that optimization for deep networks is currently a very active area of research.
In this section we highlight some established and common techniques you may see in practice, briefly describe their intuition, but leave a detailed analysis outside of the scope of the class.
We provide some further pointers for an interested reader.

• 딥 네트워크를 위한 최적화는 현재 매우 활발한 연구 분야입니다.
• 이 섹션에서는 실제로 볼 수 있는 몇 가지 확립되고 일반적인 기술을 강조하고 직감을 간략하게 설명하지만 자세한 분석은 클래스 범위를 벗어납니다.
• 관심 있는 독자를 위해 몇 가지 추가 정보를 제공합니다.

4-1. First-order (SGD), momentum, Nesterov momentum

Vanilla update.
The simplest form of update is to change the parameters along the negative gradient direction (since the gradient indicates the direction of increase, but we usually wish to minimize a loss function).
Assuming a vector of parameters x and the gradient dx, the simplest update has the form:

• 바닐라 업데이트.
• 업데이트의 가장 간단한 형태는 음의 기울기 방향을 따라 매개변수를 변경하는 것입니다(기울기는 증가 방향을 나타내지만 일반적으로 손실 함수를 최소화하기를 원하기 때문입니다).
• 매개변수 x와 그래디언트 dx의 벡터를 가정하면 가장 간단한 업데이트 형식은 다음과 같습니다.

# Vanilla update
x += - learning_rate * dx

where learning_rate is a hyperparameter - a fixed constant.
When evaluated on the full dataset, and when the learning rate is low enough, this is guaranteed to make non-negative progress on the loss function.

• 여기서 learning_rate는 고정 상수인 하이퍼파라미터입니다.
• 전체 데이터 세트에서 평가하고 학습률이 충분히 낮을 때 손실 함수에서 음수가 아닌 진행이 보장됩니다.

Momentum update is another approach that almost always enjoys better converge rates on deep networks.
This update can be motivated from a physical perspective of the optimization problem.
In particular, the loss can be interpreted as the height of a hilly terrain (and therefore also to the potential energy since U=mgh and therefore U∝h ).
Initializing the parameters with random numbers is equivalent to setting a particle with zero initial velocity at some location.
The optimization process can then be seen as equivalent to the process of simulating the parameter vector (i.e. a particle) as rolling on the landscape.

• 모멘텀 업데이트는 거의 항상 심층 네트워크에서 더 나은 수렴 속도를 누리는 또 다른 접근 방식입니다.
• 이 업데이트는 최적화 문제의 물리적 관점에서 동기를 부여할 수 있습니다.
• 특히, 손실은 언덕이 많은 지형의 높이로 해석될 수 있습니다(따라서 U=mgh 및 U∝h이므로 위치 에너지로도 해석할 수 있습니다).
• 난수로 매개변수를 초기화하는 것은 어떤 위치에서 초기 속도가 0인 입자를 설정하는 것과 같습니다.
• 그런 다음 최적화 프로세스는 매개변수 벡터(즉, 입자)를 풍경에서 굴러가는 것으로 시뮬레이션하는 프로세스와 동일하게 볼 수 있습니다.

Since the force on the particle is related to the gradient of potential energy (i.e. F=−∇U ), the force felt by the particle is precisely the(negative) gradient of the loss function.
Moreover, F=ma so the (negative) gradient is in this view proportional to the acceleration of the particle.
Note that this is different from the SGD update shown above, where the gradient directly integrates the position.
Instead, the physics view suggests an update in which the gradient only directly influences the velocity, which in turn has an effect on the position:

• 입자에 가해지는 힘은 위치 에너지의 구배(즉, F=−∇U)와 관련이 있기 때문에 입자가 느끼는 힘은 정확히 손실 함수의 (음의) 구배입니다.
• 더욱이, F=ma이므로 (음의) 구배는 이 관점에서 입자의 가속도에 비례합니다.
• 이것은 그라디언트가 위치를 직접 통합하는 위에 표시된 SGD 업데이트와 다릅니다.
• 대신, 물리 보기는 그래디언트가 속도에만 직접적으로 영향을 미치고 위치에 영향을 미치는 업데이트를 제안합니다.

# Momentum update
v = mu * v - learning_rate * dx # integrate velocity
x += v # integrate position

Here we see an introduction of a v variable that is initialized at zero, and an additional hyperparameter (mu).
As an unfortunate misnomer, this variable is in optimization referred to as momentum (its typical value is about 0.9), but its physical meaning is more consistent with the coefficient of friction.
Effectively, this variable damps the velocity and reduces the kinetic energy of the system, or otherwise the particle would never come to a stop at the bottom of a hill.
When cross-validated, this parameter is usually set to values such as [0.5, 0.9, 0.95, 0.99].
Similar to annealing schedules for learning rates (discussed later, below), optimization can sometimes benefit a little from momentum schedules, where the momentum is increased in later stages of learning.
A typical setting is to start with momentum of about 0.5 and anneal it to 0.99 or so over multiple epochs.

• 여기서 우리는 0에서 초기화되는 ‘v’ 변수의 도입과 추가적인 하이퍼 파라미터(‘mu’)를 볼 수 있습니다.
• 유감스럽게도 이 변수는 모멘트(일반적인 값은 약 0.9)로 불리는 최적화 상태이지만 물리적 의미는 마찰 계수와 더 일치합니다.
• 효과적으로, 이 변수는 속도를 감소시키고 계의 운동 에너지를 감소시킵니다. 그렇지 않으면 입자는 언덕 바닥에서 절대 멈추지 않을 것입니다.
• 교차 검증된 경우 이 매개 변수는 일반적으로 [0.5, 0.9, 0.95, 0.99]와 같은 값으로 설정됩니다.
• 학습 속도에 대한 어닐링 일정(후술, 아래 설명)과 유사하게, 최적화는 때때로 학습의 후반 단계에서 모멘텀이 증가하는 모멘텀 일정으로부터 약간의 이익을 얻을 수 있습니다.
• 일반적인 설정은 약 0.5의 운동량으로 시작하여 여러 시간에 걸쳐 0.99 정도로 어닐링하는 것입니다.

With Momentum update, the parameter vector will build up velocity in any direction that has consistent gradient.

• 모멘텀 업데이트를 통해 매개변수 벡터는 일정한 기울기가 있는 모든 방향으로 속도를 증가시킵니다.

Nesterov Momentum is a slightly different version of the momentum update that has recently been gaining popularity.
It enjoys stronger theoretical converge guarantees for convex functions and in practice it also consistenly works slightly better than standard momentum.

• Nesterov Momentum은 최근 인기를 얻고 있는 모멘텀 업데이트의 약간 다른 버전입니다.
• 그것은 볼록 함수에 대한 더 강력한 이론적 수렴 보장을 누리고 있으며 실제로는 표준 운동량보다 약간 더 일관되게 작동합니다.

The core idea behind Nesterov momentum is that when the current parameter vector is at some position x, then looking at the momentum update above, we know that the momentum term alone (i.e. ignoring the second term with the gradient) is about to nudge the parameter vector by mu * v.
Therefore, if we are about to compute the gradient, we can treat the future approximate position x + mu * v as a “lookahead” - this is a point in the vicinity of where we are soon going to end up.
Hence, it makes sense to compute the gradient at x + mu * v instead of at the “old/stale” position x.

• 네스테로프 운동량의 핵심 아이디어는 현재 매개 변수 벡터가 어떤 위치 x에 있을 때 위의 운동량 업데이트를 보면 운동량 항만(즉, 기울기로 두 번째 항을 무시함)이 매개 변수 벡터를 mu * v만큼 누르기 직전이라는 것을 알고 있습니다.
• 그러므로, 우리가 기울기를 계산하려고 한다면, 우리는 미래의 대략적인 위치 x + mu * v를 “전망 전방”으로 취급할 수 있습니다. 이것은 우리가 곧 끝날 지점 근처의 지점입니다.
• 따라서 “오래된/오래된” 위치 x가 아닌 x + mu * v에서 구배를 계산하는 것이 타당합니다.

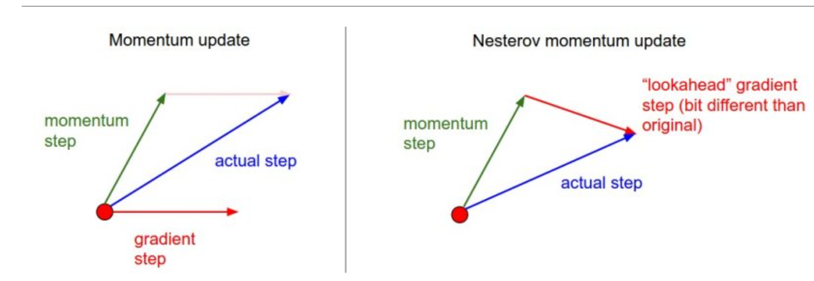
Nesterov momentum.
Instead of evaluating gradient at the current position (red circle), we know that our momentum is about to carry us to the tip of the green arrow.
With Nesterov momentum we therefore instead evaluate the gradient at this “looked-ahead” position.

• Nesterov 운동량.
• 현재 위치(빨간색 원)에서 기울기를 평가하는 대신 모멘텀이 녹색 화살표의 끝으로 이동하려고 한다는 것을 알고 있습니다.
• 따라서 Nesterov 모멘텀을 사용하여 대신 이 “예측” 위치에서 기울기를 평가합니다.

That is, in a slightly awkward notation, we would like to do the following:

• 즉, 약간 어색한 표기법으로 다음을 수행하려고 합니다.

x_ahead = x + mu * v
# evaluate dx_ahead (the gradient at x_ahead instead of at x)
v = mu * v - learning_rate * dx_ahead
x += v

However, in practice people prefer to express the update to look as similar to vanilla SGD or to the previous momentum update as possible.
This is possible to achieve by manipulating the update above with a variable transform x_ahead = x + mu * v, and then expressing the update in terms of x_ahead instead of x.
That is, the parameter vector we are actually storing is always the ahead version.
The equations in terms of x_ahead ㅁ(but renaming it back to x) then become:

• 그러나 실제로 사람들은 바닐라 SGD 또는 이전 모멘텀 업데이트와 유사하게 보이도록 업데이트를 표현하는 것을 선호합니다.
• 이는 변수 변환 x_ahead = x + mu * v로 위의 업데이트를 조작한 다음 x 대신 x_ahead로 업데이트를 표현하여 달성할 수 있습니다.
• 즉, 실제로 저장하는 매개변수 벡터는 항상 상위 버전입니다.
• x_ahead ㅁ(단, 다시 x로 이름을 바꾸면)의 방정식은 다음과 같이 됩니다.

v_prev = v # back this up
v = mu * v - learning_rate * dx # velocity update stays the same
x += -mu * v_prev + (1 + mu) * v # position update changes form

We recommend this further reading to understand the source of these equations and the mathematical formulation of Nesterov’s Accelerated Momentum (NAG):

• 이러한 방정식의 출처와 Nesterov의 가속 모멘텀(NAG)의 수학적 공식을 이해하려면 이 추가 자료를 권장합니다.

Advances in optimizing Recurrent Networks by Yoshua Bengio, Section 3.5.
Ilya Sutskever’s thesis (pdf) contains a longer exposition of the topic in section 7.2

4-2. Annealing the learning rate

In training deep networks, it is usually helpful to anneal the learning rate over time.
Good intuition to have in mind is that with a high learning rate, the system contains too much kinetic energy and the parameter vector bounces around chaotically, unable to settle down into deeper, but narrower parts of the loss function.
Knowing when to decay the learning rate can be tricky: Decay it slowly and you’ll be wasting computation bouncing around chaotically with little improvement for a long time.
But decay it too aggressively and the system will cool too quickly, unable to reach the best position it can.
There are three common types of implementing the learning rate decay:

• 심층 신경망을 훈련할 때 일반적으로 시간이 지남에 따라 학습 속도를 어닐링하는 것이 도움이 됩니다.
• 학습률이 높으면 시스템에 너무 많은 운동 에너지가 포함되고 매개변수 벡터가 혼란스럽게 돌아다니며 손실 함수의 더 깊지만 더 좁은 부분으로 정착할 수 없다는 점을 염두에 두어야 합니다.
• 학습 속도를 언제 감소시켜야 하는지 아는 것은 까다로울 수 있습니다. 천천히 감소하면 오랜 시간 동안 거의 개선되지 않고 혼란스럽게 돌아다니며 계산을 낭비하게 될 것입니다.
• 그러나 너무 공격적으로 분해하면 시스템이 너무 빨리 냉각되어 최상의 위치에 도달할 수 없습니다.
• 학습률 감소를 구현하는 세 가지 일반적인 유형이 있습니다.

Step decay: Reduce the learning rate by some factor every few epochs.
Typical values might be reducing the learning rate by a half every 5 epochs, or by 0.1 every 20 epochs.
These numbers depend heavily on the type of problem and the model.
One heuristic you may see in practice is to watch the validation error while training with a fixed learning rate, and reduce the learning rate by a constant (e.g. 0.5) whenever the validation error stops improving.

• 단계 감소: 몇 에포크마다 학습률을 일부 요소만큼 줄입니다.
• 일반적인 값은 학습 속도를 5 epoch마다 절반으로 또는 20 epoch마다 0.1씩 줄이는 것입니다.
• 이 숫자는 문제 유형과 모델에 따라 크게 달라집니다.
• 실제로 볼 수 있는 한 가지 휴리스틱은 고정된 학습 속도로 훈련하는 동안 검증 오류를 관찰하고 검증 오류가 개선되지 않을 때마다 학습 속도를 상수(예: 0.5)로 줄이는 것입니다.

Exponential decay. has the mathematical form α=α0e−kt, where α0,k are hyperparameters and t is the iteration number (but you can also use units of epochs).

• 지수적 붕괴. 수학 형식은 α=α0e−kt입니다. 여기서 α0,k는 하이퍼파라미터이고 t는 반복 횟수입니다(단, 에포크 단위를 사용할 수도 있음).

1/t decay has the mathematical form α=α0/(1+kt) where a0,k are hyperparameters and t is the iteration number.

• 1/t 붕괴의 수학 형식은 α=α0/(1+kt)입니다. 여기서 a0,k는 하이퍼파라미터이고 t는 반복 횟수입니다.

4-3. Second-order methods

A second, popular group of methods for optimization in context of deep learning is based on Newton’s method, which iterates the following update:

• 딥 러닝 맥락에서 최적화를 위한 두 번째 인기 있는 방법 그룹은 다음 업데이트를 반복하는 Newton의 방법을 기반으로 합니다.

\[x \leftarrow x - [H f(x)]^{-1} \nabla f(x)\]

Here, Hf(x) is the Hessian matrix, which is a square matrix of second-order partial derivatives of the function.
The term ∇f(x) is the gradient vector, as seen in Gradient Descent.
Intuitively, the Hessian describes the local curvature of the loss function, which allows us to perform a more efficient update.
In particular, multiplying by the inverse Hessian leads the optimization to take more aggressive steps in directions of shallow curvature and shorter steps in directions of steep curvature.
Note, crucially, the absence of any learning rate hyperparameters in the update formula, which the proponents of these methods cite this as a large advantage over first-order methods.

• 여기서 Hf(x)는 함수의 2차 편도함수의 정사각 행렬인 헤시안 행렬입니다.
• ∇f(x) 항은 기울기 하강법에서 볼 수 있는 기울기 벡터입니다.
• 직관적으로 Hessian은 손실 함수의 로컬 곡률을 설명하므로 보다 효율적인 업데이트를 수행할 수 있습니다.
• 특히, 역 헤세 행렬을 곱하면 최적화가 얕은 곡률 방향에서는 보다 공격적인 단계를 취하고 가파른 곡률 방향에서는 더 짧은 단계를 수행하도록 합니다.
• 결정적으로 업데이트 공식에 학습률 하이퍼파라미터가 없다는 점에 유의하십시오. 이러한 방법의 지지자들은 이를 1차 방법에 비해 큰 이점으로 인용합니다.

However, the update above is impractical for most deep learning applications because computing (and inverting) the Hessian in its explicit form is a very costly process in both space and time.
For instance, a Neural Network with one million parameters would have a Hessian matrix of size [1,000,000 x 1,000,000], occupying approximately 3725 gigabytes of RAM.
Hence, a large variety of quasi-Newton methods have been developed that seek to approximate the inverse Hessian.
Among these, the most popular is L-BFGS, which uses the information in the gradients over time to form the approximation implicitly (i.e. the full matrix is never computed).

• 그러나 위의 업데이트는 명시적 형식의 Hessian을 계산(및 반전)하는 것이 시간과 공간 모두에서 매우 비용이 많이 드는 프로세스이기 때문에 대부분의 딥 러닝 응용 프로그램에는 비실용적입니다.
• 예를 들어, 백만 개의 매개변수가 있는 신경망은 [1,000,000 x 1,000,000] 크기의 Hessian 행렬을 가지며 약 3725GB의 RAM을 차지합니다.
• 따라서 역헤세 행렬을 근사화하려는 다양한 준뉴턴 방법이 개발되었습니다.
• 이 중에서 가장 인기 있는 것은 L-BFGS로, 시간 경과에 따른 기울기 정보를 사용하여 암시적으로 근사를 형성합니다(즉, 전체 행렬이 계산되지 않음).

However, even after we eliminate the memory concerns, a large downside of a naive application of L-BFGS is that it must be computed over the entire training set, which could contain millions of examples.
Unlike mini-batch SGD, getting L-BFGS to work on mini-batches is more tricky and an active area of research.

• 그러나 메모리 문제를 제거한 후에도 L-BFGS의 순진한 적용의 큰 단점은 수백만 개의 예제를 포함할 수 있는 전체 훈련 세트에 대해 계산해야 한다는 것입니다.
• 미니 배치 SGD와 달리 L-BFGS가 미니 배치에서 작동하도록 하는 것은 더 까다롭고 활발한 연구 영역입니다.

In practice, it is currently not common to see L-BFGS or similar second-order methods applied to large-scale Deep Learning and Convolutional Neural Networks.
Instead, SGD variants based on (Nesterov’s) momentum are more standard because they are simpler and scale more easily.

• 실제로 L-BFGS 또는 이와 유사한 2차 방법이 대규모 딥 러닝 및 컨볼루션 신경망에 적용되는 것은 현재 일반적이지 않습니다.
• 대신, (Nesterov의) 모멘텀을 기반으로 하는 SGD 변형은 더 단순하고 더 쉽게 확장할 수 있기 때문에 더 표준입니다.

Additional references:
Large Scale Distributed Deep Networks is a paper from the Google Brain team, comparing L-BFGS and SGD variants in large-scale distributed optimization.
SFO algorithm strives to combine the advantages of SGD with advantages of L-BFGS.

4-4. Per-parameter adaptive learning rates (Adagrad, RMSProp)

All previous approaches we’ve discussed so far manipulated the learning rate globally and equally for all parameters.
Tuning the learning rates is an expensive process, so much work has gone into devising methods that can adaptively tune the learning rates, and even do so per parameter.
Many of these methods may still require other hyperparameter settings, but the argument is that they are well-behaved for a broader range of hyperparameter values than the raw learning rate.
In this section we highlight some common adaptive methods you may encounter in practice:

• 지금까지 논의한 이전의 모든 접근 방식은 모든 매개 변수에 대해 학습 속도를 전역적으로 동일하게 조작했습니다.
• 학습 속도를 조정하는 것은 비용이 많이 드는 프로세스이므로 학습 속도를 적응적으로 조정할 수 있는 방법을 고안하는 데 많은 노력을 기울였으며 심지어 매개변수별로 그렇게 할 수도 있습니다.
• 이러한 방법 중 다수는 여전히 다른 하이퍼파라미터 설정이 필요할 수 있지만 원시 학습률보다 더 넓은 범위의 하이퍼파라미터 값에 대해 잘 작동한다는 주장이 있습니다.
• 이 섹션에서는 실제로 접할 수 있는 몇 가지 일반적인 적응 방법을 강조합니다.

Adagrad is an adaptive learning rate method originally proposed by Duchi et al..

• Adagrad는 원래 Duchi et al.이 제안한 적응형 학습률 방법입니다.

  # Assume the gradient dx and parameter vector x
  cache += dx**2
  x += - learning_rate * dx / (np.sqrt(cache) + eps)
  

  Notice that the variable cache has size equal to the size of the gradient, and keeps track of per-parameter sum of squared gradients.
  This is then used to normalize the parameter update step, element-wise.
  Notice that the weights that receive high gradients will have their effective learning rate reduced, while weights that receive small or infrequent updates will have their effective learning rate increased.
  Amusingly, the square root operation turns out to be very important and without it the algorithm performs much worse.
  The smoothing term eps (usually set somewhere in range from 1e-4 to 1e-8) avoids division by zero.
  A downside of Adagrad is that in case of Deep Learning, the monotonic learning rate usually proves too aggressive and stops learning too early.
  

• 변수 캐시의 크기는 그래디언트 크기와 동일하며 매개변수별 그래디언트 제곱합을 추적합니다.
• 그런 다음 매개변수 업데이트 단계를 요소별로 정규화하는 데 사용됩니다.
• 높은 그래디언트를 받는 가중치는 유효 학습률이 감소하는 반면 작거나 드물게 업데이트되는 가중치는 유효 학습률이 증가합니다.
• 흥미롭게도 제곱근 연산은 매우 중요한 것으로 판명되었으며 이것이 없으면 알고리즘 성능이 훨씬 저하됩니다.
• 평활화 항 eps(일반적으로 1e-4에서 1e-8 사이의 범위에 설정됨)는 0으로 나누는 것을 방지합니다.
• Adagrad의 단점은 딥 러닝의 경우 일반적으로 단조로운 학습 속도가 너무 공격적이며 너무 일찍 학습을 중단한다는 것입니다.

RMSprop. RMSprop is a very effective, but currently unpublished adaptive learning rate method.
Amusingly, everyone who uses this method in their work currently cites slide 29 of Lecture 6 of Geoff Hinton’s Coursera class.
The RMSProp update adjusts the Adagrad method in a very simple way in an attempt to reduce its aggressive, monotonically decreasing learning rate.
In particular, it uses a moving average of squared gradients instead, giving:

• RMSprop. RMSprop은 매우 효과적이지만 현재 게시되지 않은 적응 학습 속도 방법입니다.
• 흥미롭게도 작업에서 이 방법을 사용하는 모든 사람들은 현재 Geoff Hinton의 Coursera 수업 강의 6의 슬라이드 29를 인용합니다.
• RMSProp 업데이트는 공격적이고 단조롭게 감소하는 학습 속도를 줄이기 위해 매우 간단한 방법으로 Adagrad 방법을 조정합니다.
• 특히 제곱 기울기의 이동 평균을 대신 사용하여 다음을 제공합니다.

cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

Here, decay_rate is a hyperparameter and typical values are [0.9, 0.99, 0.999].
Notice that the x+= update is identical to Adagrad, but the cache variable is a “leaky”.
Hence, RMSProp still modulates the learning rate of each weight based on the magnitudes of its gradients, which has a beneficial equalizing effect, but unlike Adagrad the updates do not get monotonically smaller.

• 여기서 Decay_rate는 하이퍼파라미터이며 일반적인 값은 [0.9, 0.99, 0.999]입니다.
• x+= 업데이트는 Adagrad와 동일하지만 캐시 변수는 “누수”입니다.
• 따라서 RMSProp은 기울기의 크기를 기반으로 각 가중치의 학습률을 여전히 변조하는데, 이는 유익한 이퀄라이징 효과가 있지만 Adagrad와 달리 업데이트가 단조롭게 작아지지 않습니다.

Adam.
Adam is a recently proposed update that looks a bit like RMSProp with momentum.
The (simplified) update looks as follows:

• 아담.
• Adam은 모멘텀이 있는 RMSProp과 약간 비슷해 보이는 최근에 제안된 업데이트입니다.
• (단순화된) 업데이트는 다음과 같습니다.

m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)

Notice that the update looks exactly as RMSProp update, except the “smooth” version of the gradient m is used instead of the raw (and perhaps noisy) gradient vector dx.
Recommended values in the paper are eps = 1e-8, beta1 = 0.9, beta2 = 0.999.
In practice Adam is currently recommended as the default algorithm to use, and often works slightly better than RMSProp.
However, it is often also worth trying SGD+Nesterov Momentum as an alternative.
The full Adam update also includes a bias correction mechanism, which compensates for the fact that in the first few time steps the vectors m,v are both initialized and therefore biased at zero, before they fully “warm up”.
With the bias correction mechanism, the update looks as follows:

• 업데이트는 RMSProp 업데이트와 정확히 동일하지만, 원시(그리고 잡음이 많은) 그라디언트 벡터 dx 대신에 그라디언트 m의 “부드러운” 버전이 사용된다는 점에 유의하십시오.
• 논문에서 권장하는 값은 eps = 1e-8, beta1 = 0.9, beta2 = 0.999입니다.
• 실제로 Adam은 현재 사용할 기본 알고리즘으로 권장되며 종종 RMSProp보다 약간 더 잘 작동합니다.
• 그러나 종종 SGD+Nesterov Momentum을 대안으로 사용해 볼 가치가 있습니다.
• 전체 Adam 업데이트에는 바이어스 수정 메커니즘도 포함되어 있어 처음 몇 단계에서 벡터 m,v가 모두 초기화되어 완전히 “워밍업”되기 전에 0으로 바이어스된다는 사실을 보상합니다.
• 편향 수정 메커니즘을 사용하면 업데이트가 다음과 같이 표시됩니다.

# t is your iteration counter going from 1 to infinity
m = beta1*m + (1-beta1)*dx
mt = m / (1-beta1**t)
v = beta2*v + (1-beta2)*(dx**2)
vt = v / (1-beta2**t)
x += - learning_rate * mt / (np.sqrt(vt) + eps)

Note that the update is now a function of the iteration as well as the other parameters.
We refer the reader to the paper for the details, or the course slides where this is expanded on.

• 업데이트는 이제 다른 매개변수뿐만 아니라 반복의 함수입니다.
• 자세한 내용은 독자에게 논문을 참조하거나 이것이 확장되는 코스 슬라이드를 참조하십시오. Additional References:
• Unit Tests for Stochastic Optimization proposes a series of tests as a standardized benchmark for stochastic optimization.

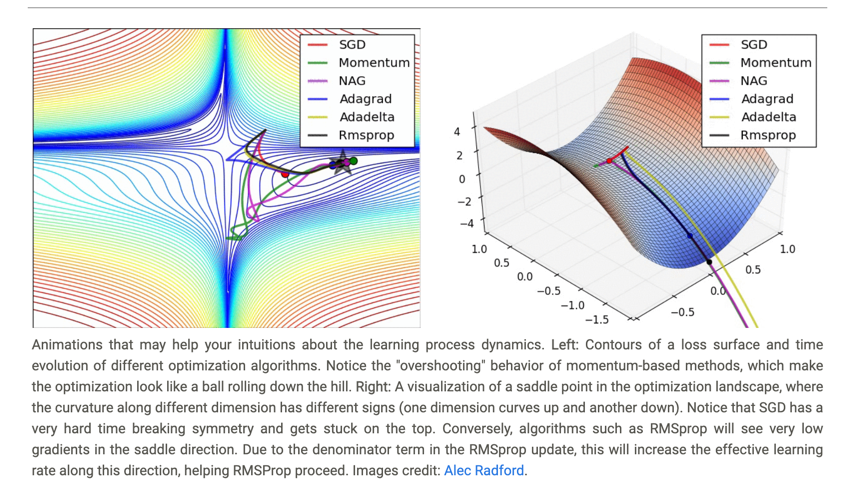
Animations that may help your intuitions about the learning process dynamics.
Left: Contours of a loss surface and time evolution of different optimization algorithms.
Notice the “overshooting” behavior of momentum-based methods, which make the optimization look like a ball rolling down the hill.
Right: A visualization of a saddle point in the optimization landscape, where the curvature along different dimension has different signs (one dimension curves up and another down).
Notice that SGD has a very hard time breaking symmetry and gets stuck on the top.
Conversely, algorithms such as RMSprop will see very low gradients in the saddle direction.
Due to the denominator term in the RMSprop update, this will increase the effective learning rate along this direction, helping RMSProp proceed. Images credit: Alec Radford.

• 학습 과정 역학에 대한 직관을 도울 수 있는 애니메이션.
• 왼쪽: 다양한 최적화 알고리즘의 손실 표면 윤곽 및 시간 변화.
• 최적화가 언덕 아래로 굴러가는 공처럼 보이게 만드는 모멘텀 기반 방법의 “오버슈팅” 동작에 주목하십시오.
• 오른쪽: 서로 다른 차원을 따라 곡률이 서로 다른 부호를 갖는 최적화 환경의 안장 지점 시각화(한 차원은 위로 휘고 다른 차원은 아래로 휘어짐).
• SGD는 대칭을 깨는 데 매우 어려움을 겪고 상단에 고정됩니다.
• 반대로 RMSprop과 같은 알고리즘은 안장 방향에서 매우 낮은 기울기를 볼 수 있습니다.
• RMSprop 업데이트의 분모 항으로 인해 이 방향을 따라 효과적인 학습 속도가 증가하여 RMSProp이 진행되는 데 도움이 됩니다. 이미지 제공: 알렉 래드포드.

5. Hyperparameter Optimization

As we’ve seen, training Neural Networks can involve many hyperparameter settings.
The most common hyperparameters in context of Neural Networks include:

• 우리가 본 것처럼 신경망 훈련에는 많은 하이퍼파라미터 설정이 포함될 수 있습니다.
• 신경망 맥락에서 가장 일반적인 하이퍼파라미터는 다음과 같습니다.

the initial learning rate
learning rate decay schedule (such as the decay constant)
regularization strength (L2 penalty, dropout strength)
But as we saw, there are many more relatively less sensitive hyperparameters, for example in per-parameter adaptive learning methods, the setting of momentum and its schedule, etc. In this section we describe some additional tips and tricks for performing the hyperparameter search:

• 초기 학습 속도
• 학습률 감소 일정(예: 감소 상수)
• 정규화 강도(L2 페널티, 드롭아웃 강도)
• 그러나 우리가 본 것처럼 예를 들어 매개변수별 적응 학습 방법, 모멘텀 및 일정 설정 등과 같이 상대적으로 덜 민감한 하이퍼 매개변수가 많이 있습니다. 이 섹션에서는 하이퍼 매개변수 검색을 수행하기 위한 몇 가지 추가 팁과 요령을 설명합니다.

Implementation. Larger Neural Networks typically require a long time to train, so performing hyperparameter search can take many days/weeks.
It is important to keep this in mind since it influences the design of your code base.
One particular design is to have a worker that continuously samples random hyperparameters and performs the optimization.
During the training, the worker will keep track of the validation performance after every epoch, and writes a model checkpoint (together with miscellaneous training statistics such as the loss over time) to a file, preferably on a shared file system.
It is useful to include the validation performance directly in the filename, so that it is simple to inspect and sort the progress.
Then there is a second program which we will call a master, which launches or kills workers across a computing cluster, and may additionally inspect the checkpoints written by workers and plot their training statistics, etc.

• 구현. 더 큰 신경망은 일반적으로 훈련하는 데 오랜 시간이 필요하므로 하이퍼파라미터 검색을 수행하는 데 며칠/몇 주가 걸릴 수 있습니다.
• 이것은 코드 기반의 디자인에 영향을 미치기 때문에 이를 염두에 두는 것이 중요합니다.
• 특정 디자인 중 하나는 무작위 하이퍼파라미터를 지속적으로 샘플링하고 최적화를 수행하는 작업자를 갖는 것입니다.
• 훈련하는 동안 작업자는 매 에포크 후 유효성 검사 성능을 추적하고 모델 체크포인트(시간 경과에 따른 손실과 같은 기타 훈련 통계와 함께)를 파일, 가급적이면 공유 파일 시스템에 기록합니다.
• 유효성 검사 성능을 파일 이름에 직접 포함하면 진행 상황을 검사하고 정렬하는 것이 간단해집니다.
• 그런 다음 마스터라고 부르는 두 번째 프로그램이 있습니다. 이 프로그램은 컴퓨팅 클러스터에서 작업자를 시작하거나 종료하고 추가로 작업자가 작성한 체크포인트를 검사하고 훈련 통계 등을 구성할 수 있습니다.

Prefer one validation fold to cross-validation.
In most cases a single validation set of respectable size substantially simplifies the code base, without the need for cross-validation with multiple folds.
You’ll hear people say they “cross-validated” a parameter, but many times it is assumed that they still only used a single validation set.

• 교차 검증보다 하나의 검증 접기를 선호하십시오.
• 대부분의 경우 상당한 크기의 단일 유효성 검사 세트는 여러 접기로 교차 유효성 검사를 수행할 필요 없이 코드 기반을 상당히 단순화합니다.
• 사람들이 매개변수를 “교차 검증”했다고 말하는 것을 들을 수 있지만, 여전히 단일 검증 세트만 사용했다고 가정하는 경우가 많습니다.

Hyperparameter ranges. Search for hyperparameters on log scale.
For example, a typical sampling of the learning rate would look as follows: learning_rate = 10 ** uniform(-6, 1).
That is, we are generating a random number from a uniform distribution, but then raising it to the power of 10. The same strategy should be used for the regularization strength.
Intuitively, this is because learning rate and regularization strength have multiplicative effects on the training dynamics.
For example, a fixed change of adding 0.01 to a learning rate has huge effects on the dynamics if the learning rate is 0.001, but nearly no effect if the learning rate when it is 10. This is because the learning rate multiplies the computed gradient in the update.
Therefore, it is much more natural to consider a range of learning rate multiplied or divided by some value, than a range of learning rate added or subtracted to by some value.
Some parameters (e.g. dropout) are instead usually searched in the original scale (e.g. dropout = uniform(0,1)).

• 하이퍼파라미터 범위. 로그 스케일에서 하이퍼파라미터를 검색합니다.
• 예를 들어 학습률의 일반적인 샘플링은 learning_rate = 10 ** uniform(-6, 1)과 같습니다.
• 즉, 균일한 분포에서 난수를 생성한 다음 10의 거듭제곱으로 올립니다. 정규화 강도에 동일한 전략을 사용해야 합니다.
• 직관적으로 이것은 학습 속도와 정규화 강도가 훈련 역학에 곱셈 효과를 갖기 때문입니다.
• 예를 들어 학습률에 0.01을 더하는 고정된 변화는 학습률이 0.001이면 역학에 큰 영향을 미치지만 학습률이 10일 때 거의 영향을 미치지 않습니다. 업데이트.
• 따라서 어떤 값을 더하거나 빼는 학습률의 범위보다 어떤 값을 곱하거나 나눈 학습률의 범위를 고려하는 것이 훨씬 더 자연스럽습니다.
• 대신 일부 매개변수(예: 드롭아웃)는 일반적으로 원래 스케일에서 검색됩니다(예: 드롭아웃 = uniform(0,1)).

Prefer random search to grid search.
As argued by Bergstra and Bengio in Random Search for Hyper-Parameter Optimization, “randomly chosen trials are more efficient for hyper-parameter optimization than trials on a grid”.
As it turns out, this is also usually easier to implement.

• 그리드 검색보다 임의 검색을 선호합니다.
• Hyper-Parameter Optimization을 위한 Random Search에서 Bergstra와 Bengio가 주장한 것처럼 “무작위로 선택한 시도는 그리드에서의 시도보다 하이퍼 매개변수 최적화에 더 효율적입니다.”
• 결과적으로 이것은 일반적으로 구현하기 더 쉽습니다.

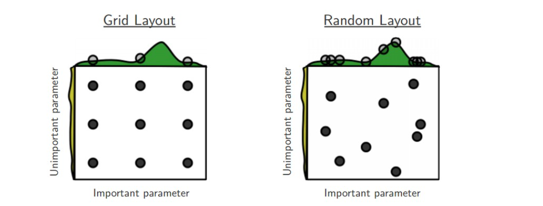
Core illustration from Random Search for Hyper-Parameter Optimization by Bergstra and Bengio.
It is very often the case that some of the hyperparameters matter much more than others (e.g. top hyperparam vs. left one in this figure).
Performing random search rather than grid search allows you to much more precisely discover good values for the important ones.

• Bergstra와 Bengio의 Hyper-Parameter Optimization을 위한 임의 검색의 핵심 일러스트레이션.
• 일부 하이퍼파라미터가 다른 하이퍼파라미터보다 훨씬 더 중요한 경우가 매우 많습니다(예: 상단 하이퍼파라미터 대 이 그림의 왼쪽 하이퍼파라미터).
• 그리드 검색이 아닌 임의 검색을 수행하면 중요한 값에 대한 좋은 값을 훨씬 더 정확하게 찾을 수 있습니다.

Careful with best values on border.
Sometimes it can happen that you’re searching for a hyperparameter (e.g. learning rate) in a bad range.
For example, suppose we use learning_rate = 10 ** uniform(-6, 1).
Once we receive the results, it is important to double check that the final learning rate is not at the edge of this interval, or otherwise you may be missing more optimal hyperparameter setting beyond the interval.

• 경계선에서 최고의 가치에 주의하십시오.
• 때로는 잘못된 범위에서 하이퍼파라미터(예: 학습률)를 검색하는 경우가 발생할 수 있습니다.
• 예를 들어 learning_rate = 10 ** uniform(-6, 1)을 사용한다고 가정합니다.
• 결과를 받으면 최종 학습 속도가 이 간격의 가장자리에 있지 않은지 다시 확인하는 것이 중요합니다. 그렇지 않으면 간격을 넘어서는 더 최적의 하이퍼파라미터 설정이 누락될 수 있습니다.

Stage your search from coarse to fine.
In practice, it can be helpful to first search in coarse ranges (e.g. 10 ** [-6, 1]), and then depending on where the best results are turning up, narrow the range.
Also, it can be helpful to perform the initial coarse search while only training for 1 epoch or even less, because many hyperparameter settings can lead the model to not learn at all, or immediately explode with infinite cost.
The second stage could then perform a narrower search with 5 epochs, and the last stage could perform a detailed search in the final range for many more epochs (for example).

• 대략적인 검색에서 정밀한 검색까지 단계적으로 진행하세요.
• 실제로는 대략적인 범위(예: 10 ** [-6, 1])에서 먼저 검색한 다음 최상의 결과가 나타나는 위치에 따라 범위를 좁히는 것이 도움이 될 수 있습니다.
• 또한 많은 하이퍼파라미터 설정으로 인해 모델이 전혀 학습하지 않거나 무한한 비용으로 즉시 폭발할 수 있기 때문에 1 epoch 또는 그 미만 동안만 훈련하는 동안 초기 대략적인 검색을 수행하는 것이 도움이 될 수 있습니다.
• 그런 다음 두 번째 단계는 5 epoch로 더 좁은 검색을 수행할 수 있고 마지막 단계는 더 많은 epoch(예:)에 대해 최종 범위에서 자세한 검색을 수행할 수 있습니다.

Bayesian Hyperparameter Optimization is a whole area of research devoted to coming up with algorithms that try to more efficiently navigate the space of hyperparameters.
The core idea is to appropriately balance the exploration - exploitation trade-off when querying the performance at different hyperparameters.
Multiple libraries have been developed based on these models as well, among some of the better known ones are Spearmint, SMAC, and Hyperopt.
However, in practical settings with ConvNets it is still relatively difficult to beat random search in a carefully-chosen intervals.
See some additional from-the-trenches discussion here.

• 베이지안 하이퍼파라미터 최적화는 하이퍼파라미터 공간을 보다 효율적으로 탐색하는 알고리즘을 제시하는 데 전념하는 전체 연구 영역입니다.
• 핵심 아이디어는 서로 다른 하이퍼파라미터에서 성능을 쿼리할 때 탐색-활용 트레이드오프의 균형을 적절하게 맞추는 것입니다.
• 이러한 모델을 기반으로 여러 라이브러리가 개발되었으며, 더 잘 알려진 라이브러리 중 일부는 Spearmint, SMAC 및 Hyperopt입니다.
• 그러나 ConvNet을 사용하는 실제 설정에서는 신중하게 선택한 간격에서 임의 검색을 능가하는 것이 여전히 상대적으로 어렵습니다.
• 여기에서 추가 참호 토론을 참조하십시오.

6. Evaluation

6.1 Model Ensembles

Model Ensembles
In practice, one reliable approach to improving the performance of Neural Networks by a few percent is to train multiple independent models, and at test time average their predictions.
As the number of models in the ensemble increases, the performance typically monotonically improves (though with diminishing returns).
Moreover, the improvements are more dramatic with higher model variety in the ensemble.
There are a few approaches to forming an ensemble:

• 모델 앙상블
• 실제로 신경망의 성능을 몇 퍼센트 향상시키는 한 가지 신뢰할 수 있는 접근 방식은 여러 독립 모델을 훈련하고 테스트 시간에 예측을 평균화하는 것입니다.
• 앙상블의 모델 수가 증가함에 따라 성능은 일반적으로 단조롭게 향상됩니다(수확 체감).
• 또한 앙상블의 모델 다양성이 높아짐에 따라 개선 사항이 더욱 극적으로 나타납니다.
• 앙상블을 구성하는 데는 몇 가지 접근 방식이 있습니다.

Same model, different initializations.
Use cross-validation to determine the best hyperparameters, then train multiple models with the best set of hyperparameters but with different random initialization.
The danger with this approach is that the variety is only due to initialization.

• 같은 모델, 다른 초기화.
• 교차 검증을 사용하여 최상의 하이퍼파라미터를 결정한 다음 최상의 하이퍼파라미터 세트로 여러 모델을 훈련하지만 다른 무작위 초기화를 사용합니다.
• 이 접근 방식의 위험은 다양성이 초기화 때문일 뿐이라는 것입니다.

Top models discovered during cross-validation.
Use cross-validation to determine the best hyperparameters, then pick the top few (e.g. 10) models to form the ensemble.
This improves the variety of the ensemble but has the danger of including suboptimal models.
In practice, this can be easier to perform since it doesn’t require additional retraining of models after cross-validation

• 교차 검증 중에 발견된 상위 모델.
• 교차 검증을 사용하여 최상의 하이퍼파라미터를 결정한 다음 상위 몇 개(예: 10개) 모델을 선택하여 앙상블을 형성합니다.
• 이렇게 하면 앙상블의 다양성이 향상되지만 최적이 아닌 모델을 포함할 위험이 있습니다.
• 실제로 교차 검증 후 모델을 추가로 재교육할 필요가 없기 때문에 이 작업을 더 쉽게 수행할 수 있습니다.

Different checkpoints of a single model.
If training is very expensive, some people have had limited success in taking different checkpoints of a single network over time (for example after every epoch) and using those to form an ensemble.
Clearly, this suffers from some lack of variety, but can still work reasonably well in practice.
The advantage of this approach is that is very cheap.

• 단일 모델의 다양한 체크포인트.
• 교육 비용이 매우 많이 드는 경우 일부 사람들은 시간이 지남에 따라(예: 모든 에포크 후) 단일 네트워크의 서로 다른 체크포인트를 선택하고 이를 사용하여 앙상블을 형성하는 데 제한적인 성공을 거두었습니다.
• 분명히 이것은 약간의 다양성 부족으로 어려움을 겪고 있지만 실제로는 여전히 합리적으로 잘 작동할 수 있습니다.
• 이 방법의 장점은 매우 저렴하다는 것입니다.

Running average of parameters during training.
Related to the last point, a cheap way of almost always getting an extra percent or two of performance is to maintain a second copy of the network’s weights in memory that maintains an exponentially decaying sum of previous weights during training.
This way you’re averaging the state of the network over last several iterations.
You will find that this “smoothed” version of the weights over last few steps almost always achieves better validation error.
The rough intuition to have in mind is that the objective is bowl-shaped and your network is jumping around the mode, so the average has a higher chance of being somewhere nearer the mode.

• 훈련 중 매개변수의 실행 평균입니다.
• 마지막 요점과 관련하여 거의 항상 성능의 추가 퍼센트 또는 2%를 얻는 저렴한 방법은 훈련 중에 이전 가중치의 기하급수적으로 감소하는 합계를 유지하는 메모리에 네트워크 가중치의 두 번째 복사본을 유지하는 것입니다.
• 이렇게 하면 마지막 몇 번의 반복에 걸쳐 네트워크 상태를 평균화할 수 있습니다.
• 마지막 몇 단계에 걸쳐 이 “평활한” 버전의 가중치가 거의 항상 더 나은 유효성 검사 오류를 달성한다는 것을 알게 될 것입니다.
• 염두에 두어야 할 대략적인 직관은 목표가 그릇 모양이고 네트워크가 모드 주위를 점프하므로 평균이 모드에 더 가까운 어딘가에 있을 가능성이 더 높다는 것입니다.

One disadvantage of model ensembles is that they take longer to evaluate on test example.
An interested reader may find the recent work from Geoff Hinton on “Dark Knowledge” inspiring, where the idea is to “distill” a good ensemble back to a single model by incorporating the ensemble log likelihoods into a modified objective.

• 모델 앙상블의 한 가지 단점은 테스트 예제에서 평가하는 데 더 오래 걸린다는 것입니다.
• 관심 있는 독자는 앙상블 로그 우도를 수정된 목표에 통합하여 좋은 앙상블을 다시 단일 모델로 “증류”하는 아이디어가 영감을 주는 “Dark Knowledge”에 대한 Geoff Hinton의 최근 작업을 찾을 수 있습니다.

7. Summary

To train a Neural Network:

Gradient check your implementation with a small batch of data and be aware of the pitfalls.

• 그라데이션은 소량의 데이터를 사용하여 구현을 확인하고 위험 요소를 인식합니다.

As a sanity check, make sure your initial loss is reasonable, and that you can achieve 100% training accuracy on a very small portion of the data

• 안전성 검사를 통해 초기 손실이 타당한지, 그리고 데이터의 아주 작은 부분에서 100% 교육 정확도를 달성할 수 있는지 확인합니다

During training, monitor the loss, the training/validation accuracy, and if you’re feeling fancier, the magnitude of updates in relation to parameter values (it should be ~1e-3), and when dealing with ConvNets, the first-layer weights.

• 교육 중에 손실, 교육/검증 정확도를 모니터링하고, 매개 변수 값과 관련된 업데이트의 크기(~1e-3이어야 함) 및 C를 처리할 때vNets의 첫 번째 계층 가중치.

The two recommended updates to use are either SGD+Nesterov Momentum or Adam.

• SGD+네스테로프 모멘텀 또는 Adam 두 가지 업데이트를 사용하는 것이 좋습니다.

Decay your learning rate over the period of the training. For example, halve the learning rate after a fixed number of epochs, or whenever the validation accuracy tops off.

• 교육 기간 동안 학습 속도를 저하시킵니다. 예를 들어, 고정된 에포크 수 이후 또는 유효성 검사 정확도가 떨어질 때마다 학습 속도를 절반으로 줄입니다.

Search for good hyperparameters with random search (not grid search). Stage your search from coarse (wide hyperparameter ranges, training only for 1-5 epochs), to fine (narrower rangers, training for many more epochs)

• 그리드 검색이 아닌 임의 검색으로 양호한 하이퍼 파라미터를 검색합니다. 대략적인 검색 단계(넓은 하이퍼파라미터 범위, 1-5 에포크 동안만 교육)에서 미세한 단계(좁은 레인저, 더 많은 에포크에 대한 교육)로 이동

Form model ensembles for extra performance

• 추가 성능을 위해 모델 앙상블 형성

8. Additional References

• SGD tips and tricks from Leon Bottou
  
• Efficient BackProp (pdf) from Yann LeCun
  
• Practical Recommendations for Gradient-Based Training of Deep Architectures from Yoshua Bengio
  

9. Additional references

• https://cs231n.github.io