cs231n & eecs498 Regularization and Optimization 교안 정리
0. Last Time : Loss function quantify preferences

- 총 2개의 분류 Loss Function 공부했음
- 하지만 Training data 결과가 좋지만, Test Data 결과가 안좋은것을 확인할 수 있음
- 이번 강의에서는 Training data를 가지고 Test Data 사용할 때 좋은 결과를 도출하는 알고리즘을 배움
1. Overfitting
- 위에 나오는 현상을 Overfitting(과적합) 이라고 정의됨
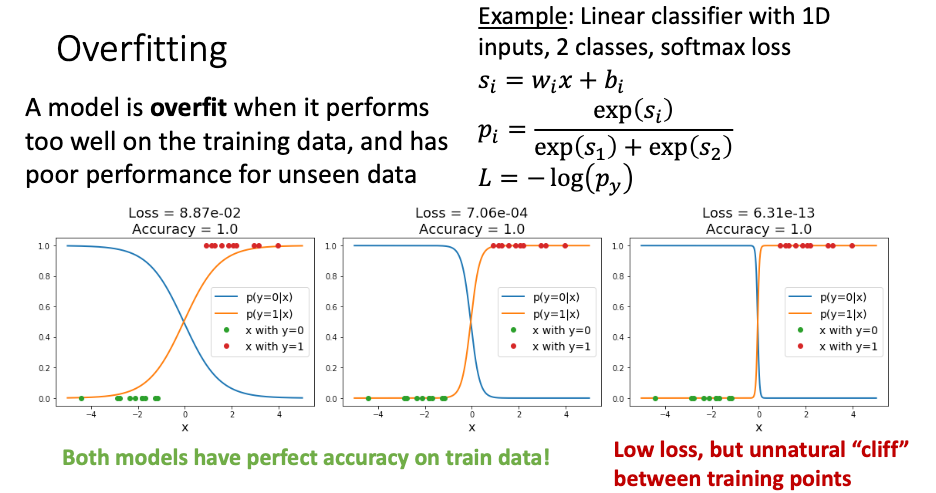
- 3개의 데이터 모두 overfit 경우라고 볼 수 있음
- loss 더 낮으면 과적합에 가깝다고 볼 수 있다.
2. Regularization : Beyond Training Error

- Loss 총 2개의 파트로 나눠짐
- data loss 실제로 훈련 도중에 data에서 나오는 loss 값
- Regularization data loss에 과적합을 방지하기 위한 값을 추가
- 방법으로는 L2, L1 방식으로 나눠짐
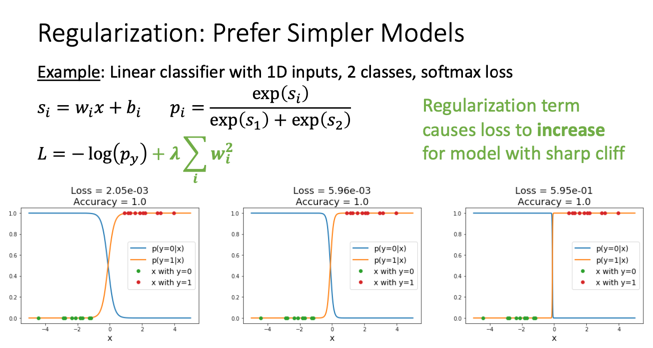
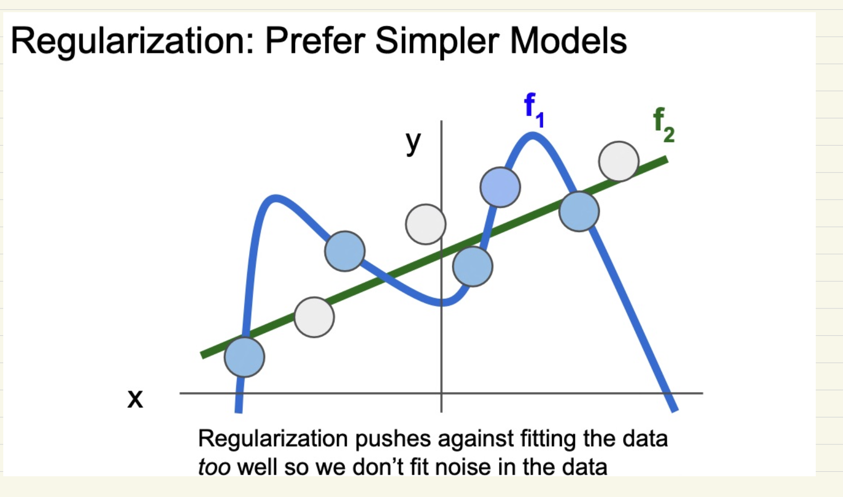
3. Finding a goog W

- Loss function은 총 data loss, regularization 구성되어 있음
- 그럼 최적에 Loss 값을 찾기 위해서는, W 값을 최적화 해야함
3.1 Random search
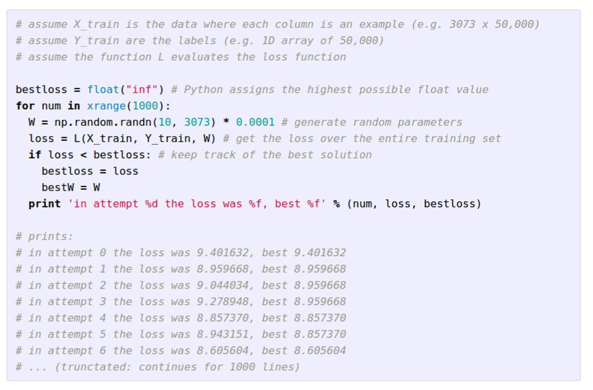
- 첫번째 방식으로는 W 값을 모두 랜덤으로 설정하는것
- 정말 좋지 못한 방법
3.2 Follow the slope

- 수학적 기법인 미분을 사용해 해당 W 최솟값을 찾아가는 과정
- 편미분을 활용해 최솟값을 찾아가는 과정
- 가장 가파르게 최소 점으로 가야한다.
3.2.1 Numeric Gradient

- 내가 가지고 있는 값에서 W 값을 0으로 수렴하도록 보내면, 미분 값을 얻일 수있다.
- 속도가 느리고, 구현하기 쉽다, 대략적인 값
3.2.2 Analytic gradient

- 속도가 빠르면, 정확한 값이지만 오류가 크다
- 근데 대부분 Analytic gradient 방식을 사용한다.
- 그리고 numeric gradient 방식은 체크하기 위해 같이 사용된다.
def eval_numerical_gradient(f, x, verbose=True, h=0.00001):
"""
a naive implementation of numerical gradient of f at x
- f should be a function that takes a single argument
- x is the point (numpy array) to evaluate the gradient at
"""
fx = f(x) # evaluate function value at original point
grad = np.zeros_like(x)
# iterate over all indexes in x
it = np.nditer(x, flags=["multi_index"], op_flags=["readwrite"])
while not it.finished:
# evaluate function at x+h
ix = it.multi_index
oldval = x[ix]
x[ix] = oldval + h # increment by h
fxph = f(x) # evalute f(x + h)
x[ix] = oldval - h
fxmh = f(x) # evaluate f(x - h)
x[ix] = oldval # restore
# compute the partial derivative with centered formula
grad[ix] = (fxph - fxmh) / (2 * h) # the slope
if verbose:
print(ix, grad[ix])
it.iternext() # step to next dimension
return grad
3.3 Computing Gradients



4 Gradient Descent
- Analytic gradient 사용하기 위해서는 Gradient Descent 개념을 알고 있어야 한다.
4.1 GD(Gradient Descent)
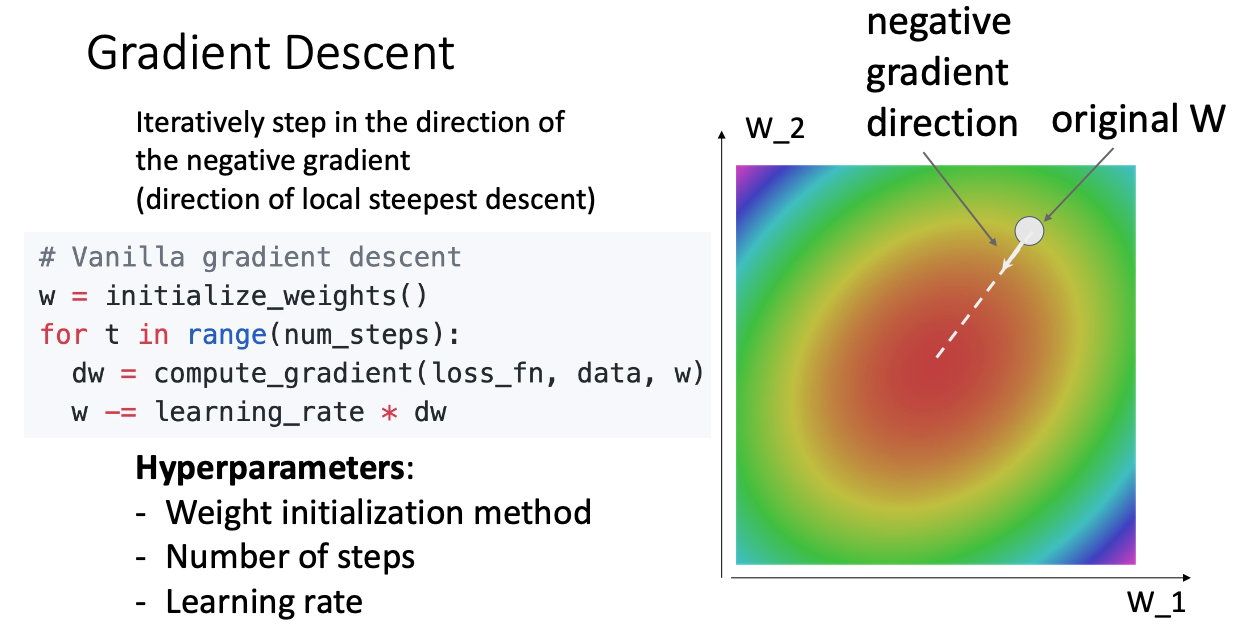
- W 값을 최적에 편미분을 활용해 값이 제일 낮은 곳으로 가게 하는 방식이다.
- Hyperparameter 가중치 초기화, LR, Step 존재한다.
4.2 BGD(Batch Gradient Descent)
- 한번에 처리하기 힘드니까 Batch 사이즈를 조절해 훈련한다.
4.3 SGD(Stochastic Gradient Descent)

- 배치 사이즈를 너무 크게 설정하는 것이 아니라 조금만 배치 사이즈(32, 64, 128) 사용해 학습을 진행한다.
- Batch Size, Data Sampling
4.3.1 SGD Problems
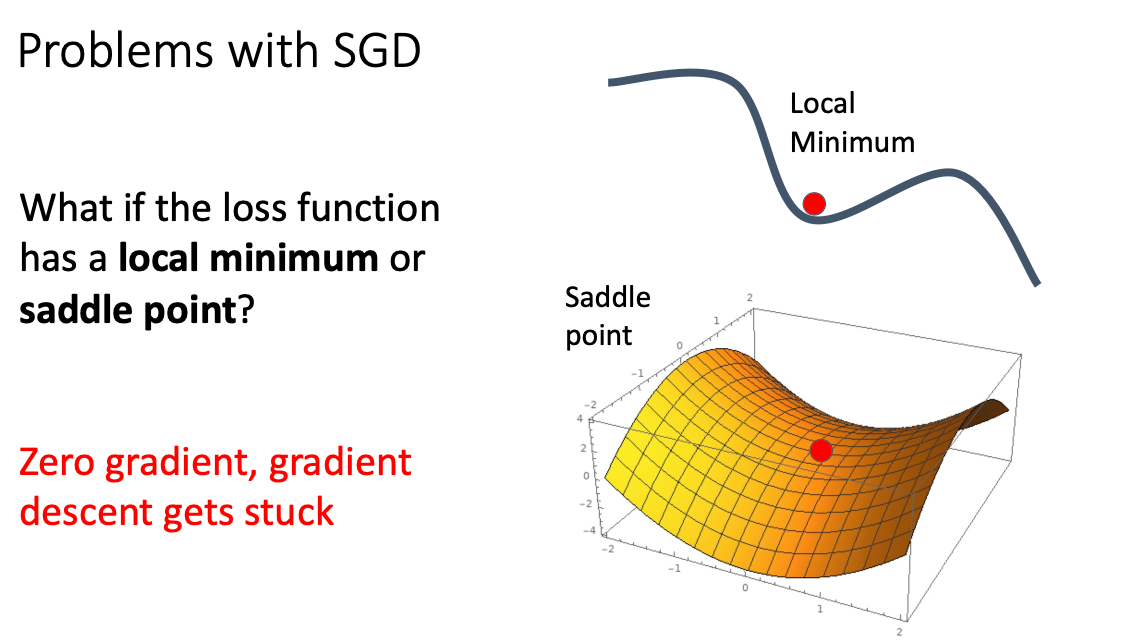
- 값이 앏은 곳을 지나갈 때는 매우 느리게 지행되고, 가파른 방향을 가게 된다면 급격하게 가게 딘다.
- Local Minimum 현상이 발생할 수 있다. 기울기 값이 0이라면 거기서 Update 진행되지 않고 머물러 지는 현상이다.
- Local Minimum 방지하기 위해서는 가속도를 주면 0에 머물러 있지 않고 앞으로 간다!
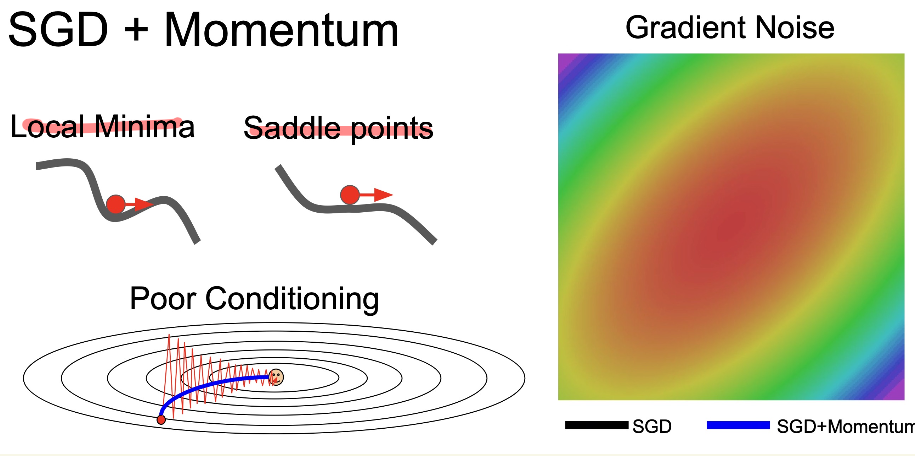
5. SGD + Momentum
- Local Minimum 해결방법 가속도를 이용해 앞으로 전진하게 된다.

- 두개는 같은 수식이다
- 일정한 기울기가 있는 방향으로 속도를 증가 시킴
- v velocity : 가속도
- rho : 마찰계수 0.9 or 0.99 사용 (급발진 예방)
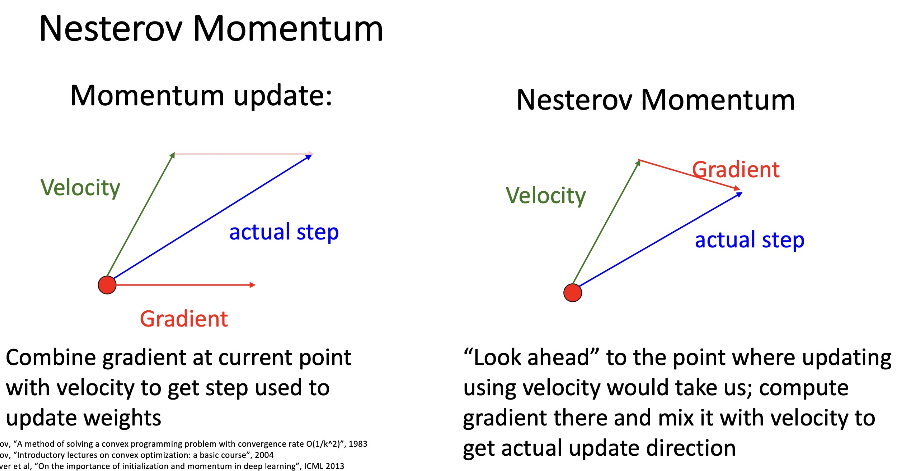
6. Nesterov Momentum
7. AdaGrad

- 위에서는 학습 속도 상관없이 훈련하는 방법
- 이번 AdaGrad, Adam etc 학습 속도를 맞춤으로 학습 속도
- grad_squared 제곱하고 루트를 적용해 나눔으로서 lr 맞춤으로 조절
- 만약 값이 크면, 속도를 늦추고 값이 작으면 가속도가 붙는다.
8. RMSProp

- 단순하게 decay_rate 비율를 추가해 속드를 조절하게 된다.
9.Adam

- 대부분 많이 사용하는 기법
-
10. L2 Regularization vs Weight Decay


Additional references
- https://cs231n.github.io
- https://web.eecs.umich.edu/~justincj/teaching/eecs498/WI2022/schedule.html